CINXE.COM

<!doctype html> <html class=""> <head> <meta charset="utf-8" /> <meta name="viewport" content="width=device-width, initial-scale=1.0, user-scalable=no" /> <meta name="description" content="We’re on a journey to advance and democratize artificial intelligence through open source and open science." /> <meta property="fb:app_id" content="1321688464574422" /> <meta name="twitter:card" content="summary_large_image" /> <meta name="twitter:site" content="@huggingface" /> <meta name="twitter:image" content="https://cdn-thumbnails.huggingface.co/social-thumbnails/datasets/AI-MO/NuminaMath-1.5.png" /> <meta property="og:title" content="AI-MO/NuminaMath-1.5 · Datasets at Hugging Face" /> <meta property="og:type" content="website" /> <meta property="og:url" content="https://huggingface.co/datasets/AI-MO/NuminaMath-1.5" /> <meta property="og:image" content="https://cdn-thumbnails.huggingface.co/social-thumbnails/datasets/AI-MO/NuminaMath-1.5.png" /> <link rel="stylesheet" href="/front/build/kube-b666922/style.css" /> <link rel="preconnect" href="https://fonts.gstatic.com" /> <link href="https://fonts.googleapis.com/css2?family=Source+Sans+Pro:ital,wght@0,200;0,300;0,400;0,600;0,700;0,900;1,200;1,300;1,400;1,600;1,700;1,900&display=swap" rel="stylesheet" /> <link href="https://fonts.googleapis.com/css2?family=IBM+Plex+Mono:wght@400;600;700&display=swap" rel="stylesheet" /> <link rel="preload" href="https://cdnjs.cloudflare.com/ajax/libs/KaTeX/0.12.0/katex.min.css" as="style" onload="this.onload=null;this.rel='stylesheet'" /> <noscript> <link rel="stylesheet" href="https://cdnjs.cloudflare.com/ajax/libs/KaTeX/0.12.0/katex.min.css" /> </noscript> <script>const guestTheme = document.cookie.match(/theme=(\w+)/)?.[1]; document.documentElement.classList.toggle('dark', guestTheme === 'dark' || ( (!guestTheme || guestTheme === 'system') && window.matchMedia('(prefers-color-scheme: dark)').matches));</script> <link rel="canonical" href="https://huggingface.co/datasets/AI-MO/NuminaMath-1.5"> <script type="application/ld+json">{ "@context": { "@language": "en", "@vocab": "https:\/\/schema.org\/", "citeAs": "cr:citeAs", "column": "cr:column", "conformsTo": "dct:conformsTo", "cr": "http:\/\/mlcommons.org\/croissant\/", "data": { "@id": "cr:data", "@type": "@json" }, "dataBiases": "cr:dataBiases", "dataCollection": "cr:dataCollection", "dataType": { "@id": "cr:dataType", "@type": "@vocab" }, "dct": "http:\/\/purl.org\/dc\/terms\/", "extract": "cr:extract", "field": "cr:field", "fileProperty": "cr:fileProperty", "fileObject": "cr:fileObject", "fileSet": "cr:fileSet", "format": "cr:format", "includes": "cr:includes", "isLiveDataset": "cr:isLiveDataset", "jsonPath": "cr:jsonPath", "key": "cr:key", "md5": "cr:md5", "parentField": "cr:parentField", "path": "cr:path", "personalSensitiveInformation": "cr:personalSensitiveInformation", "recordSet": "cr:recordSet", "references": "cr:references", "regex": "cr:regex", "repeated": "cr:repeated", "replace": "cr:replace", "sc": "https:\/\/schema.org\/", "separator": "cr:separator", "source": "cr:source", "subField": "cr:subField", "transform": "cr:transform" }, "@type": "sc:Dataset", "distribution": [ { "@type": "cr:FileObject", "@id": "repo", "name": "repo", "description": "The Hugging Face git repository.", "contentUrl": "https:\/\/huggingface.co\/datasets\/AI-MO\/NuminaMath-1.5\/tree\/refs%2Fconvert%2Fparquet", "encodingFormat": "git+https", "sha256": "https:\/\/github.com\/mlcommons\/croissant\/issues\/80" }, { "@type": "cr:FileSet", "@id": "parquet-files-for-config-default", "containedIn": { "@id": "repo" }, "encodingFormat": "application\/x-parquet", "includes": "default\/*\/*.parquet" } ], "recordSet": [ { "@type": "cr:RecordSet", "dataType": "cr:Split", "key": { "@id": "default_splits\/split_name" }, "@id": "default_splits", "name": "default_splits", "description": "Splits for the default config.", "field": [ { "@type": "cr:Field", "@id": "default_splits\/split_name", "dataType": "sc:Text" } ], "data": [ { "default_splits\/split_name": "train" } ] }, { "@type": "cr:RecordSet", "@id": "default", "description": "AI-MO\/NuminaMath-1.5 - 'default' subset", "field": [ { "@type": "cr:Field", "@id": "default\/split", "dataType": "sc:Text", "source": { "fileSet": { "@id": "parquet-files-for-config-default" }, "extract": { "fileProperty": "fullpath" }, "transform": { "regex": "default\/(?:partial-)?(train)\/.+parquet$" } }, "references": { "field": { "@id": "default_splits\/split_name" } } }, { "@type": "cr:Field", "@id": "default\/problem", "dataType": "sc:Text", "source": { "fileSet": { "@id": "parquet-files-for-config-default" }, "extract": { "column": "problem" } } }, { "@type": "cr:Field", "@id": "default\/solution", "dataType": "sc:Text", "source": { "fileSet": { "@id": "parquet-files-for-config-default" }, "extract": { "column": "solution" } } }, { "@type": "cr:Field", "@id": "default\/answer", "dataType": "sc:Text", "source": { "fileSet": { "@id": "parquet-files-for-config-default" }, "extract": { "column": "answer" } } }, { "@type": "cr:Field", "@id": "default\/problem_type", "dataType": "sc:Text", "source": { "fileSet": { "@id": "parquet-files-for-config-default" }, "extract": { "column": "problem_type" } } }, { "@type": "cr:Field", "@id": "default\/question_type", "dataType": "sc:Text", "source": { "fileSet": { "@id": "parquet-files-for-config-default" }, "extract": { "column": "question_type" } } }, { "@type": "cr:Field", "@id": "default\/problem_is_valid", "dataType": "sc:Text", "source": { "fileSet": { "@id": "parquet-files-for-config-default" }, "extract": { "column": "problem_is_valid" } } }, { "@type": "cr:Field", "@id": "default\/solution_is_valid", "dataType": "sc:Text", "source": { "fileSet": { "@id": "parquet-files-for-config-default" }, "extract": { "column": "solution_is_valid" } } }, { "@type": "cr:Field", "@id": "default\/source", "dataType": "sc:Text", "source": { "fileSet": { "@id": "parquet-files-for-config-default" }, "extract": { "column": "source" } } }, { "@type": "cr:Field", "@id": "default\/synthetic", "dataType": "sc:Boolean", "source": { "fileSet": { "@id": "parquet-files-for-config-default" }, "extract": { "column": "synthetic" } } } ] } ], "conformsTo": "http:\/\/mlcommons.org\/croissant\/1.0", "name": "NuminaMath-1.5", "description": "\n\t\n\t\t\n\t\tDataset Card for NuminaMath 1.5\n\t\n\n\n\t\n\t\t\n\t\tDataset Summary\n\t\n\nThis is the second iteration of the popular NuminaMath dataset, bringing high quality post-training data for approximately 900k competition-level math problems. Each solution is formatted in a Chain of Thought (CoT) manner. The sources of the dataset range from Chinese high school math exercises to US and international mathematics olympiad competition problems. The data were primarily collected from online exam paper PDFs… See the full description on the dataset page: https:\/\/huggingface.co\/datasets\/AI-MO\/NuminaMath-1.5.", "alternateName": [ "AI-MO\/NuminaMath-1.5", "NuminaMath 1.5" ], "creator": { "@type": "Organization", "name": "Project-Numina", "url": "https:\/\/huggingface.co\/AI-MO" }, "keywords": [ "text-generation", "English", "apache-2.0", "100K - 1M", "parquet", "Text", "Datasets", "Dask", "Croissant", "Polars", "🇺🇸 Region: US", "math", "post-training" ], "license": "https:\/\/choosealicense.com\/licenses\/apache-2.0\/", "sameAs": "https:\/\/projectnumina.ai", "url": "https:\/\/huggingface.co\/datasets\/AI-MO\/NuminaMath-1.5" }</script> <title>AI-MO/NuminaMath-1.5 · Datasets at Hugging Face</title> <script defer data-domain="huggingface.co" event-loggedIn="false" src="/js/script.pageview-props.js" ></script> <script> window.plausible = window.plausible || function () { (window.plausible.q = window.plausible.q || []).push(arguments); }; </script> <script> window.hubConfig = {"features":{"signupDisabled":false},"sshGitUrl":"git@hf.co","moonHttpUrl":"https:\/\/huggingface.co","captchaApiKey":"bd5f2066-93dc-4bdd-a64b-a24646ca3859","captchaDisabledOnSignup":true,"datasetViewerPublicUrl":"https:\/\/datasets-server.huggingface.co","stripePublicKey":"pk_live_x2tdjFXBCvXo2FFmMybezpeM00J6gPCAAc","environment":"production","userAgent":"HuggingFace (production)","spacesIframeDomain":"hf.space","spacesApiUrl":"https:\/\/api.hf.space","docSearchKey":"ece5e02e57300e17d152c08056145326e90c4bff3dd07d7d1ae40cf1c8d39cb6","logoDev":{"apiUrl":"https:\/\/img.logo.dev\/","apiKey":"pk_UHS2HZOeRnaSOdDp7jbd5w"}}; </script> <script type="text/javascript" src="https://de5282c3ca0c.edge.sdk.awswaf.com/de5282c3ca0c/526cf06acb0d/challenge.js" defer></script> </head> <body class="flex flex-col min-h-dvh bg-white dark:bg-gray-950 text-black DatasetPage"> <div class="flex min-h-dvh flex-col"><div class="SVELTE_HYDRATER contents" data-target="SystemThemeMonitor" data-props="{"isLoggedIn":false}"></div> <div class="SVELTE_HYDRATER contents" data-target="MainHeader" data-props="{"classNames":"","isWide":false,"isZh":false,"isPro":false}"><header class="border-b border-gray-100 "><div class="w-full px-4 container flex h-16 items-center"><div class="flex flex-1 items-center"><a class="mr-5 flex flex-none items-center lg:mr-6" href="/"><img alt="Hugging Face's logo" class="w-7 md:mr-2" src="/front/assets/huggingface_logo-noborder.svg"> <span class="hidden whitespace-nowrap text-lg font-bold md:block">Hugging Face</span></a> <div class="relative flex-1 lg:max-w-sm mr-2 sm:mr-4 md:mr-3 xl:mr-6"><input autocomplete="off" class="w-full dark:bg-gray-950 pl-8 form-input-alt h-9 pr-3 focus:shadow-xl " name="" placeholder="Search models, datasets, users..." spellcheck="false" type="text" value=""> <svg class="absolute left-2.5 text-gray-400 top-1/2 transform -translate-y-1/2" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32"><path d="M30 28.59L22.45 21A11 11 0 1 0 21 22.45L28.59 30zM5 14a9 9 0 1 1 9 9a9 9 0 0 1-9-9z" fill="currentColor"></path></svg> </div> <div class="flex flex-none items-center justify-center p-0.5 place-self-stretch lg:hidden"><button class="relative z-40 flex h-6 w-8 items-center justify-center" type="button"><svg width="1em" height="1em" viewBox="0 0 10 10" class="text-xl" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" preserveAspectRatio="xMidYMid meet" fill="currentColor"><path fill-rule="evenodd" clip-rule="evenodd" d="M1.65039 2.9999C1.65039 2.8066 1.80709 2.6499 2.00039 2.6499H8.00039C8.19369 2.6499 8.35039 2.8066 8.35039 2.9999C8.35039 3.1932 8.19369 3.3499 8.00039 3.3499H2.00039C1.80709 3.3499 1.65039 3.1932 1.65039 2.9999ZM1.65039 4.9999C1.65039 4.8066 1.80709 4.6499 2.00039 4.6499H8.00039C8.19369 4.6499 8.35039 4.8066 8.35039 4.9999C8.35039 5.1932 8.19369 5.3499 8.00039 5.3499H2.00039C1.80709 5.3499 1.65039 5.1932 1.65039 4.9999ZM2.00039 6.6499C1.80709 6.6499 1.65039 6.8066 1.65039 6.9999C1.65039 7.1932 1.80709 7.3499 2.00039 7.3499H8.00039C8.19369 7.3499 8.35039 7.1932 8.35039 6.9999C8.35039 6.8066 8.19369 6.6499 8.00039 6.6499H2.00039Z"></path></svg> </button> </div></div> <nav aria-label="Main" class="ml-auto hidden lg:block"><ul class="flex items-center space-x-1.5 2xl:space-x-2"><li class="hover:text-indigo-700"><a class="group flex items-center px-2 py-0.5 dark:text-gray-300 dark:hover:text-gray-100" href="/models"><svg class="mr-1.5 text-gray-400 group-hover:text-indigo-500" style="" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 24 24"><path class="uim-quaternary" d="M20.23 7.24L12 12L3.77 7.24a1.98 1.98 0 0 1 .7-.71L11 2.76c.62-.35 1.38-.35 2 0l6.53 3.77c.29.173.531.418.7.71z" opacity=".25" fill="currentColor"></path><path class="uim-tertiary" d="M12 12v9.5a2.09 2.09 0 0 1-.91-.21L4.5 17.48a2.003 2.003 0 0 1-1-1.73v-7.5a2.06 2.06 0 0 1 .27-1.01L12 12z" opacity=".5" fill="currentColor"></path><path class="uim-primary" d="M20.5 8.25v7.5a2.003 2.003 0 0 1-1 1.73l-6.62 3.82c-.275.13-.576.198-.88.2V12l8.23-4.76c.175.308.268.656.27 1.01z" fill="currentColor"></path></svg> Models</a> </li><li class="hover:text-red-700"><a class="group flex items-center px-2 py-0.5 dark:text-gray-300 dark:hover:text-gray-100" href="/datasets"><svg class="mr-1.5 text-gray-400 group-hover:text-red-500" style="" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 25 25"><ellipse cx="12.5" cy="5" fill="currentColor" fill-opacity="0.25" rx="7.5" ry="2"></ellipse><path d="M12.5 15C16.6421 15 20 14.1046 20 13V20C20 21.1046 16.6421 22 12.5 22C8.35786 22 5 21.1046 5 20V13C5 14.1046 8.35786 15 12.5 15Z" fill="currentColor" opacity="0.5"></path><path d="M12.5 7C16.6421 7 20 6.10457 20 5V11.5C20 12.6046 16.6421 13.5 12.5 13.5C8.35786 13.5 5 12.6046 5 11.5V5C5 6.10457 8.35786 7 12.5 7Z" fill="currentColor" opacity="0.5"></path><path d="M5.23628 12C5.08204 12.1598 5 12.8273 5 13C5 14.1046 8.35786 15 12.5 15C16.6421 15 20 14.1046 20 13C20 12.8273 19.918 12.1598 19.7637 12C18.9311 12.8626 15.9947 13.5 12.5 13.5C9.0053 13.5 6.06886 12.8626 5.23628 12Z" fill="currentColor"></path></svg> Datasets</a> </li><li class="hover:text-blue-700"><a class="group flex items-center px-2 py-0.5 dark:text-gray-300 dark:hover:text-gray-100" href="/spaces"><svg class="mr-1.5 text-gray-400 group-hover:text-blue-500" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" viewBox="0 0 25 25"><path opacity=".5" d="M6.016 14.674v4.31h4.31v-4.31h-4.31ZM14.674 14.674v4.31h4.31v-4.31h-4.31ZM6.016 6.016v4.31h4.31v-4.31h-4.31Z" fill="currentColor"></path><path opacity=".75" fill-rule="evenodd" clip-rule="evenodd" d="M3 4.914C3 3.857 3.857 3 4.914 3h6.514c.884 0 1.628.6 1.848 1.414a5.171 5.171 0 0 1 7.31 7.31c.815.22 1.414.964 1.414 1.848v6.514A1.914 1.914 0 0 1 20.086 22H4.914A1.914 1.914 0 0 1 3 20.086V4.914Zm3.016 1.102v4.31h4.31v-4.31h-4.31Zm0 12.968v-4.31h4.31v4.31h-4.31Zm8.658 0v-4.31h4.31v4.31h-4.31Zm0-10.813a2.155 2.155 0 1 1 4.31 0 2.155 2.155 0 0 1-4.31 0Z" fill="currentColor"></path><path opacity=".25" d="M16.829 6.016a2.155 2.155 0 1 0 0 4.31 2.155 2.155 0 0 0 0-4.31Z" fill="currentColor"></path></svg> Spaces</a> </li><li class="hover:text-yellow-700 max-xl:hidden"><a class="group flex items-center px-2 py-0.5 dark:text-gray-300 dark:hover:text-gray-100" href="/posts"><svg class="mr-1.5 text-gray-400 group-hover:text-yellow-500 !text-yellow-500" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" viewBox="0 0 12 12" preserveAspectRatio="xMidYMid meet"><path fill="currentColor" fill-rule="evenodd" d="M3.73 2.4A4.25 4.25 0 1 1 6 10.26H2.17l-.13-.02a.43.43 0 0 1-.3-.43l.01-.06a.43.43 0 0 1 .12-.22l.84-.84A4.26 4.26 0 0 1 3.73 2.4Z" clip-rule="evenodd"></path></svg> Posts</a> </li><li class="hover:text-yellow-700"><a class="group flex items-center px-2 py-0.5 dark:text-gray-300 dark:hover:text-gray-100" href="/docs"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" role="img" class="mr-1.5 text-gray-400 group-hover:text-yellow-500" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 16 16"><path d="m2.28 3.7-.3.16a.67.67 0 0 0-.34.58v8.73l.01.04.02.07.01.04.03.06.02.04.02.03.04.06.05.05.04.04.06.04.06.04.08.04.08.02h.05l.07.02h.11l.04-.01.07-.02.03-.01.07-.03.22-.12a5.33 5.33 0 0 1 5.15.1.67.67 0 0 0 .66 0 5.33 5.33 0 0 1 5.33 0 .67.67 0 0 0 1-.58V4.36a.67.67 0 0 0-.34-.5l-.3-.17v7.78a.63.63 0 0 1-.87.59 4.9 4.9 0 0 0-4.35.35l-.65.39a.29.29 0 0 1-.15.04.29.29 0 0 1-.16-.04l-.65-.4a4.9 4.9 0 0 0-4.34-.34.63.63 0 0 1-.87-.59V3.7Z" fill="currentColor" class="dark:opacity-40"></path><path fill-rule="evenodd" clip-rule="evenodd" d="M8 3.1a5.99 5.99 0 0 0-5.3-.43.66.66 0 0 0-.42.62v8.18c0 .45.46.76.87.59a4.9 4.9 0 0 1 4.34.35l.65.39c.05.03.1.04.16.04.05 0 .1-.01.15-.04l.65-.4a4.9 4.9 0 0 1 4.35-.34.63.63 0 0 0 .86-.59V3.3a.67.67 0 0 0-.41-.62 5.99 5.99 0 0 0-5.3.43l-.3.17L8 3.1Zm.73 1.87a.43.43 0 1 0-.86 0v5.48a.43.43 0 0 0 .86 0V4.97Z" fill="currentColor" class="opacity-40 dark:opacity-100"></path><path d="M8.73 4.97a.43.43 0 1 0-.86 0v5.48a.43.43 0 1 0 .86 0V4.96Z" fill="currentColor" class="dark:opacity-40"></path></svg> Docs</a> </li><li class="hover:text-green-700"><a class="group flex items-center px-2 py-0.5 dark:text-gray-300 dark:hover:text-gray-100" href="/enterprise"><svg class="mr-1.5 text-gray-400 group-hover:text-green-500" xmlns="http://www.w3.org/2000/svg" fill="none" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 33 27"><path fill="currentColor" fill-rule="evenodd" d="M13.5.7a8.7 8.7 0 0 0-7.7 5.7L1 20.6c-1 3.1.9 5.7 4.1 5.7h15c3.3 0 6.8-2.6 7.8-5.7l4.6-14.2c1-3.1-.8-5.7-4-5.7h-15Zm1.1 5.7L9.8 20.3h9.8l1-3.1h-5.8l.8-2.5h4.8l1.1-3h-4.8l.8-2.3H23l1-3h-9.5Z" clip-rule="evenodd"></path></svg> Enterprise</a> </li> <li><a class="group flex items-center px-2 py-0.5 dark:text-gray-300 dark:hover:text-gray-100" href="/pricing">Pricing </a></li> <li><div class="relative group"> <button class="px-2 py-0.5 hover:text-gray-500 dark:hover:text-gray-600 flex items-center " type="button"> <svg class=" text-gray-500 w-5 group-hover:text-gray-400 dark:text-gray-300 dark:group-hover:text-gray-100" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" viewBox="0 0 32 18" preserveAspectRatio="xMidYMid meet"><path fill-rule="evenodd" clip-rule="evenodd" d="M14.4504 3.30221C14.4504 2.836 14.8284 2.45807 15.2946 2.45807H28.4933C28.9595 2.45807 29.3374 2.836 29.3374 3.30221C29.3374 3.76842 28.9595 4.14635 28.4933 4.14635H15.2946C14.8284 4.14635 14.4504 3.76842 14.4504 3.30221Z" fill="currentColor"></path><path fill-rule="evenodd" clip-rule="evenodd" d="M14.4504 9.00002C14.4504 8.53382 14.8284 8.15588 15.2946 8.15588H28.4933C28.9595 8.15588 29.3374 8.53382 29.3374 9.00002C29.3374 9.46623 28.9595 9.84417 28.4933 9.84417H15.2946C14.8284 9.84417 14.4504 9.46623 14.4504 9.00002Z" fill="currentColor"></path><path fill-rule="evenodd" clip-rule="evenodd" d="M14.4504 14.6978C14.4504 14.2316 14.8284 13.8537 15.2946 13.8537H28.4933C28.9595 13.8537 29.3374 14.2316 29.3374 14.6978C29.3374 15.164 28.9595 15.542 28.4933 15.542H15.2946C14.8284 15.542 14.4504 15.164 14.4504 14.6978Z" fill="currentColor"></path><path fill-rule="evenodd" clip-rule="evenodd" d="M1.94549 6.87377C2.27514 6.54411 2.80962 6.54411 3.13928 6.87377L6.23458 9.96907L9.32988 6.87377C9.65954 6.54411 10.194 6.54411 10.5237 6.87377C10.8533 7.20343 10.8533 7.73791 10.5237 8.06756L6.23458 12.3567L1.94549 8.06756C1.61583 7.73791 1.61583 7.20343 1.94549 6.87377Z" fill="currentColor"></path></svg> </button> </div></li> <li><hr class="h-5 w-0.5 border-none bg-gray-100 dark:bg-gray-800"></li> <li><a class="block cursor-pointer whitespace-nowrap px-2 py-0.5 hover:text-gray-500 dark:text-gray-300 dark:hover:text-gray-100" href="/login">Log In </a></li> <li><a class="whitespace-nowrap rounded-full border border-transparent bg-gray-900 px-3 py-1 leading-none text-white hover:border-black hover:bg-white hover:text-black" href="/join">Sign Up </a></li></ul></nav></div></header></div> <div class="SVELTE_HYDRATER contents" data-target="SSOBanner" data-props="{}"></div> <main class="flex flex-1 flex-col"> <div class="SVELTE_HYDRATER contents" data-target="DatasetHeader" data-props="{"activeTab":"datasetCard","author":{"avatarUrl":"https://cdn-avatars.huggingface.co/v1/production/uploads/661d3f3e85f70e208d6f20db/kaXbnZDekN1gPzmRG_aFV.png","fullname":"Project-Numina","name":"AI-MO","type":"org","isHf":false,"isMod":false,"isEnterprise":true,"followerCount":248},"canReadRepoSettings":false,"dataset":{"author":"AI-MO","cardData":{"license":"apache-2.0","task_categories":["text-generation"],"language":["en"],"tags":["math","post-training"],"pretty_name":"NuminaMath 1.5"},"cardExists":true,"createdAt":"2025-02-10T12:34:15.000Z","description":"\n\t\n\t\t\n\t\tDataset Card for NuminaMath 1.5\n\t\n\n\n\t\n\t\t\n\t\tDataset Summary\n\t\n\nThis is the second iteration of the popular NuminaMath dataset, bringing high quality post-training data for approximately 900k competition-level math problems. Each solution is formatted in a Chain of Thought (CoT) manner. The sources of the dataset range from Chinese high school math exercises to US and international mathematics olympiad competition problems. The data were primarily collected from online exam paper PDFs… See the full description on the dataset page: https://huggingface.co/datasets/AI-MO/NuminaMath-1.5.","downloads":1853,"downloadsAllTime":1853,"id":"AI-MO/NuminaMath-1.5","isLikedByUser":false,"lastModified":"2025-02-10T13:28:01.000Z","likes":106,"datasetsServerInfo":{"viewer":"viewer","numRows":896215,"libraries":["datasets","dask","mlcroissant","polars"],"formats":["parquet"],"modalities":["text"]},"discussionsDisabled":false,"repoType":"dataset","private":false,"gated":false,"tags":["task_categories:text-generation","language:en","license:apache-2.0","size_categories:100K<n<1M","format:parquet","modality:text","library:datasets","library:dask","library:mlcroissant","library:polars","region:us","math","post-training"],"tag_objs":[{"id":"task_categories:text-generation","label":"text-generation","type":"task_categories","subType":"nlp"},{"id":"language:en","label":"English","type":"language"},{"id":"license:apache-2.0","label":"apache-2.0","type":"license"},{"id":"size_categories:100K<n<1M","label":"100K - 1M","type":"size_categories"},{"id":"format:parquet","label":"parquet","type":"format"},{"id":"modality:text","label":"Text","type":"modality"},{"id":"library:datasets","label":"Datasets","type":"library"},{"id":"library:dask","label":"Dask","type":"library"},{"id":"library:mlcroissant","label":"Croissant","type":"library"},{"id":"library:polars","label":"Polars","type":"library"},{"type":"region","label":"🇺🇸 Region: US","id":"region:us"},{"id":"math","label":"math","type":"other"},{"id":"post-training","label":"post-training","type":"other"}],"homepage":"https://projectnumina.ai","hasBlockedOids":false,"region":"us"},"discussionsStats":{"closed":0,"open":3,"total":3}}"><header class="from-gray-50-to-white border-b border-gray-100 bg-gradient-to-t via-white dark:via-gray-950 pt-6 sm:pt-9"><div class="container relative "><h1 class="flex flex-wrap items-center leading-tight mb-3 text-lg max-sm:gap-y-1.5 md:text-xl"><a href="/datasets" class="group flex items-center"><svg class="sm:mr-1.5 -mr-1 text-gray-400" style="" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 25 25"><ellipse cx="12.5" cy="5" fill="currentColor" fill-opacity="0.25" rx="7.5" ry="2"></ellipse><path d="M12.5 15C16.6421 15 20 14.1046 20 13V20C20 21.1046 16.6421 22 12.5 22C8.35786 22 5 21.1046 5 20V13C5 14.1046 8.35786 15 12.5 15Z" fill="currentColor" opacity="0.5"></path><path d="M12.5 7C16.6421 7 20 6.10457 20 5V11.5C20 12.6046 16.6421 13.5 12.5 13.5C8.35786 13.5 5 12.6046 5 11.5V5C5 6.10457 8.35786 7 12.5 7Z" fill="currentColor" opacity="0.5"></path><path d="M5.23628 12C5.08204 12.1598 5 12.8273 5 13C5 14.1046 8.35786 15 12.5 15C16.6421 15 20 14.1046 20 13C20 12.8273 19.918 12.1598 19.7637 12C18.9311 12.8626 15.9947 13.5 12.5 13.5C9.0053 13.5 6.06886 12.8626 5.23628 12Z" fill="currentColor"></path></svg> <span class="mr-2.5 font-semibold text-gray-400 group-hover:text-gray-500 max-sm:hidden">Datasets:</span></a> <hr class="mx-1.5 h-2 translate-y-px rounded-sm border-r dark:border-gray-600 sm:hidden"> <div class="group flex flex-none items-center"><div class="relative mr-1 flex items-center"> <span class="inline-block "><span class="contents"><a href="/AI-MO" class="text-gray-400 hover:text-blue-600"><img alt="" class="w-3.5 h-3.5 rounded flex-none" src="https://cdn-avatars.huggingface.co/v1/production/uploads/661d3f3e85f70e208d6f20db/kaXbnZDekN1gPzmRG_aFV.png" crossorigin="anonymous"></a></span> </span></div> <span class="inline-block "><span class="contents"><a href="/AI-MO" class="text-gray-400 hover:text-blue-600">AI-MO</a></span> </span> <div class="mx-0.5 text-gray-300">/</div></div> <div class="max-w-full "><a class="break-words font-mono font-semibold hover:text-blue-600 " href="/datasets/AI-MO/NuminaMath-1.5">NuminaMath-1.5</a> <button class="relative text-sm mr-4 inline-flex cursor-pointer items-center text-sm focus:outline-none mx-0.5 text-gray-600 " title="Copy dataset name to clipboard" type="button"><svg class="" xmlns="http://www.w3.org/2000/svg" aria-hidden="true" fill="currentColor" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32"><path d="M28,10V28H10V10H28m0-2H10a2,2,0,0,0-2,2V28a2,2,0,0,0,2,2H28a2,2,0,0,0,2-2V10a2,2,0,0,0-2-2Z" transform="translate(0)"></path><path d="M4,18H2V4A2,2,0,0,1,4,2H18V4H4Z" transform="translate(0)"></path><rect fill="none" width="32" height="32"></rect></svg> </button></div> <div class="inline-flex items-center overflow-hidden whitespace-nowrap rounded-md border bg-white text-sm leading-none text-gray-500 mr-2"><button class="relative flex items-center overflow-hidden from-red-50 to-transparent dark:from-red-900 px-1.5 py-1 hover:bg-gradient-to-t focus:outline-none" title="Like"><svg class="left-1.5 absolute" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32" fill="currentColor"><path d="M22.45,6a5.47,5.47,0,0,1,3.91,1.64,5.7,5.7,0,0,1,0,8L16,26.13,5.64,15.64a5.7,5.7,0,0,1,0-8,5.48,5.48,0,0,1,7.82,0L16,10.24l2.53-2.58A5.44,5.44,0,0,1,22.45,6m0-2a7.47,7.47,0,0,0-5.34,2.24L16,7.36,14.89,6.24a7.49,7.49,0,0,0-10.68,0,7.72,7.72,0,0,0,0,10.82L16,29,27.79,17.06a7.72,7.72,0,0,0,0-10.82A7.49,7.49,0,0,0,22.45,4Z"></path></svg> <span class="ml-4 pl-0.5 ">like</span></button> <button class="flex items-center border-l px-1.5 py-1 text-gray-400 hover:bg-gray-50 focus:bg-gray-100 focus:outline-none dark:hover:bg-gray-900 dark:focus:bg-gray-800" title="See users who liked this repository">106</button></div> <div class="relative flex items-center gap-1.5 "><div class="mr-2 inline-flex h-6 items-center overflow-hidden whitespace-nowrap rounded-md border text-sm text-gray-500"><button class="relative flex h-full max-w-56 items-center gap-1.5 overflow-hidden px-1.5 hover:bg-gray-50 focus:bg-gray-100 focus:outline-none dark:hover:bg-gray-900 dark:focus:bg-gray-800" type="button" ><div class="flex h-full flex-1 items-center justify-center ">Follow</div> <img alt="" class="size-3 flex-none rounded-sm" src="https://cdn-avatars.huggingface.co/v1/production/uploads/661d3f3e85f70e208d6f20db/kaXbnZDekN1gPzmRG_aFV.png"> <span class="truncate">Project-Numina</span></button> <button class="flex h-full items-center border-l pl-1.5 pr-1.5 text-gray-400 hover:bg-gray-50 focus:bg-gray-100 focus:outline-none dark:hover:bg-gray-900 dark:focus:bg-gray-800" title="Show Project-Numina's followers" type="button">248</button></div> </div> </h1> <div class="mb-3 flex flex-wrap md:mb-4"><div class="mr-1 flex flex-wrap items-center"><span class="mb-1 mr-1 p-1 text-sm leading-tight text-gray-400 md:mb-1.5">Tasks: </span> <a class="mb-1 mr-1 md:mb-1.5 md:mr-1.5 rounded-lg" href="/datasets?task_categories=task_categories%3Atext-generation"><div class="tag tag-white "><div class="tag-ico -ml-2 tag-ico-indigo"><svg class="" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" fill="currentColor" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 18 18"><path d="M16.2607 8.08202L14.468 6.28928C14.3063 6.12804 14.0873 6.03749 13.859 6.03749C13.6307 6.03749 13.4117 6.12804 13.25 6.28928L5.6375 13.904V16.9125H8.64607L16.2607 9.30002C16.422 9.13836 16.5125 8.91935 16.5125 8.69102C16.5125 8.4627 16.422 8.24369 16.2607 8.08202V8.08202ZM8.1953 15.825H6.725V14.3547L11.858 9.22118L13.3288 10.6915L8.1953 15.825ZM14.0982 9.92262L12.6279 8.45232L13.8606 7.21964L15.3309 8.68994L14.0982 9.92262Z"></path><path d="M6.18125 9.84373H7.26875V6.03748H8.9V4.94998H4.55V6.03748H6.18125V9.84373Z"></path><path d="M4.55 11.475H2.375V2.775H11.075V4.95H12.1625V2.775C12.1625 2.48658 12.0479 2.20997 11.844 2.00602C11.64 1.80208 11.3634 1.6875 11.075 1.6875H2.375C2.08658 1.6875 1.80997 1.80208 1.60602 2.00602C1.40207 2.20997 1.2875 2.48658 1.2875 2.775V11.475C1.2875 11.7634 1.40207 12.04 1.60602 12.244C1.80997 12.4479 2.08658 12.5625 2.375 12.5625H4.55V11.475Z"></path></svg></div> <span>Text Generation</span> </div></a> </div><div class="mr-1 flex flex-wrap items-center"><span class="mb-1 mr-1 p-1 text-sm leading-tight text-gray-400 md:mb-1.5">Modalities: </span> <a class="mb-1 mr-1 md:mb-1.5 md:mr-1.5 rounded-lg" href="/datasets?modality=modality%3Atext"><div class="tag tag-white "> <svg class="text-red-700 dark:text-red-600" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32"><path fill-rule="evenodd" clip-rule="evenodd" d="M4.619 4.619C2.667 6.573 2.667 9.715 2.667 16s0 9.428 1.952 11.38C6.573 29.333 9.715 29.333 16 29.333s9.428 0 11.38-1.953c1.953-1.95 1.953-5.095 1.953-11.38s0-9.428-1.953-11.381C25.43 2.667 22.285 2.667 16 2.667s-9.428 0-11.381 1.952m8.65 3.714c-.573 0-1.109 0-1.546.066-.495.073-1.003.248-1.41.7-.392.436-.53.956-.59 1.452-.056.464-.056 1.04-.056 1.689V13a1 1 0 1 0 2 0v-.704c0-.724.001-1.176.041-1.505q.015-.15.061-.294a.2.2 0 0 1 .031-.061q0-.003.016-.01a.8.8 0 0 1 .203-.05c.272-.04.654-.043 1.314-.043H15v11.334h-2.333a1 1 0 1 0 0 2H20a1 1 0 0 0 0-2h-3V10.333h1.667c.66 0 1.042.003 1.314.043.123.019.18.04.203.05l.015.009a.2.2 0 0 1 .032.061c.018.05.042.14.061.295.04.329.041.781.041 1.506V13a1 1 0 1 0 2 0v-.76c0-.65 0-1.225-.056-1.69-.06-.495-.198-1.015-.59-1.453-.407-.45-.915-.625-1.41-.698-.437-.067-.973-.067-1.546-.066z" fill="currentColor"></path></svg> <span>Text</span> </div></a> </div><div class="mr-1 flex flex-wrap items-center"><span class="mb-1 mr-1 p-1 text-sm leading-tight text-gray-400 md:mb-1.5">Formats: </span> <a class="mb-1 mr-1 md:mb-1.5 md:mr-1.5 rounded-lg" href="/datasets?format=format%3Aparquet"><div class="tag tag-white "> <svg class="" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 34 34"><path fill-rule="evenodd" clip-rule="evenodd" d="m17.97 18.44-3.98-2.3-7.1 3.78 3.98 2.3 7.1-3.78Zm15.1-1.4-3.99-2.3-16.22 8.63 3.98 2.3 16.22-8.63Zm-5.98-3.45-3.97-2.3-7.1 3.78 3.98 2.3 7.1-3.78Zm-9.94-5.74 3.98 2.3-11.16 5.93L6 13.78l11.16-5.93Zm-13.19 7 3.98 2.3-3.04 1.62-3.98-2.3 3.04-1.61Z" fill="currentColor"></path></svg> <span>parquet</span> </div></a> </div><div class="mr-1 flex flex-wrap items-center"><span class="mb-1 mr-1 p-1 text-sm leading-tight text-gray-400 md:mb-1.5">Languages: </span> <a class="mb-1 mr-1 md:mb-1.5 md:mr-1.5 rounded-lg" href="/datasets?language=language%3Aen"><div class="tag tag-white "> <svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" role="img" class="text-green-600/80" preserveAspectRatio="xMidYMid meet" width="1em" height="1em" viewBox="0 0 10 10"><path fill-rule="evenodd" clip-rule="evenodd" d="M0.625 5C0.625 6.16032 1.08594 7.27312 1.90641 8.09359C2.72688 8.91406 3.83968 9.375 5 9.375C6.16032 9.375 7.27312 8.91406 8.09359 8.09359C8.91406 7.27312 9.375 6.16032 9.375 5C9.375 3.83968 8.91406 2.72688 8.09359 1.90641C7.27312 1.08594 6.16032 0.625 5 0.625C3.83968 0.625 2.72688 1.08594 1.90641 1.90641C1.08594 2.72688 0.625 3.83968 0.625 5ZM7.64365 7.48027C7.61734 7.50832 7.59054 7.53598 7.56326 7.56326C7.13828 7.98824 6.61864 8.2968 6.0539 8.46842C6.29802 8.11949 6.49498 7.64804 6.63475 7.09483C7.00845 7.18834 7.35014 7.3187 7.64365 7.48027ZM8.10076 6.87776C8.37677 6.42196 8.55005 5.90894 8.60556 5.37499H6.86808C6.85542 5.71597 6.82551 6.04557 6.77971 6.35841C7.25309 6.47355 7.68808 6.6414 8.062 6.85549C8.07497 6.86283 8.08789 6.87025 8.10076 6.87776ZM6.03795 6.22536C6.07708 5.95737 6.1044 5.67232 6.11705 5.37499H3.88295C3.89666 5.69742 3.92764 6.00542 3.9722 6.29287C4.37075 6.21726 4.79213 6.17749 5.224 6.17749C5.50054 6.17749 5.77294 6.19376 6.03795 6.22536ZM4.1261 7.02673C4.34894 7.84835 4.68681 8.375 5 8.375C5.32122 8.375 5.66839 7.82101 5.8908 6.963C5.67389 6.93928 5.45082 6.92699 5.224 6.92699C4.84316 6.92699 4.47332 6.96176 4.1261 7.02673ZM3.39783 7.21853C3.53498 7.71842 3.72038 8.14579 3.9461 8.46842C3.42141 8.30898 2.93566 8.03132 2.52857 7.65192C2.77253 7.48017 3.06711 7.33382 3.39783 7.21853ZM3.23916 6.48077C3.18263 6.13193 3.14625 5.76074 3.13192 5.37499H1.39444C1.4585 5.99112 1.67936 6.57938 2.03393 7.08403C2.3706 6.83531 2.78055 6.63162 3.23916 6.48077ZM1.39444 4.62499H3.13192C3.14615 4.24204 3.18211 3.87344 3.23794 3.52681C2.77814 3.37545 2.36731 3.17096 2.03024 2.92123C1.67783 3.42469 1.45828 4.011 1.39444 4.62499ZM2.5237 2.35262C2.76812 2.52552 3.06373 2.67281 3.39584 2.78875C3.53318 2.28573 3.71928 1.85578 3.9461 1.53158C3.41932 1.69166 2.93178 1.97089 2.5237 2.35262ZM3.97101 3.71489C3.92709 4.00012 3.89654 4.30547 3.88295 4.62499H6.11705C6.10453 4.33057 6.07761 4.04818 6.03909 3.78248C5.77372 3.81417 5.50093 3.83049 5.224 3.83049C4.79169 3.83049 4.3699 3.79065 3.97101 3.71489ZM5.8928 3.04476C5.67527 3.06863 5.45151 3.08099 5.224 3.08099C4.84241 3.08099 4.47186 3.04609 4.12405 2.98086C4.34686 2.1549 4.68584 1.625 5 1.625C5.32218 1.625 5.67048 2.18233 5.8928 3.04476ZM6.78083 3.6493C6.826 3.95984 6.85552 4.28682 6.86808 4.62499H8.60556C8.55029 4.09337 8.37827 3.58251 8.10436 3.1282C8.0903 3.1364 8.07618 3.14449 8.062 3.15249C7.68838 3.36641 7.25378 3.53417 6.78083 3.6493ZM7.64858 2.52499C7.35446 2.68754 7.0117 2.81868 6.63664 2.91268C6.49676 2.35623 6.29913 1.88209 6.0539 1.53158C6.61864 1.7032 7.13828 2.01176 7.56326 2.43674C7.59224 2.46572 7.62068 2.49514 7.64858 2.52499Z" fill="currentColor"></path></svg> <span>English</span> </div></a> </div><div class="mr-1 flex flex-wrap items-center"><span class="mb-1 mr-1 p-1 text-sm leading-tight text-gray-400 md:mb-1.5">Size: </span> <a class="mb-1 mr-1 md:mb-1.5 md:mr-1.5 rounded-lg" href="/datasets?size_categories=size_categories%3A100K%3Cn%3C1M"><div class="tag tag-white "> <span>100K - 1M</span> </div></a> </div><div class="mr-1 flex flex-wrap items-center"><span class="mb-1 mr-1 p-1 text-sm leading-tight text-gray-400 md:mb-1.5">Tags: </span> <a class="mb-1 mr-1 md:mb-1.5 md:mr-1.5 rounded-lg" href="/datasets?other=math"><div class="tag tag-white "> <span>math</span> </div></a><a class="mb-1 mr-1 md:mb-1.5 md:mr-1.5 rounded-lg" href="/datasets?other=post-training"><div class="tag tag-white "> <span>post-training</span> </div></a> </div><div class="mr-1 flex flex-wrap items-center"><span class="mb-1 mr-1 p-1 text-sm leading-tight text-gray-400 md:mb-1.5">Libraries: </span> <a class="mb-1 mr-1 md:mb-1.5 md:mr-1.5 rounded-lg" href="/datasets?library=library%3Adatasets"><div class="tag tag-white "><svg class="text-black inline-block text-sm" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" preserveAspectRatio="xMidYMid meet" width="1em" height="1em" viewBox="0 0 95 88"><path fill="#fff" d="M94.25 70.08a8.28 8.28 0 0 1-.43 6.46 10.57 10.57 0 0 1-3 3.6 25.18 25.18 0 0 1-5.7 3.2 65.74 65.74 0 0 1-7.56 2.65 46.67 46.67 0 0 1-11.42 1.68c-5.42.05-10.09-1.23-13.4-4.5a40.4 40.4 0 0 1-10.14.03c-3.34 3.25-7.99 4.52-13.39 4.47a46.82 46.82 0 0 1-11.43-1.68 66.37 66.37 0 0 1-7.55-2.65c-2.28-.98-4.17-2-5.68-3.2a10.5 10.5 0 0 1-3.02-3.6c-.99-2-1.18-4.3-.42-6.46a8.54 8.54 0 0 1-.33-5.63c.25-.95.66-1.83 1.18-2.61a8.67 8.67 0 0 1 2.1-8.47 8.23 8.23 0 0 1 2.82-2.07 41.75 41.75 0 1 1 81.3-.12 8.27 8.27 0 0 1 3.11 2.19 8.7 8.7 0 0 1 2.1 8.47c.52.78.93 1.66 1.18 2.61a8.61 8.61 0 0 1-.32 5.63Z"></path><path fill="#FFD21E" d="M47.21 76.5a34.75 34.75 0 1 0 0-69.5 34.75 34.75 0 0 0 0 69.5Z"></path><path fill="#FF9D0B" d="M81.96 41.75a34.75 34.75 0 1 0-69.5 0 34.75 34.75 0 0 0 69.5 0Zm-73.5 0a38.75 38.75 0 1 1 77.5 0 38.75 38.75 0 0 1-77.5 0Z"></path><path fill="#3A3B45" d="M58.5 32.3c1.28.44 1.78 3.06 3.07 2.38a5 5 0 1 0-6.76-2.07c.61 1.15 2.55-.72 3.7-.32ZM34.95 32.3c-1.28.44-1.79 3.06-3.07 2.38a5 5 0 1 1 6.76-2.07c-.61 1.15-2.56-.72-3.7-.32Z"></path><path fill="#FF323D" d="M46.96 56.29c9.83 0 13-8.76 13-13.26 0-2.34-1.57-1.6-4.09-.36-2.33 1.15-5.46 2.74-8.9 2.74-7.19 0-13-6.88-13-2.38s3.16 13.26 13 13.26Z"></path><path fill="#3A3B45" fill-rule="evenodd" d="M39.43 54a8.7 8.7 0 0 1 5.3-4.49c.4-.12.81.57 1.24 1.28.4.68.82 1.37 1.24 1.37.45 0 .9-.68 1.33-1.35.45-.7.89-1.38 1.32-1.25a8.61 8.61 0 0 1 5 4.17c3.73-2.94 5.1-7.74 5.1-10.7 0-2.34-1.57-1.6-4.09-.36l-.14.07c-2.31 1.15-5.39 2.67-8.77 2.67s-6.45-1.52-8.77-2.67c-2.6-1.29-4.23-2.1-4.23.29 0 3.05 1.46 8.06 5.47 10.97Z" clip-rule="evenodd"></path><path fill="#FF9D0B" d="M70.71 37a3.25 3.25 0 1 0 0-6.5 3.25 3.25 0 0 0 0 6.5ZM24.21 37a3.25 3.25 0 1 0 0-6.5 3.25 3.25 0 0 0 0 6.5ZM17.52 48c-1.62 0-3.06.66-4.07 1.87a5.97 5.97 0 0 0-1.33 3.76 7.1 7.1 0 0 0-1.94-.3c-1.55 0-2.95.59-3.94 1.66a5.8 5.8 0 0 0-.8 7 5.3 5.3 0 0 0-1.79 2.82c-.24.9-.48 2.8.8 4.74a5.22 5.22 0 0 0-.37 5.02c1.02 2.32 3.57 4.14 8.52 6.1 3.07 1.22 5.89 2 5.91 2.01a44.33 44.33 0 0 0 10.93 1.6c5.86 0 10.05-1.8 12.46-5.34 3.88-5.69 3.33-10.9-1.7-15.92-2.77-2.78-4.62-6.87-5-7.77-.78-2.66-2.84-5.62-6.25-5.62a5.7 5.7 0 0 0-4.6 2.46c-1-1.26-1.98-2.25-2.86-2.82A7.4 7.4 0 0 0 17.52 48Zm0 4c.51 0 1.14.22 1.82.65 2.14 1.36 6.25 8.43 7.76 11.18.5.92 1.37 1.31 2.14 1.31 1.55 0 2.75-1.53.15-3.48-3.92-2.93-2.55-7.72-.68-8.01.08-.02.17-.02.24-.02 1.7 0 2.45 2.93 2.45 2.93s2.2 5.52 5.98 9.3c3.77 3.77 3.97 6.8 1.22 10.83-1.88 2.75-5.47 3.58-9.16 3.58-3.81 0-7.73-.9-9.92-1.46-.11-.03-13.45-3.8-11.76-7 .28-.54.75-.76 1.34-.76 2.38 0 6.7 3.54 8.57 3.54.41 0 .7-.17.83-.6.79-2.85-12.06-4.05-10.98-8.17.2-.73.71-1.02 1.44-1.02 3.14 0 10.2 5.53 11.68 5.53.11 0 .2-.03.24-.1.74-1.2.33-2.04-4.9-5.2-5.21-3.16-8.88-5.06-6.8-7.33.24-.26.58-.38 1-.38 3.17 0 10.66 6.82 10.66 6.82s2.02 2.1 3.25 2.1c.28 0 .52-.1.68-.38.86-1.46-8.06-8.22-8.56-11.01-.34-1.9.24-2.85 1.31-2.85Z"></path><path fill="#FFD21E" d="M38.6 76.69c2.75-4.04 2.55-7.07-1.22-10.84-3.78-3.77-5.98-9.3-5.98-9.3s-.82-3.2-2.69-2.9c-1.87.3-3.24 5.08.68 8.01 3.91 2.93-.78 4.92-2.29 2.17-1.5-2.75-5.62-9.82-7.76-11.18-2.13-1.35-3.63-.6-3.13 2.2.5 2.79 9.43 9.55 8.56 11-.87 1.47-3.93-1.71-3.93-1.71s-9.57-8.71-11.66-6.44c-2.08 2.27 1.59 4.17 6.8 7.33 5.23 3.16 5.64 4 4.9 5.2-.75 1.2-12.28-8.53-13.36-4.4-1.08 4.11 11.77 5.3 10.98 8.15-.8 2.85-9.06-5.38-10.74-2.18-1.7 3.21 11.65 6.98 11.76 7.01 4.3 1.12 15.25 3.49 19.08-2.12Z"></path><path fill="#FF9D0B" d="M77.4 48c1.62 0 3.07.66 4.07 1.87a5.97 5.97 0 0 1 1.33 3.76 7.1 7.1 0 0 1 1.95-.3c1.55 0 2.95.59 3.94 1.66a5.8 5.8 0 0 1 .8 7 5.3 5.3 0 0 1 1.78 2.82c.24.9.48 2.8-.8 4.74a5.22 5.22 0 0 1 .37 5.02c-1.02 2.32-3.57 4.14-8.51 6.1-3.08 1.22-5.9 2-5.92 2.01a44.33 44.33 0 0 1-10.93 1.6c-5.86 0-10.05-1.8-12.46-5.34-3.88-5.69-3.33-10.9 1.7-15.92 2.78-2.78 4.63-6.87 5.01-7.77.78-2.66 2.83-5.62 6.24-5.62a5.7 5.7 0 0 1 4.6 2.46c1-1.26 1.98-2.25 2.87-2.82A7.4 7.4 0 0 1 77.4 48Zm0 4c-.51 0-1.13.22-1.82.65-2.13 1.36-6.25 8.43-7.76 11.18a2.43 2.43 0 0 1-2.14 1.31c-1.54 0-2.75-1.53-.14-3.48 3.91-2.93 2.54-7.72.67-8.01a1.54 1.54 0 0 0-.24-.02c-1.7 0-2.45 2.93-2.45 2.93s-2.2 5.52-5.97 9.3c-3.78 3.77-3.98 6.8-1.22 10.83 1.87 2.75 5.47 3.58 9.15 3.58 3.82 0 7.73-.9 9.93-1.46.1-.03 13.45-3.8 11.76-7-.29-.54-.75-.76-1.34-.76-2.38 0-6.71 3.54-8.57 3.54-.42 0-.71-.17-.83-.6-.8-2.85 12.05-4.05 10.97-8.17-.19-.73-.7-1.02-1.44-1.02-3.14 0-10.2 5.53-11.68 5.53-.1 0-.19-.03-.23-.1-.74-1.2-.34-2.04 4.88-5.2 5.23-3.16 8.9-5.06 6.8-7.33-.23-.26-.57-.38-.98-.38-3.18 0-10.67 6.82-10.67 6.82s-2.02 2.1-3.24 2.1a.74.74 0 0 1-.68-.38c-.87-1.46 8.05-8.22 8.55-11.01.34-1.9-.24-2.85-1.31-2.85Z"></path><path fill="#FFD21E" d="M56.33 76.69c-2.75-4.04-2.56-7.07 1.22-10.84 3.77-3.77 5.97-9.3 5.97-9.3s.82-3.2 2.7-2.9c1.86.3 3.23 5.08-.68 8.01-3.92 2.93.78 4.92 2.28 2.17 1.51-2.75 5.63-9.82 7.76-11.18 2.13-1.35 3.64-.6 3.13 2.2-.5 2.79-9.42 9.55-8.55 11 .86 1.47 3.92-1.71 3.92-1.71s9.58-8.71 11.66-6.44c2.08 2.27-1.58 4.17-6.8 7.33-5.23 3.16-5.63 4-4.9 5.2.75 1.2 12.28-8.53 13.36-4.4 1.08 4.11-11.76 5.3-10.97 8.15.8 2.85 9.05-5.38 10.74-2.18 1.69 3.21-11.65 6.98-11.76 7.01-4.31 1.12-15.26 3.49-19.08-2.12Z"></path></svg> <span>Datasets</span> </div></a><a class="mb-1 mr-1 md:mb-1.5 md:mr-1.5 rounded-lg" href="/datasets?library=library%3Adask"><div class="tag tag-white "><svg class="text-black inline-block text-sm" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" fill="currentColor" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 12 12"><path d="m3.368 3.694 2.965-1.71A.095.095 0 0 0 6.38 1.9V.875a.49.49 0 0 0-.183-.394.468.468 0 0 0-.523-.034L1.526 2.84a.471.471 0 0 0-.235.408l-.002 5.405c0 .151.062.302.183.394.157.118.358.13.524.035l.878-.507a.095.095 0 0 0 .048-.082V4.465a.89.89 0 0 1 .446-.771Z" fill="#FFC11E"></path><path d="M10.475 2.919a.47.47 0 0 0-.47 0L5.856 5.312a.473.473 0 0 0-.236.408l-.002 5.425c0 .17.088.323.236.408a.466.466 0 0 0 .471 0l4.147-2.393a.473.473 0 0 0 .236-.408l.002-5.425a.467.467 0 0 0-.236-.408Z" fill="#EF1161"></path><path d="m5.647 4.949 2.737-1.58a.095.095 0 0 0 .047-.082V2.093a.49.49 0 0 0-.183-.394.468.468 0 0 0-.523-.035l-1.135.655-3.013 1.738a.471.471 0 0 0-.236.408v4.083L3.34 9.87c0 .152.062.302.183.394.157.118.358.13.524.035l1.106-.639a.094.094 0 0 0 .047-.082l.001-3.859a.89.89 0 0 1 .446-.77Z" fill="#FC6E6B"></path></svg> <span>Dask</span> </div></a><div class="relative inline-block "> <button class="group mr-1 mb-1 md:mr-1.5 md:mb-1.5 rounded-lg rounded-br-none " type="button"> <div class="tag tag-white relative rounded-br-none pr-2.5"><svg class="text-black inline-block text-sm" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" fill="none" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32"><path d="M22.2812 12.2656L25.9532 15.7187C26.8932 16.6587 28.0913 17.3931 29.0313 16.4531C29.8594 15.7812 29.9332 14.1 29.9532 13.5C29.9532 11.5625 28.9219 8.375 27.25 6.71875C25.5604 5.04493 23.3782 3.91692 22.7032 3.78125L22.2812 12.2656Z" fill="#F5AB6A"></path><path d="M22.2812 12.2656L25.9532 15.7187C26.8932 16.6587 28.0913 17.3931 29.0313 16.4531C29.8594 15.7812 29.9332 14.1 29.9532 13.5C29.9532 11.5625 28.9219 8.375 27.25 6.71875C25.5604 5.04493 23.3782 3.91692 22.7032 3.78125L22.2812 12.2656Z" fill="url(#paint0_radial_18_31665)"></path><g filter="url(#filter0_f_18_31665)"><path d="M22.2849 12.1817L23.4375 13.2656L24.4375 4.70312C23.5121 4.1242 23.0198 3.96369 22.6563 3.89062L22.2849 12.1817Z" fill="url(#paint1_linear_18_31665)"></path></g><path d="M22.7969 3.05741L21.8437 2.65269C19.6421 1.96765 17.2344 1.81208 14.6719 2.23236C12.1094 2.65264 11.5156 3.2442 11.5156 3.2442C10.896 3.3674 10.8671 3.88898 11.1718 4.45363C13.0797 6.72576 15.176 13.4043 18.0469 14.2506C18.89 14.4662 21.3791 14.4776 22.2019 14.1593L22.3238 14.108C22.6692 13.9745 23.1672 13.2814 23.1875 12.9118L23.4219 4.03043C23.4523 3.59924 23.1484 3.25204 22.7969 3.05741Z" fill="url(#paint2_radial_18_31665)"></path><path d="M22.7969 3.05741L21.8437 2.65269C19.6421 1.96765 17.2344 1.81208 14.6719 2.23236C12.1094 2.65264 11.5156 3.2442 11.5156 3.2442C10.896 3.3674 10.8671 3.88898 11.1718 4.45363C13.0797 6.72576 15.176 13.4043 18.0469 14.2506C18.89 14.4662 21.3791 14.4776 22.2019 14.1593L22.3238 14.108C22.6692 13.9745 23.1672 13.2814 23.1875 12.9118L23.4219 4.03043C23.4523 3.59924 23.1484 3.25204 22.7969 3.05741Z" fill="url(#paint3_radial_18_31665)"></path><path d="M22.7969 3.05741L21.8437 2.65269C19.6421 1.96765 17.2344 1.81208 14.6719 2.23236C12.1094 2.65264 11.5156 3.2442 11.5156 3.2442C10.896 3.3674 10.8671 3.88898 11.1718 4.45363C13.0797 6.72576 15.176 13.4043 18.0469 14.2506C18.89 14.4662 21.3791 14.4776 22.2019 14.1593L22.3238 14.108C22.6692 13.9745 23.1672 13.2814 23.1875 12.9118L23.4219 4.03043C23.4523 3.59924 23.1484 3.25204 22.7969 3.05741Z" fill="url(#paint4_radial_18_31665)"></path><path d="M22.7969 3.05741L21.8437 2.65269C19.6421 1.96765 17.2344 1.81208 14.6719 2.23236C12.1094 2.65264 11.5156 3.2442 11.5156 3.2442C10.896 3.3674 10.8671 3.88898 11.1718 4.45363C13.0797 6.72576 15.176 13.4043 18.0469 14.2506C18.89 14.4662 21.3791 14.4776 22.2019 14.1593L22.3238 14.108C22.6692 13.9745 23.1672 13.2814 23.1875 12.9118L23.4219 4.03043C23.4523 3.59924 23.1484 3.25204 22.7969 3.05741Z" fill="url(#paint5_radial_18_31665)"></path><path d="M22.7969 3.05741L21.8437 2.65269C19.6421 1.96765 17.2344 1.81208 14.6719 2.23236C12.1094 2.65264 11.5156 3.2442 11.5156 3.2442C10.896 3.3674 10.8671 3.88898 11.1718 4.45363C13.0797 6.72576 15.176 13.4043 18.0469 14.2506C18.89 14.4662 21.3791 14.4776 22.2019 14.1593L22.3238 14.108C22.6692 13.9745 23.1672 13.2814 23.1875 12.9118L23.4219 4.03043C23.4523 3.59924 23.1484 3.25204 22.7969 3.05741Z" fill="url(#paint6_linear_18_31665)"></path><g filter="url(#filter1_f_18_31665)"><path d="M13.1016 2.72656C11.862 3.06924 11.5298 3.40016 11.5298 3.40016C10.9102 3.52335 10.936 4.11525 11.2408 4.6799C13.1487 6.95202 15.1361 13.2496 18.007 14.0958C18.2707 14.1633 18.6953 14.2107 19.1797 14.2344L13.1016 2.72656Z" fill="url(#paint7_linear_18_31665)"></path></g><path d="M12.2187 22.7187L15.7656 26.2031C16.7332 27.1171 17.3334 28.2487 16.4219 29.2188C15.7749 30.0687 14.2241 29.9933 13.625 30.0313C11.6883 30.0891 9.09014 29.5622 6.84373 27.5313C5.07737 25.9343 4.09321 23.688 3.93751 23.0156L12.2187 22.7187Z" fill="url(#paint8_radial_18_31665)"></path><path d="M12.2187 22.7187L15.7656 26.2031C16.7332 27.1171 17.3334 28.2487 16.4219 29.2188C15.7749 30.0687 14.2241 29.9933 13.625 30.0313C11.6883 30.0891 9.09014 29.5622 6.84373 27.5313C5.07737 25.9343 4.09321 23.688 3.93751 23.0156L12.2187 22.7187Z" fill="url(#paint9_radial_18_31665)"></path><g filter="url(#filter2_f_18_31665)"><path d="M12.0523 22.7916L13.2187 23.9375L4.81018 24.5721C4.4328 23.8671 4.20835 23.2768 4.14062 22.9844L12.0523 22.7916Z" fill="url(#paint10_linear_18_31665)"></path><path d="M12.0523 22.7916L13.2187 23.9375L4.81018 24.5721C4.4328 23.8671 4.20835 23.2768 4.14062 22.9844L12.0523 22.7916Z" fill="url(#paint11_radial_18_31665)"></path></g><path d="M2.99219 22.6484C2.07068 20.538 1.78913 17.4452 2.21096 15.0703C2.63279 12.6953 3.20759 11.951 3.20759 11.951C3.31231 11.3264 3.83281 11.2818 4.40626 11.5703C6.73409 13.4144 13.3119 15.2264 14.2432 18.0781C14.5947 19.3034 14.6279 21.3125 14.1641 22.5156C14.0409 22.8657 13.5 23.3516 13.0625 23.4141C12.625 23.4765 9.47656 23.3516 8.61719 23.3516C7.75781 23.3516 4.64844 23.6719 4.14062 23.6172C3.63281 23.5625 3.23437 23.2031 2.99219 22.6484Z" fill="#EC9F6A"></path><path d="M2.99219 22.6484C2.07068 20.538 1.78913 17.4452 2.21096 15.0703C2.63279 12.6953 3.20759 11.951 3.20759 11.951C3.31231 11.3264 3.83281 11.2818 4.40626 11.5703C6.73409 13.4144 13.3119 15.2264 14.2432 18.0781C14.5947 19.3034 14.6279 21.3125 14.1641 22.5156C14.0409 22.8657 13.5 23.3516 13.0625 23.4141C12.625 23.4765 9.47656 23.3516 8.61719 23.3516C7.75781 23.3516 4.64844 23.6719 4.14062 23.6172C3.63281 23.5625 3.23437 23.2031 2.99219 22.6484Z" fill="url(#paint12_radial_18_31665)"></path><path d="M2.99219 22.6484C2.07068 20.538 1.78913 17.4452 2.21096 15.0703C2.63279 12.6953 3.20759 11.951 3.20759 11.951C3.31231 11.3264 3.83281 11.2818 4.40626 11.5703C6.73409 13.4144 13.3119 15.2264 14.2432 18.0781C14.5947 19.3034 14.6279 21.3125 14.1641 22.5156C14.0409 22.8657 13.5 23.3516 13.0625 23.4141C12.625 23.4765 9.47656 23.3516 8.61719 23.3516C7.75781 23.3516 4.64844 23.6719 4.14062 23.6172C3.63281 23.5625 3.23437 23.2031 2.99219 22.6484Z" fill="url(#paint13_linear_18_31665)"></path><path d="M2.99219 22.6484C2.07068 20.538 1.78913 17.4452 2.21096 15.0703C2.63279 12.6953 3.20759 11.951 3.20759 11.951C3.31231 11.3264 3.83281 11.2818 4.40626 11.5703C6.73409 13.4144 13.3119 15.2264 14.2432 18.0781C14.5947 19.3034 14.6279 21.3125 14.1641 22.5156C14.0409 22.8657 13.5 23.3516 13.0625 23.4141C12.625 23.4765 9.47656 23.3516 8.61719 23.3516C7.75781 23.3516 4.64844 23.6719 4.14062 23.6172C3.63281 23.5625 3.23437 23.2031 2.99219 22.6484Z" fill="url(#paint14_radial_18_31665)"></path><path d="M2.99219 22.6484C2.07068 20.538 1.78913 17.4452 2.21096 15.0703C2.63279 12.6953 3.20759 11.951 3.20759 11.951C3.31231 11.3264 3.83281 11.2818 4.40626 11.5703C6.73409 13.4144 13.3119 15.2264 14.2432 18.0781C14.5947 19.3034 14.6279 21.3125 14.1641 22.5156C14.0409 22.8657 13.5 23.3516 13.0625 23.4141C12.625 23.4765 9.47656 23.3516 8.61719 23.3516C7.75781 23.3516 4.64844 23.6719 4.14062 23.6172C3.63281 23.5625 3.23437 23.2031 2.99219 22.6484Z" fill="url(#paint15_radial_18_31665)"></path><path d="M2.99219 22.6484C2.07068 20.538 1.78913 17.4452 2.21096 15.0703C2.63279 12.6953 3.20759 11.951 3.20759 11.951C3.31231 11.3264 3.83281 11.2818 4.40626 11.5703C6.73409 13.4144 13.3119 15.2264 14.2432 18.0781C14.5947 19.3034 14.6279 21.3125 14.1641 22.5156C14.0409 22.8657 13.5 23.3516 13.0625 23.4141C12.625 23.4765 9.47656 23.3516 8.61719 23.3516C7.75781 23.3516 4.64844 23.6719 4.14062 23.6172C3.63281 23.5625 3.23437 23.2031 2.99219 22.6484Z" fill="url(#paint16_radial_18_31665)"></path><g filter="url(#filter3_f_18_31665)"><path d="M2.70313 13.6719C3.04135 12.4711 3.36224 12.0555 3.36224 12.0555C3.46697 11.4309 3.98746 11.3864 4.56092 11.6749C6.88874 13.5189 13.0809 15.1104 14.0121 17.9622C14.1731 18.5231 14.2766 19.0394 14.3287 19.5128L2.70313 13.6719Z" fill="url(#paint17_linear_18_31665)"></path><path d="M2.70313 13.6719C3.04135 12.4711 3.36224 12.0555 3.36224 12.0555C3.46697 11.4309 3.98746 11.3864 4.56092 11.6749C6.88874 13.5189 13.0809 15.1104 14.0121 17.9622C14.1731 18.5231 14.2766 19.0394 14.3287 19.5128L2.70313 13.6719Z" fill="url(#paint18_linear_18_31665)"></path></g><path d="M9.83184 2.82184C6.62184 4.07184 4.07184 6.62184 2.82184 9.83184C2.48184 10.7118 2.82184 11.7018 3.62184 12.1918L14.0418 18.5418C14.6618 18.9218 15.4418 18.9218 16.0618 18.5418C17.0718 17.9218 17.9318 17.0718 18.5418 16.0618C18.9218 15.4418 18.9218 14.6618 18.5418 14.0418L12.1918 3.62184C11.7018 2.82184 10.7118 2.48184 9.83184 2.82184Z" fill="#D79453"></path><path d="M9.83184 2.82184C6.62184 4.07184 4.07184 6.62184 2.82184 9.83184C2.48184 10.7118 2.82184 11.7018 3.62184 12.1918L14.0418 18.5418C14.6618 18.9218 15.4418 18.9218 16.0618 18.5418C17.0718 17.9218 17.9318 17.0718 18.5418 16.0618C18.9218 15.4418 18.9218 14.6618 18.5418 14.0418L12.1918 3.62184C11.7018 2.82184 10.7118 2.48184 9.83184 2.82184Z" fill="url(#paint19_radial_18_31665)"></path><path d="M9.83184 2.82184C6.62184 4.07184 4.07184 6.62184 2.82184 9.83184C2.48184 10.7118 2.82184 11.7018 3.62184 12.1918L14.0418 18.5418C14.6618 18.9218 15.4418 18.9218 16.0618 18.5418C17.0718 17.9218 17.9318 17.0718 18.5418 16.0618C18.9218 15.4418 18.9218 14.6618 18.5418 14.0418L12.1918 3.62184C11.7018 2.82184 10.7118 2.48184 9.83184 2.82184Z" fill="url(#paint20_radial_18_31665)"></path><path d="M9.83184 2.82184C6.62184 4.07184 4.07184 6.62184 2.82184 9.83184C2.48184 10.7118 2.82184 11.7018 3.62184 12.1918L14.0418 18.5418C14.6618 18.9218 15.4418 18.9218 16.0618 18.5418C17.0718 17.9218 17.9318 17.0718 18.5418 16.0618C18.9218 15.4418 18.9218 14.6618 18.5418 14.0418L12.1918 3.62184C11.7018 2.82184 10.7118 2.48184 9.83184 2.82184Z" fill="url(#paint21_radial_18_31665)"></path><path d="M9.83184 2.82184C6.62184 4.07184 4.07184 6.62184 2.82184 9.83184C2.48184 10.7118 2.82184 11.7018 3.62184 12.1918L14.0418 18.5418C14.6618 18.9218 15.4418 18.9218 16.0618 18.5418C17.0718 17.9218 17.9318 17.0718 18.5418 16.0618C18.9218 15.4418 18.9218 14.6618 18.5418 14.0418L12.1918 3.62184C11.7018 2.82184 10.7118 2.48184 9.83184 2.82184Z" fill="url(#paint22_linear_18_31665)"></path><path d="M9.83184 2.82184C6.62184 4.07184 4.07184 6.62184 2.82184 9.83184C2.48184 10.7118 2.82184 11.7018 3.62184 12.1918L14.0418 18.5418C14.6618 18.9218 15.4418 18.9218 16.0618 18.5418C17.0718 17.9218 17.9318 17.0718 18.5418 16.0618C18.9218 15.4418 18.9218 14.6618 18.5418 14.0418L12.1918 3.62184C11.7018 2.82184 10.7118 2.48184 9.83184 2.82184Z" fill="url(#paint23_radial_18_31665)"></path><path d="M9.83184 2.82184C6.62184 4.07184 4.07184 6.62184 2.82184 9.83184C2.48184 10.7118 2.82184 11.7018 3.62184 12.1918L14.0418 18.5418C14.6618 18.9218 15.4418 18.9218 16.0618 18.5418C17.0718 17.9218 17.9318 17.0718 18.5418 16.0618C18.9218 15.4418 18.9218 14.6618 18.5418 14.0418L12.1918 3.62184C11.7018 2.82184 10.7118 2.48184 9.83184 2.82184Z" fill="url(#paint24_radial_18_31665)"></path><defs><filter id="filter0_f_18_31665" x="22.0349" y="3.64062" width="2.65265" height="9.875" filterUnits="userSpaceOnUse" color-interpolation-filters="sRGB"><feFlood flood-opacity="0" result="BackgroundImageFix"></feFlood><feBlend mode="normal" in="SourceGraphic" in2="BackgroundImageFix" result="shape"></feBlend><feGaussianBlur stdDeviation="0.125" result="effect1_foregroundBlur_18_31665"></feGaussianBlur></filter><filter id="filter1_f_18_31665" x="10.7815" y="2.47656" width="8.64819" height="12.0078" filterUnits="userSpaceOnUse" color-interpolation-filters="sRGB"><feFlood flood-opacity="0" result="BackgroundImageFix"></feFlood><feBlend mode="normal" in="SourceGraphic" in2="BackgroundImageFix" result="shape"></feBlend><feGaussianBlur stdDeviation="0.125" result="effect1_foregroundBlur_18_31665"></feGaussianBlur></filter><filter id="filter2_f_18_31665" x="3.89062" y="22.5416" width="9.57812" height="2.2804" filterUnits="userSpaceOnUse" color-interpolation-filters="sRGB"><feFlood flood-opacity="0" result="BackgroundImageFix"></feFlood><feBlend mode="normal" in="SourceGraphic" in2="BackgroundImageFix" result="shape"></feBlend><feGaussianBlur stdDeviation="0.125" result="effect1_foregroundBlur_18_31665"></feGaussianBlur></filter><filter id="filter3_f_18_31665" x="2.45312" y="11.2538" width="12.1255" height="8.50903" filterUnits="userSpaceOnUse" color-interpolation-filters="sRGB"><feFlood flood-opacity="0" result="BackgroundImageFix"></feFlood><feBlend mode="normal" in="SourceGraphic" in2="BackgroundImageFix" result="shape"></feBlend><feGaussianBlur stdDeviation="0.125" result="effect1_foregroundBlur_18_31665"></feGaussianBlur></filter><radialGradient id="paint0_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(22.8125 12.9375) rotate(42.7741) scale(12.5164 7.08839)"><stop offset="0.0937591" stop-color="#C05159"></stop><stop offset="0.553697" stop-color="#F6AC6A"></stop><stop offset="0.832916" stop-color="#FFD186"></stop><stop offset="0.916927" stop-color="#FFDC87"></stop></radialGradient><linearGradient id="paint1_linear_18_31665" x1="24.7344" y1="4.67187" x2="20.8594" y2="12.8906" gradientUnits="userSpaceOnUse"><stop stop-color="#EBD67C"></stop><stop offset="0.0655686" stop-color="#FFFFA6"></stop><stop offset="0.530552" stop-color="#F8C281"></stop><stop offset="0.937338" stop-color="#E99E6B"></stop></linearGradient><radialGradient id="paint2_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(22.9009 13.1847) rotate(-127.648) scale(14.3438 11.7966)"><stop stop-color="#FFBE66"></stop><stop offset="1" stop-color="#E2AE5B"></stop></radialGradient><radialGradient id="paint3_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(18 11.4375) rotate(53.9726) scale(11.9013 4.84018)"><stop stop-color="#D67C63"></stop><stop offset="1" stop-color="#D97D67" stop-opacity="0"></stop></radialGradient><radialGradient id="paint4_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(23 4.1875) rotate(45.7639) scale(3.31486 5.75622)"><stop stop-color="#FFE4A6"></stop><stop offset="0.711285" stop-color="#F8B76F"></stop><stop offset="1" stop-color="#F9B870" stop-opacity="0"></stop></radialGradient><radialGradient id="paint5_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(22.875 12.4375) rotate(88.9391) scale(3.37558 1.29066)"><stop stop-color="#FFBC67"></stop><stop offset="1" stop-color="#FFBC67" stop-opacity="0"></stop></radialGradient><linearGradient id="paint6_linear_18_31665" x1="20.375" y1="15.6875" x2="20.125" y2="12.7813" gradientUnits="userSpaceOnUse"><stop offset="0.461609" stop-color="#B45077"></stop><stop offset="0.855389" stop-color="#B75077" stop-opacity="0"></stop></linearGradient><linearGradient id="paint7_linear_18_31665" x1="12.9375" y1="2.57056" x2="18.5625" y2="14.3891" gradientUnits="userSpaceOnUse"><stop stop-color="#DDC173"></stop><stop offset="0.485173" stop-color="#D59F65"></stop><stop offset="1" stop-color="#E49966"></stop></linearGradient><radialGradient id="paint8_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(13.5625 23.5) rotate(109.113) scale(6.68078 10.2578)"><stop offset="0.165756" stop-color="#FFBF7E"></stop><stop offset="0.827674" stop-color="#DF8C6D"></stop><stop offset="1" stop-color="#B05A66"></stop></radialGradient><radialGradient id="paint9_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(15.1875 26) rotate(41.0652) scale(8.37243 2.03649)"><stop stop-color="#FFD483"></stop><stop offset="1" stop-color="#FFD688" stop-opacity="0"></stop></radialGradient><linearGradient id="paint10_linear_18_31665" x1="3.96063" y1="23.794" x2="13.3748" y2="23.5143" gradientUnits="userSpaceOnUse"><stop stop-color="#A8716F"></stop><stop offset="0.103615" stop-color="#B37173"></stop><stop offset="0.225484" stop-color="#DB9F84"></stop><stop offset="0.799889" stop-color="#F1BB8A"></stop><stop offset="1" stop-color="#FFD780"></stop></linearGradient><radialGradient id="paint11_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(11.4219 23.1719) rotate(-178.616) scale(3.23532 0.569081)"><stop offset="0.621498" stop-color="#AF5A3E"></stop><stop offset="1" stop-color="#B35445" stop-opacity="0"></stop></radialGradient><radialGradient id="paint12_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(13.625 19.125) rotate(-171.737) scale(15.2205 15.0767)"><stop offset="0.138435" stop-color="#FFB974"></stop><stop offset="0.403618" stop-color="#F2A56D"></stop><stop offset="0.925938" stop-color="#A16948"></stop></radialGradient><linearGradient id="paint13_linear_18_31665" x1="8.22184" y1="13.125" x2="6.81191" y2="15.4996" gradientUnits="userSpaceOnUse"><stop offset="0.610751" stop-color="#984847"></stop><stop offset="0.850075" stop-color="#9A4947" stop-opacity="0"></stop></linearGradient><radialGradient id="paint14_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(7.25 23.7461) scale(11.25 5.68361)"><stop stop-color="#C66364"></stop><stop offset="1" stop-color="#D4766B" stop-opacity="0"></stop></radialGradient><radialGradient id="paint15_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(7.875 23.5313) scale(10.0937 1.29657)"><stop stop-color="#B64B4B"></stop><stop offset="1" stop-color="#C56158" stop-opacity="0"></stop></radialGradient><radialGradient id="paint16_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(11.4375 19.875) rotate(-46.8882) scale(4.02385 7.51767)"><stop stop-color="#FFC083"></stop><stop offset="0.620218" stop-color="#FFBD7D" stop-opacity="0"></stop></radialGradient><linearGradient id="paint17_linear_18_31665" x1="2.8125" y1="13.0312" x2="14.5582" y2="18.9404" gradientUnits="userSpaceOnUse"><stop stop-color="#B89367"></stop><stop offset="1" stop-color="#C5835E"></stop></linearGradient><linearGradient id="paint18_linear_18_31665" x1="8.21875" y1="14.6406" x2="7.59349" y2="15.6717" gradientUnits="userSpaceOnUse"><stop offset="0.351552" stop-color="#A74746"></stop><stop offset="0.845198" stop-color="#A04346" stop-opacity="0"></stop></linearGradient><radialGradient id="paint19_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(15.5625 14.5625) rotate(140.244) scale(18.3733 13.7403)"><stop stop-color="#FDAE69"></stop><stop offset="0.729021" stop-color="#CE8C4F"></stop><stop offset="0.921546" stop-color="#AD7B45"></stop><stop offset="1" stop-color="#8B6B4A"></stop></radialGradient><radialGradient id="paint20_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(15.0625 7) rotate(65.3152) scale(11.0745 3.16547)"><stop offset="0.233237" stop-color="#FFD47C"></stop><stop offset="0.853648" stop-color="#FFD98B" stop-opacity="0"></stop></radialGradient><radialGradient id="paint21_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(15.3125 8.875) rotate(100.886) scale(6.6191 5.57808)"><stop offset="0.128419" stop-color="#FFD88C"></stop><stop offset="0.924134" stop-color="#FFBE7B" stop-opacity="0"></stop></radialGradient><linearGradient id="paint22_linear_18_31665" x1="7.25" y1="15.1875" x2="10.7588" y2="10.3142" gradientUnits="userSpaceOnUse"><stop offset="0.142353" stop-color="#C15F4D"></stop><stop offset="1" stop-color="#D58366" stop-opacity="0"></stop></linearGradient><radialGradient id="paint23_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(8.15625 15.7813) rotate(28.5422) scale(12.5574 1.96589)"><stop offset="0.149989" stop-color="#E4745D"></stop><stop offset="0.453292" stop-color="#C8604C"></stop><stop offset="0.632597" stop-color="#C0605F"></stop><stop offset="1" stop-color="#C0605F" stop-opacity="0"></stop></radialGradient><radialGradient id="paint24_radial_18_31665" cx="0" cy="0" r="1" gradientUnits="userSpaceOnUse" gradientTransform="translate(1.40625 2.69067) rotate(46.0943) scale(22.3963)"><stop offset="0.935802" stop-color="#C17C61" stop-opacity="0"></stop><stop offset="0.982109" stop-color="#C17C61"></stop></radialGradient></defs></svg> <span>Croissant</span> <div class="border-br-gray-200 absolute bottom-0.5 right-0.5 h-1 w-1 border-[3px] border-l-transparent border-t-transparent border-b-gray-200 border-r-gray-200 dark:border-b-gray-700 dark:border-r-gray-700"></div></div> </button> </div> <button class="tag tag-ghost -ml-0.5 mb-1 !px-1 md:mb-1.5" type="button">+ 1</button></div><div class="mr-1 flex flex-wrap items-center"><span class="mb-1 mr-1 p-1 text-sm leading-tight text-gray-400 md:mb-1.5">License: </span> <div class="relative inline-block "> <button class="group mr-1 mb-1 md:mr-1.5 md:mb-1.5 rounded-full rounded-br-none " type="button"> <div class="tag tag-white rounded-full relative rounded-br-none pr-2.5"> <svg class="text-xs text-gray-900" width="1em" height="1em" viewBox="0 0 10 10" fill="none" xmlns="http://www.w3.org/2000/svg"><path d="M1.46009 5.0945V6.88125C1.46009 7.25201 1.75937 7.55129 2.13012 7.55129C2.50087 7.55129 2.80016 7.25201 2.80016 6.88125V5.0945C2.80016 4.72375 2.50087 4.42446 2.13012 4.42446C1.75937 4.42446 1.46009 4.72375 1.46009 5.0945ZM4.14022 5.0945V6.88125C4.14022 7.25201 4.4395 7.55129 4.81026 7.55129C5.18101 7.55129 5.48029 7.25201 5.48029 6.88125V5.0945C5.48029 4.72375 5.18101 4.42446 4.81026 4.42446C4.4395 4.42446 4.14022 4.72375 4.14022 5.0945ZM1.23674 9.78473H8.38377C8.75452 9.78473 9.0538 9.48545 9.0538 9.1147C9.0538 8.74395 8.75452 8.44466 8.38377 8.44466H1.23674C0.865993 8.44466 0.566711 8.74395 0.566711 9.1147C0.566711 9.48545 0.865993 9.78473 1.23674 9.78473ZM6.82036 5.0945V6.88125C6.82036 7.25201 7.11964 7.55129 7.49039 7.55129C7.86114 7.55129 8.16042 7.25201 8.16042 6.88125V5.0945C8.16042 4.72375 7.86114 4.42446 7.49039 4.42446C7.11964 4.42446 6.82036 4.72375 6.82036 5.0945ZM4.39484 0.623142L0.865993 2.48137C0.682851 2.57517 0.566711 2.76725 0.566711 2.97273C0.566711 3.28094 0.816857 3.53109 1.12507 3.53109H8.49991C8.80365 3.53109 9.0538 3.28094 9.0538 2.97273C9.0538 2.76725 8.93766 2.57517 8.75452 2.48137L5.22568 0.623142C4.9666 0.484669 4.65391 0.484669 4.39484 0.623142V0.623142Z" fill="currentColor"></path></svg> <span>apache-2.0</span> <div class="border-br-gray-200 absolute bottom-0.5 right-0.5 h-1 w-1 border-[3px] border-l-transparent border-t-transparent border-b-gray-200 border-r-gray-200 dark:border-b-gray-700 dark:border-r-gray-700"></div></div> </button> </div> </div></div> <div class="flex flex-col-reverse lg:flex-row lg:items-center lg:justify-between"><div class="-mb-px flex h-12 items-center overflow-x-auto overflow-y-hidden "><a class="tab-alternate active" href="/datasets/AI-MO/NuminaMath-1.5"><svg class="mr-1.5 text-gray-400 flex-none" style="" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 24 24"><path class="uim-quaternary" d="M20.23 7.24L12 12L3.77 7.24a1.98 1.98 0 0 1 .7-.71L11 2.76c.62-.35 1.38-.35 2 0l6.53 3.77c.29.173.531.418.7.71z" opacity=".25" fill="currentColor"></path><path class="uim-tertiary" d="M12 12v9.5a2.09 2.09 0 0 1-.91-.21L4.5 17.48a2.003 2.003 0 0 1-1-1.73v-7.5a2.06 2.06 0 0 1 .27-1.01L12 12z" opacity=".5" fill="currentColor"></path><path class="uim-primary" d="M20.5 8.25v7.5a2.003 2.003 0 0 1-1 1.73l-6.62 3.82c-.275.13-.576.198-.88.2V12l8.23-4.76c.175.308.268.656.27 1.01z" fill="currentColor"></path></svg> Dataset card </a><a class="tab-alternate " href="/datasets/AI-MO/NuminaMath-1.5/viewer/"><svg class="mr-1.5 text-gray-400 flex-none" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 12 12"><path fill="currentColor" d="M2.5 2h7a1 1 0 0 1 1 1v6a1 1 0 0 1-1 1h-7a1 1 0 0 1-1-1V3a1 1 0 0 1 1-1Zm0 2v2h3V4h-3Zm4 0v2h3V4h-3Zm-4 3v2h3V7h-3Zm4 0v2h3V7h-3Z"></path></svg> Viewer </a><a class="tab-alternate " href="/datasets/AI-MO/NuminaMath-1.5/tree/main"><svg class="mr-1.5 text-gray-400 flex-none" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 24 24"><path class="uim-tertiary" d="M21 19h-8a1 1 0 0 1 0-2h8a1 1 0 0 1 0 2zm0-4h-8a1 1 0 0 1 0-2h8a1 1 0 0 1 0 2zm0-8h-8a1 1 0 0 1 0-2h8a1 1 0 0 1 0 2zm0 4h-8a1 1 0 0 1 0-2h8a1 1 0 0 1 0 2z" opacity=".5" fill="currentColor"></path><path class="uim-primary" d="M9 19a1 1 0 0 1-1-1V6a1 1 0 0 1 2 0v12a1 1 0 0 1-1 1zm-6-4.333a1 1 0 0 1-.64-1.769L3.438 12l-1.078-.898a1 1 0 0 1 1.28-1.538l2 1.667a1 1 0 0 1 0 1.538l-2 1.667a.999.999 0 0 1-.64.231z" fill="currentColor"></path></svg> <span class="xl:hidden">Files</span> <span class="hidden xl:inline">Files and versions</span> </a><a class="tab-alternate " href="/datasets/AI-MO/NuminaMath-1.5/discussions"><svg class="mr-1.5 text-gray-400 flex-none" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32"><path d="M20.6081 3C21.7684 3 22.8053 3.49196 23.5284 4.38415C23.9756 4.93678 24.4428 5.82749 24.4808 7.16133C24.9674 7.01707 25.4353 6.93643 25.8725 6.93643C26.9833 6.93643 27.9865 7.37587 28.696 8.17411C29.6075 9.19872 30.0124 10.4579 29.8361 11.7177C29.7523 12.3177 29.5581 12.8555 29.2678 13.3534C29.8798 13.8646 30.3306 14.5763 30.5485 15.4322C30.719 16.1032 30.8939 17.5006 29.9808 18.9403C30.0389 19.0342 30.0934 19.1319 30.1442 19.2318C30.6932 20.3074 30.7283 21.5229 30.2439 22.6548C29.5093 24.3704 27.6841 25.7219 24.1397 27.1727C21.9347 28.0753 19.9174 28.6523 19.8994 28.6575C16.9842 29.4379 14.3477 29.8345 12.0653 29.8345C7.87017 29.8345 4.8668 28.508 3.13831 25.8921C0.356375 21.6797 0.754104 17.8269 4.35369 14.1131C6.34591 12.058 7.67023 9.02782 7.94613 8.36275C8.50224 6.39343 9.97271 4.20438 12.4172 4.20438H12.4179C12.6236 4.20438 12.8314 4.2214 13.0364 4.25468C14.107 4.42854 15.0428 5.06476 15.7115 6.02205C16.4331 5.09583 17.134 4.359 17.7682 3.94323C18.7242 3.31737 19.6794 3 20.6081 3ZM20.6081 5.95917C20.2427 5.95917 19.7963 6.1197 19.3039 6.44225C17.7754 7.44319 14.8258 12.6772 13.7458 14.7131C13.3839 15.3952 12.7655 15.6837 12.2086 15.6837C11.1036 15.6837 10.2408 14.5497 12.1076 13.1085C14.9146 10.9402 13.9299 7.39584 12.5898 7.1776C12.5311 7.16799 12.4731 7.16355 12.4172 7.16355C11.1989 7.16355 10.6615 9.33114 10.6615 9.33114C10.6615 9.33114 9.0863 13.4148 6.38031 16.206C3.67434 18.998 3.5346 21.2388 5.50675 24.2246C6.85185 26.2606 9.42666 26.8753 12.0653 26.8753C14.8021 26.8753 17.6077 26.2139 19.1799 25.793C19.2574 25.7723 28.8193 22.984 27.6081 20.6107C27.4046 20.212 27.0693 20.0522 26.6471 20.0522C24.9416 20.0522 21.8393 22.6726 20.5057 22.6726C20.2076 22.6726 19.9976 22.5416 19.9116 22.222C19.3433 20.1173 28.552 19.2325 27.7758 16.1839C27.639 15.6445 27.2677 15.4256 26.746 15.4263C24.4923 15.4263 19.4358 19.5181 18.3759 19.5181C18.2949 19.5181 18.2368 19.4937 18.2053 19.4419C17.6743 18.557 17.9653 17.9394 21.7082 15.6009C25.4511 13.2617 28.0783 11.8545 26.5841 10.1752C26.4121 9.98141 26.1684 9.8956 25.8725 9.8956C23.6001 9.89634 18.2311 14.9403 18.2311 14.9403C18.2311 14.9403 16.7821 16.496 15.9057 16.496C15.7043 16.496 15.533 16.4139 15.4169 16.2112C14.7956 15.1296 21.1879 10.1286 21.5484 8.06535C21.7928 6.66715 21.3771 5.95917 20.6081 5.95917Z" fill="#FF9D00"></path><path d="M5.50686 24.2246C3.53472 21.2387 3.67446 18.9979 6.38043 16.206C9.08641 13.4147 10.6615 9.33111 10.6615 9.33111C10.6615 9.33111 11.2499 6.95933 12.59 7.17757C13.93 7.39581 14.9139 10.9401 12.1069 13.1084C9.29997 15.276 12.6659 16.7489 13.7459 14.713C14.8258 12.6772 17.7747 7.44316 19.304 6.44221C20.8326 5.44128 21.9089 6.00204 21.5484 8.06532C21.188 10.1286 14.795 15.1295 15.4171 16.2118C16.0391 17.2934 18.2312 14.9402 18.2312 14.9402C18.2312 14.9402 25.0907 8.49588 26.5842 10.1752C28.0776 11.8545 25.4512 13.2616 21.7082 15.6008C17.9646 17.9393 17.6744 18.557 18.2054 19.4418C18.7372 20.3266 26.9998 13.1351 27.7759 16.1838C28.5513 19.2324 19.3434 20.1173 19.9117 22.2219C20.48 24.3274 26.3979 18.2382 27.6082 20.6107C28.8193 22.9839 19.2574 25.7722 19.18 25.7929C16.0914 26.62 8.24723 28.3726 5.50686 24.2246Z" fill="#FFD21E"></path></svg> Community <div class="ml-1.5 flex h-4 min-w-[1rem] items-center justify-center rounded px-1 text-xs leading-none shadow-sm bg-black text-white dark:bg-gray-800 dark:text-gray-200">3 </div> </a> </div> </div></div></header> </div> <div class="container relative flex flex-col md:grid md:space-y-0 w-full md:grid-cols-12 md:flex-1 md:grid-rows-full space-y-4 md:gap-6 "> <section class="pt-6 border-gray-100 md:col-span-8 pb-24 relative break-words copiable-code-container"><div class="SVELTE_HYDRATER contents" data-target="UnsafeBanner" data-props="{"classNames":"mb-4","repoId":"AI-MO/NuminaMath-1.5","repoType":"dataset","minLevel":"unsafe"}"></div> <div class="SVELTE_HYDRATER contents" data-target="DatasetViewer" data-props="{"data":{"kind":"DatasetAndSampleData","datasetInfo":[{"isValid":true,"href":"","label":"Size of downloaded dataset files:","value":"531 MB"},{"isValid":true,"href":"/datasets/AI-MO/NuminaMath-1.5/tree/refs%2Fconvert%2Fparquet/","label":"Size of the auto-converted Parquet files:","value":"531 MB"},{"isValid":true,"href":"","label":"Number of rows:","value":"896,215"}],"partial":false,"configsData":{"configInfos":[{"name":"default","status":"ok","numRows":896215}],"selectedConfig":"default","hasSelectedConfigParquet":true},"splitsData":{"splitInfos":[{"name":"train","numRows":896215}],"selectedSplit":"train"},"sampleData":{"dataset":"AI-MO/NuminaMath-1.5","config":"default","split":"train","capabilities":{"rows":true,"search":true,"filter":true,"statistics":true},"navigation":{"p":0},"jwt":"eyJhbGciOiJFZERTQSJ9.eyJyZWFkIjp0cnVlLCJwZXJtaXNzaW9ucyI6eyJyZXBvLmNvbnRlbnQucmVhZCI6dHJ1ZX0sImlhdCI6MTc0MDE1Nzc2NSwic3ViIjoiL2RhdGFzZXRzL0FJLU1PL051bWluYU1hdGgtMS41IiwiZXhwIjoxNzQwMTYxMzY1LCJpc3MiOiJodHRwczovL2h1Z2dpbmdmYWNlLmNvIn0.60e04HFdn4xdNBalzpbXAtkTs0ycYnHKsbuw5jZ-PTFKkGymswloGMXyb59KxxGpkjHf9yM4NmqyppI4D3nNCg","sampleData":{"columns":[{"name":"problem","align":"depends on text direction","type":"string","statistics":{"column_name":"problem","column_type":"string_text","column_statistics":{"nan_count":0,"nan_proportion":0,"min":0,"max":45303,"mean":262.34615,"median":216,"std":265.74025,"histogram":{"hist":[895927,242,18,13,4,2,3,1,4,1],"bin_edges":[0,4531,9062,13593,18124,22655,27186,31717,36248,40779,45303]}}}},{"name":"solution","align":"depends on text direction","type":"string","statistics":{"column_name":"solution","column_type":"string_text","column_statistics":{"nan_count":32428,"nan_proportion":0.03618,"min":0,"max":26844,"mean":965.03045,"median":807,"std":724.79689,"histogram":{"hist":[840275,21391,1832,233,43,7,3,2,0,1],"bin_edges":[0,2685,5370,8055,10740,13425,16110,18795,21480,24165,26844]}}}},{"name":"answer","align":"depends on text direction","type":"string","statistics":{"column_name":"answer","column_type":"string_text","column_statistics":{"nan_count":51408,"nan_proportion":0.05736,"min":0,"max":575,"mean":9.10886,"median":5,"std":14.33215,"histogram":{"hist":[830569,12255,1747,188,23,13,6,1,4,1],"bin_edges":[0,58,116,174,232,290,348,406,464,522,575]}}}},{"name":"problem_type","align":"depends on text direction","type":"string","statistics":{"column_name":"problem_type","column_type":"string_label","column_statistics":{"nan_count":0,"nan_proportion":0,"no_label_count":0,"no_label_proportion":0,"n_unique":9,"frequencies":{"Logic and Puzzles":37911,"Geometry":183796,"Calculus":26965,"Algebra":422915,"Combinatorics":73643,"Number Theory":91383,"Other":12645,"Inequalities":41741,"NaN":5216}}}},{"name":"question_type","align":"depends on text direction","type":"string","statistics":{"column_name":"question_type","column_type":"string_label","column_statistics":{"nan_count":0,"nan_proportion":0,"no_label_count":0,"no_label_proportion":0,"n_unique":5,"frequencies":{"proof":110998,"other":2030,"NaN":5216,"math-word-problem":631522,"MCQ":146449}}}},{"name":"problem_is_valid","align":"depends on text direction","type":"string","statistics":{"column_name":"problem_is_valid","column_type":"string_label","column_statistics":{"nan_count":0,"nan_proportion":0,"no_label_count":0,"no_label_proportion":0,"n_unique":5,"frequencies":{"Incomplete":30377,"Yes":859356,"NaN":5219,"Not a problem":158,"More than one problem":1105}}}},{"name":"solution_is_valid","align":"depends on text direction","type":"string","statistics":{"column_name":"solution_is_valid","column_type":"string_label","column_statistics":{"nan_count":0,"nan_proportion":0,"no_label_count":0,"no_label_proportion":0,"n_unique":5,"frequencies":{"Yes":844988,"Problem not solved":13446,"NaN":5227,"Incomplete":32522,"Not matched with problem":32}}}},{"name":"source","align":"depends on text direction","type":"string","statistics":{"column_name":"source","column_type":"string_label","column_statistics":{"nan_count":0,"nan_proportion":0,"no_label_count":0,"no_label_proportion":0,"n_unique":11,"frequencies":{"aops_forum":67841,"olympiads_ref":3638,"number_theory":4043,"synthetic_math":148712,"orca_math":151934,"inequalities":7314,"cn_contest":29944,"olympiads":197084,"metamath":11014,"amc_aime":5872,"cn_k12":268819}}}},{"name":"synthetic","align":"right","type":"bool","statistics":{"column_name":"synthetic","column_type":"bool","column_statistics":{"nan_count":0,"nan_proportion":0,"frequencies":{"False":584555,"True":311660}}}}],"rows":[{"rowIdx":0,"cells":{"problem":{"kind":"string","value":"\nProblem 1. Find all prime numbers $p$ for which there exist positive integers $x, y$ and $z$ such that the number\n\n$$\nx^{p}+y^{p}+z^{p}-x-y-z\n$$\n\nis a product of exactly three distinct prime numbers.\n"},"solution":{"kind":"string","value":"\nSolution. Let $A=x^{p}+y^{p}+z^{p}-x-y-z$. For $p=2$, we take $x=y=4$ and $z=3$. Then $A=30=2 \\cdot 3 \\cdot 5$. For $p=3$ we can take $x=3$ and $y=2$ and $z=1$. Then again $A=30=2 \\cdot 3 \\cdot 5$. For $p=5$ we can take $x=2$ and $y=1$ and $z=1$. Again $A=30=2 \\cdot 3 \\cdot 5$.\n\nAssume now that $p \\geqslant 7$. Working modulo 2 and modulo 3 we see that $A$ is divisible by both 2 and 3. Moreover, by Fermat's Little Theorem, we have\n\n$$\nx^{p}+y^{p}+z^{p}-x-y-z \\equiv x+y+z-x-y-z=0 \\bmod p \\text {. }\n$$\n\nTherefore, by the given condition, we have to solve the equation\n\n$$\nx^{p}+y^{p}+z^{p}-x-y-z=6 p\n$$\n\nIf one of the numbers $x, y$ and $z$ is bigger than or equal to 2 , let's say $x \\geqslant 2$, then\n\n$$\n6 p \\geqslant x^{p}-x=x\\left(x^{p-1}-1\\right) \\geqslant 2\\left(2^{p-1}-1\\right)=2^{p}-2\n$$\n\nIt is easy to check by induction that $2^{n}-2>6 n$ for all natural numbers $n \\geqslant 6$. This contradiction shows that there are no more values of $p$ which satisfy the required property.\n\nRemark. There are a couple of other ways to prove that $2^{p}-2>6 p$ for $p \\geqslant 7$. For example, we can use the Binomial Theorem as follows:\n\n$$\n2^{p}-2 \\geqslant 1+p+\\frac{p(p-1)}{2}+\\frac{p(p-1)(p-2)}{6}-2 \\geqslant 1+p+3 p+5 p-2>6 p\n$$\n\nWe can also use Bernoulli's Inequality as follows:\n\n$$\n2^{p}-2=8(1+1)^{p-3}-2 \\geqslant 8(1+(p-3))-2=8 p-18>6 p\n$$\n\nThe last inequality is true for $p \\geqslant 11$. For $p=7$ we can see directly that $2^{p}-2>6 p$.\n\nOne can also use calculus to show that $f(x)=2^{x}-6 x$ is increasing for $x \\geqslant 5$.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":1,"cells":{"problem":{"kind":"string","value":"\nProblem 2. Let $a, b$ be two distinct real numbers and let $c$ be a positive real number such that\n\n$$\na^{4}-2019 a=b^{4}-2019 b=c .\n$$\n\nProve that $-\\sqrt{c}<a b<0$.\n"},"solution":{"kind":"string","value":"\nSolution. Firstly, we see that\n\n$$\n2019(a-b)=a^{4}-b^{4}=(a-b)(a+b)\\left(a^{2}+b^{2}\\right)\n$$\n\nSince $a \\neq b$, we get $(a+b)\\left(a^{2}+b^{2}\\right)=2019$, so $a+b \\neq 0$. Thus\n\n$$\n\\begin{aligned}\n2 c & =a^{4}-2019 a+b^{4}-2019 b \\\\\n& =a^{4}+b^{4}-2019(a+b) \\\\\n& =a^{4}+b^{4}-(a+b)^{2}\\left(a^{2}+b^{2}\\right) \\\\\n& =-2 a b\\left(a^{2}+a b+b^{2}\\right)\n\\end{aligned}\n$$\n\nHence $a b\\left(a^{2}+a b+b^{2}\\right)=-c0\n$$\n\nthus $a b-a b$ (the equality does not occur since $a+b \\neq 0$ ). So\n\n$$\n-c=a b\\left(a^{2}+a b+b^{2}\\right)<-(a b)^{2} \\Longrightarrow(a b)^{2}<c \\Rightarrow-\\sqrt{c}<a b<\\sqrt{c}\n$$\n\nTherefore, we have $-\\sqrt{c}<a b<0$.\n\nRemark. We can get $c=-a b\\left(a^{2}+a b+b^{2}\\right)$ in several other ways. For example using that,\n\n$$\n(a-b) c=a\\left(b^{4}-2019 b\\right)-b\\left(a^{4}-2019 a\\right)=a b\\left(b^{3}-a^{3}\\right)=a b(b-a)\\left(a^{2}+a b+b^{2}\\right)\n$$\n\nWe can also divide $f(x)=x^{4}-2019 x-c$ by $(x-a)(x-b)$ and look at the constant term of the remainder.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Algebra"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Incomplete"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":2,"cells":{"problem":{"kind":"string","value":"\nProblem 3. Triangle $A B C$ is such that $A B<A C$. The perpendicular bisector of side $B C$ intersects lines $A B$ and $A C$ at points $P$ and $Q$, respectively. Let $H$ be the orthocentre of triangle $A B C$, and let $M$ and $N$ be the midpoints of segments $B C$ and $P Q$, respectively. Prove that lines $H M$ and $A N$ meet on the circumcircle of $A B C$.\n"},"solution":{"kind":"string","value":"\nSolution. We have\n\n$$\n\\angle A P Q=\\angle B P M=90^{\\circ}-\\angle M B P=90^{\\circ}-\\angle C B A=\\angle H C B\n$$\n\nand\n\n$$\n\\angle A Q P=\\angle M Q C=90^{\\circ}-\\angle Q C M=90^{\\circ}-\\angle A C B=\\angle C B H\n$$\n\nFrom these two equalities, we see that the triangles $A P Q$ and $H C B$ are similar. Moreover, since $M$ and $N$ are the midpoints of the segments $B C$ and $P Q$ respectively, then the triangles $A Q N$ and $H B M$ are also similar. Therefore, we have $\\angle A N Q=\\angle H M B$.\n\n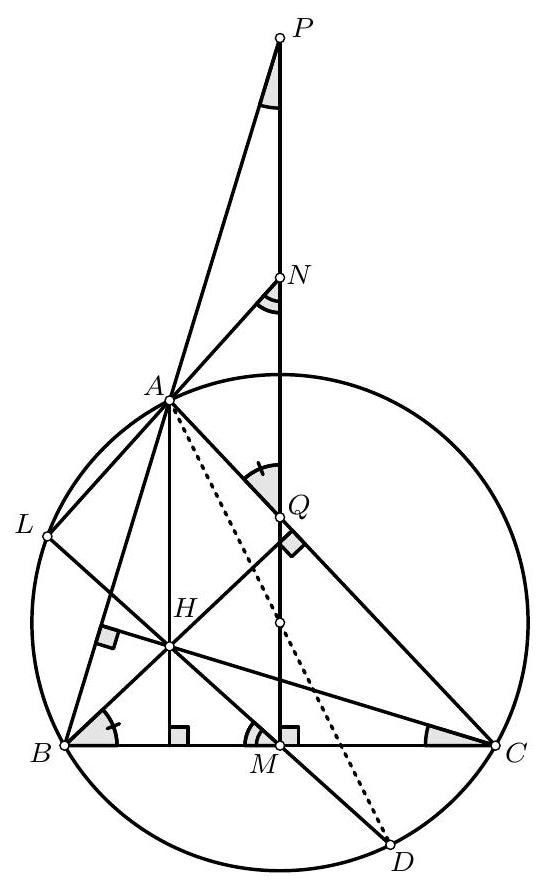![](https://cdn.mathpix.com/cropped/2024_06_05_fe2687448771fc19bd4eg-4.jpg?height=883&width=545&top_left_y=865&top_left_x=779)\n\nLet $L$ be the intersection of $A N$ and $H M$. We have\n\n$$\n\\angle M L N=180^{\\circ}-\\angle L N M-\\angle N M L=180^{\\circ}-\\angle L M B-\\angle N M L=180^{\\circ}-\\angle N M B=90^{\\circ} .\n$$\n\nNow let $D$ be the point on the circumcircle of $A B C$ diametrically oposite to $A$. It is known that $D$ is also the relfection of point $H$ over the point $M$. Therefore, we have that $D$ belongs on $M H$ and that $\\angle D L A=\\angle M L A=\\angle M L N=90^{\\circ}$. But, as $D A$ is the diameter of the circumcirle of $A B C$, the condition that $\\angle D L A=90^{\\circ}$ is enough to conclude that $L$ belongs on the circumcircle of $A B C$.\n\nRemark. There is a spiral similarity mapping $A Q P$ to $H B C$. Since the similarity maps $A N$ to $H M$, it also maps $A H$ to $N M$, and since these two lines are parallel, the centre of the similarity is $L=A N \\cap H M$. Since the similarity maps $B C$ to $Q P$, its centre belongs on the circumcircle of $B C X$, where $X=B Q \\cap P C$. But $X$ is the reflection of $A$ on $Q M$ and so it must belong on the circumcircle of $A B C$. Hence so must $L$.\n\nRemark. Students have also submitted correct proofs using radical axes, harmonic quadruples, coordinate geometry and complex numbers.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":3,"cells":{"problem":{"kind":"string","value":"\nProblem 4. A $5 \\times 100$ table is divided into 500 unit square cells, where $n$ of them are coloured black and the rest are coloured white. Two unit square cells are called adjacent if they share a common side. Each of the unit square cells has at most two adjacent black unit square cells. Find the largest possible value of $n$.\n"},"solution":{"kind":"string","value":"\nSolution. If we colour all the cells along all edges of the board together with the entire middle row except the second and the last-but-one cell, the condition is satisfied and there are 302 black cells. The figure below exhibits this colouring for the $5 \\times 8$ case.\n\n![](https://cdn.mathpix.com/cropped/2024_06_05_fe2687448771fc19bd4eg-5.jpg?height=320&width=493&top_left_y=629&top_left_x=816)\n\nWe can cover the table by one fragment like the first one on the figure below, 24 fragments like the middle one, and one fragment like the third one.\n\n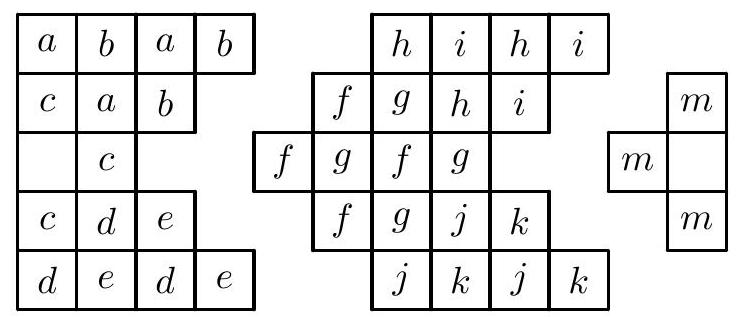![](https://cdn.mathpix.com/cropped/2024_06_05_fe2687448771fc19bd4eg-5.jpg?height=317&width=737&top_left_y=1132&top_left_x=694)\n\nIn each fragment, among the cells with the same letter, there are at most two coloured black, so the total number of coloured cells is at most $(5+24 \\cdot 6+1) \\cdot 2+2=302$.\n"},"answer":{"kind":"string","value":"302"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":4,"cells":{"problem":{"kind":"string","value":"\nProblem 1. A trapezoid $A B C D(A B \\| C D, A B>C D)$ is circumscribed. The incircle of the triangle $A B C$ touches the lines $A B$ and $A C$ at the points $M$ and $N$, respectively. Prove that the incenter of the trapezoid $A B C D$ lies on the line $M N$.\n\n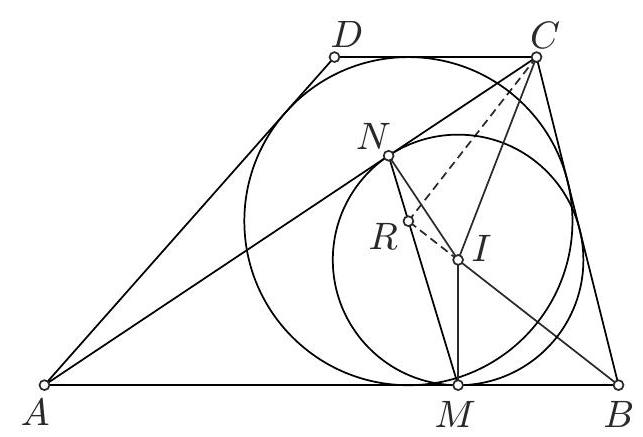![](https://cdn.mathpix.com/cropped/2024_06_05_bc5716af31e6d23d397cg-1.jpg?height=437&width=643&top_left_y=752&top_left_x=661)\n\n"},"solution":{"kind":"string","value":"## Solution.\n\nVersion 1. Let $I$ be the incenter of triangle $A B C$ and $R$ be the common point of the lines $B I$ and $M N$. Since\n\n$$\nm(\\widehat{A N M})=90^{\\circ}-\\frac{1}{2} m(\\widehat{M A N}) \\quad \\text { and } \\quad m(\\widehat{B I C})=90^{\\circ}+\\frac{1}{2} m(\\widehat{M A N})\n$$\n\nthe quadrilateral $I R N C$ is cyclic.\n\nIt follows that $m(\\widehat{B R C})=90^{\\circ}$ and therefore\n\n$$\nm(\\widehat{B C R})=90^{\\circ}-m(\\widehat{C B R})=90^{\\circ}-\\frac{1}{2}\\left(180^{\\circ}-m(\\widehat{B C D})\\right)=\\frac{1}{2} m(\\widehat{B C D})\n$$\n\nSo, $(C R$ is the angle bisector of $\\widehat{D C B}$ and $R$ is the incenter of the trapezoid.\n\nVersion 2. If $R$ is the incentre of the trapezoid $A B C D$, then $B, I$ and $R$ are collinear,\n\nand $m(\\widehat{B R C})=90^{\\circ}$.\n\nThe quadrilateral $I R N C$ is cyclic.\n\nThen $m(\\widehat{M N C})=90^{\\circ}+\\frac{1}{2} \\cdot m(\\widehat{B A C})$\n\nand $m(\\widehat{R N C})=m(\\widehat{B I C})=90^{\\circ}+\\frac{1}{2} \\cdot m(\\widehat{B A C})$,\nso that $m(\\widehat{M N C})=m(\\widehat{R N C})$ and the points $M, R$ and $N$ are collinear.\n\nVersion 3. If $R$ is the incentre of the trapezoid $A B C D$, let $M^{\\prime} \\in(A B)$ and $N^{\\prime} \\in(A C)$ be the unique points, such that $R \\in M^{\\prime} N^{\\prime}$ and $\\left(A M^{\\prime}\\right) \\equiv\\left(A N^{\\prime}\\right)$.\n\nLet $S$ be the intersection point of $C R$ and $A B$. Then $C R=R S$.\n\nConsider $K \\in A C$ such that $S K \\| M^{\\prime} N^{\\prime}$. Then $N^{\\prime}$ is the midpoint of $(C K)$.\n\nWe deduce\n\n$$\nA N^{\\prime}=\\frac{A K+A C}{2}=\\frac{A S+A C}{2}=\\frac{A B-B S+A C}{2}=\\frac{A B+A C-B C}{2}=A N\n$$\n\nWe conclude that $N=N^{\\prime}$, hence $M=M^{\\prime}$, and $R, M, N$ are collinear.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":5,"cells":{"problem":{"kind":"string","value":"\nProblem 2. Let $a, b$ and $c$ be positive real numbers. Prove that\n\n$$\n\\frac{8}{(a+b)^{2}+4 a b c}+\\frac{8}{(b+c)^{2}+4 a b c}+\\frac{8}{(c+a)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \\geq \\frac{8}{a+3}+\\frac{8}{b+3}+\\frac{8}{c+3}\n$$\n"},"solution":{"kind":"string","value":"\nSolution. Since $2 a b \\leq a^{2}+b^{2}$, it follows that $(a+b)^{2} \\leq 2\\left(a^{2}+b^{2}\\right)$\n\nand $4 a b c \\leq 2 c\\left(a^{2}+b^{2}\\right)$, for any positive reals $a, b, c$.\n\nAdding these inequalities, we find\n\n$$\n(a+b)^{2}+4 a b c \\leq 2\\left(a^{2}+b^{2}\\right)(c+1)\n$$\n\nso that\n\n$$\n\\frac{8}{(a+b)^{2}+4 a b c} \\geq \\frac{4}{\\left(a^{2}+b^{2}\\right)(c+1)}\n$$\n\nUsing the AM-GM inequality, we have\n\n$$\n\\frac{4}{\\left(a^{2}+b^{2}\\right)(c+1)}+\\frac{a^{2}+b^{2}}{2} \\geq 2 \\sqrt{\\frac{2}{c+1}}=\\frac{4}{\\sqrt{2(c+1)}}\n$$\n\nrespectively\n\n$$\n\\frac{c+3}{8}=\\frac{(c+1)+2}{8} \\geq \\frac{\\sqrt{2(c+1)}}{4}\n$$\n\nWe conclude that\n\n$$\n\\frac{4}{\\left(a^{2}+b^{2}\\right)(c+1)}+\\frac{a^{2}+b^{2}}{2} \\geq \\frac{8}{c+3}\n$$\n\nand finally\n\n$$\n\\frac{8}{(a+b)^{2}+4 a b c}+\\frac{8}{(a+c)^{2}+4 a b c}+\\frac{8}{(b+c)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \\geq \\frac{8}{a+3}+\\frac{8}{b+3}+\\frac{8}{c+3}\n$$\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":6,"cells":{"problem":{"kind":"string","value":"\nProblem 3. Find all the triples of integers $(a, b, c)$ such that the number\n\n$$\nN=\\frac{(a-b)(b-c)(c-a)}{2}+2\n$$\n\nis a power of 2016 .\n\n(A power of 2016 is an integer of the form $2016^{n}$, where $n$ is a non-negative integer.)\n"},"solution":{"kind":"string","value":"\nSolution. Let $a, b, c$ be integers and $n$ be a positive integer such that\n\n$$\n(a-b)(b-c)(c-a)+4=2 \\cdot 2016^{n}\n$$\n\nWe set $a-b=-x, b-c=-y$ and we rewrite the equation as\n\n$$\nx y(x+y)+4=2 \\cdot 2016^{n}\n$$\n\nIf $n>0$, then the right hand side is divisible by 7 , so we have that\n\n$$\nx y(x+y)+4 \\equiv 0 \\quad(\\bmod 7)\n$$\n\nor\n\n$$\n3 x y(x+y) \\equiv 2 \\quad(\\bmod 7)\n$$\n\nor\n\n$$\n(x+y)^{3}-x^{3}-y^{3} \\equiv 2 \\quad(\\bmod 7)\n$$\n\nNote that, by Fermat's Little Theorem, for any integer $k$ the cubic residues are $k^{3} \\equiv-1,0,1$ $(\\bmod 7)$.\n\nIt follows that in (1) some of $(x+y)^{3}, x^{3}$ and $y^{3}$ should be divisible by 7 .\n\nBut in this case, $x y(x+y)$ is divisible by 7 and this is a contradiction.\n\nSo, the only possibility is to have $n=0$ and consequently, $x y(x+y)+4=2$, or, equivalently, $x y(x+y)=-2$.\n\nThe solutions for this are $(x, y) \\in\\{(-1,-1),(2,-1),(-1,2)\\}$,\n\nso the required triples are $(a, b, c)=(k+2, k+1, k), k \\in \\mathbb{Z}$, and all their cyclic permutations. (9)\n\nAlternative version: If $n>0$ then 9 divides $(a-b)(b-c)(c-a)+4$, that is, the equation $x y(x+y)+4 \\equiv 0(\\bmod 9))$ has the solution $x=b-a, y=c-b$.\n\nBut then $x$ and $y$ have to be 1 modulo 3 , implying $x y(x+y) \\equiv 2(\\bmod 9)$, which is a contradiction.\n\nWe can continue now as in the first version.\n"},"answer":{"kind":"string","value":"(,b,)=(k+2,k+1,k),k\\in\\mathbb{Z}"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":7,"cells":{"problem":{"kind":"string","value":"\nProblem 2. Let $n$ three-digit numbers satisfy the following properties:\n\n(1) No number contains the digit 0 .\n\n(2) The sum of the digits of each number is 9 .\n\n(3) The units digits of any two numbers are different.\n\n(4) The tens digits of any two numbers are different.\n\n(5) The hundreds digits of any two numbers are different.\n\nFind the largest possible value of $n$.\n"},"solution":{"kind":"string","value":"\nSolution. Let $S$ denote the set of three-digit numbers that have digit sum equal to 9 and no digit equal to 0 . We will first find the cardinality of $S$. We start from the number 111 and each element of $S$ can be obtained from 111 by a string of 6 A's (which means that we add 1 to the current digit) and $2 G$ 's (which means go to the next digit). Then for example 324 can be obtained from 111 by the string AAGAGAAA. There are in total\n\n$$\n\\frac{8!}{6!\\cdot 2!}=28\n$$\n\nsuch words, so $S$ contains 28 numbers. Now, from the conditions (3), (4), (5), if $\\overline{a b c}$ is in $T$ then each of the other numbers of the form $\\overline{* c}$ cannot be in $T$, neither $\\overline{* *}$ can be, nor $\\overline{a * *}$. Since there are $a+b-2$ numbers of the first category, $a+c-2$ from the second and $b+c-2$ from the third one. In these three categories there are\n\n$$\n(a+b-2)+(b+c-2)+(c+a-2)=2(a+b+c)-6=2 \\cdot 9-6=12\n$$\n\ndistinct numbers that cannot be in $T$ if $\\overline{a b c}$ is in $T$. So, if $T$ has $n$ numbers, then $12 n$ are the forbidden ones that are in $S$, but each number from $S$ can be a forbidden number no more than three times, once for each of its digits, so\n\n$$\nn+\\frac{12 n}{3} \\leq 28 \\Longleftrightarrow n \\leq \\frac{28}{5}\n$$\n\nand since $n$ is an integer, we get $n \\leq 5$. A possible example for $n=5$ is\n\n$$\nT=\\{144,252,315,423,531\\}\n$$\n\nComment by PSC. It is classical to compute the cardinality of $S$ and this can be done in many ways. In general, the number of solutions of the equation\n\n$$\nx_{1}+x_{2}+\\cdots+x_{k}=n\n$$\n\nin positive integers, where the order of $x_{i}$ matters, is well known that equals to $\\binom{n-1}{k-1}$. In our case, we want to count the number of positive solutions to $a+b+c=9$. By the above, this equals to $\\binom{9-1}{3-1}=28$. Using the general result above, we can also find that there are $a+b-2$ numbers of the form $\\overline{* c}$.\n"},"answer":{"kind":"string","value":"5"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":8,"cells":{"problem":{"kind":"string","value":"\nProblem 4. Let $A B C$ be an acute triangle, $A^{\\prime}, B^{\\prime}$ and $C^{\\prime}$ be the reflections of the vertices $A, B$ and $C$ with respect to $B C, C A$, and $A B$, respectively, and let the circumcircles of triangles $A B B^{\\prime}$ and $A C C^{\\prime}$ meet again at $A_{1}$. Points $B_{1}$ and $C_{1}$ are defined similarly. Prove that the lines $A A_{1}, B B_{1}$ and $C C_{1}$ have a common point.\n"},"solution":{"kind":"string","value":"\nSolution. Let $O_{1}, O_{2}$ and $O$ be the circumcenters of triangles $A B B^{\\prime}, A C C^{\\prime}$ and $A B C$ respectively. As $A B$ is the perpendicular bisector of the line segment $C C^{\\prime}, O_{2}$ is the intersection of the perpendicular bisector of $A C$ with $A B$. Similarly, $O_{1}$ is the intersection of the perpendicular bisector of $A B$ with $A C$. It follows that $O$ is the orthocenter of triangle $A O_{1} O_{2}$. This means that $A O$ is perpendicular to $O_{1} O_{2}$. On the other hand, the segment $A A_{1}$ is the common chord of the two circles, thus it is perpendicular to $O_{1} O_{2}$. As a result, $A A_{1}$ passes through $O$. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent at $O$.\n\n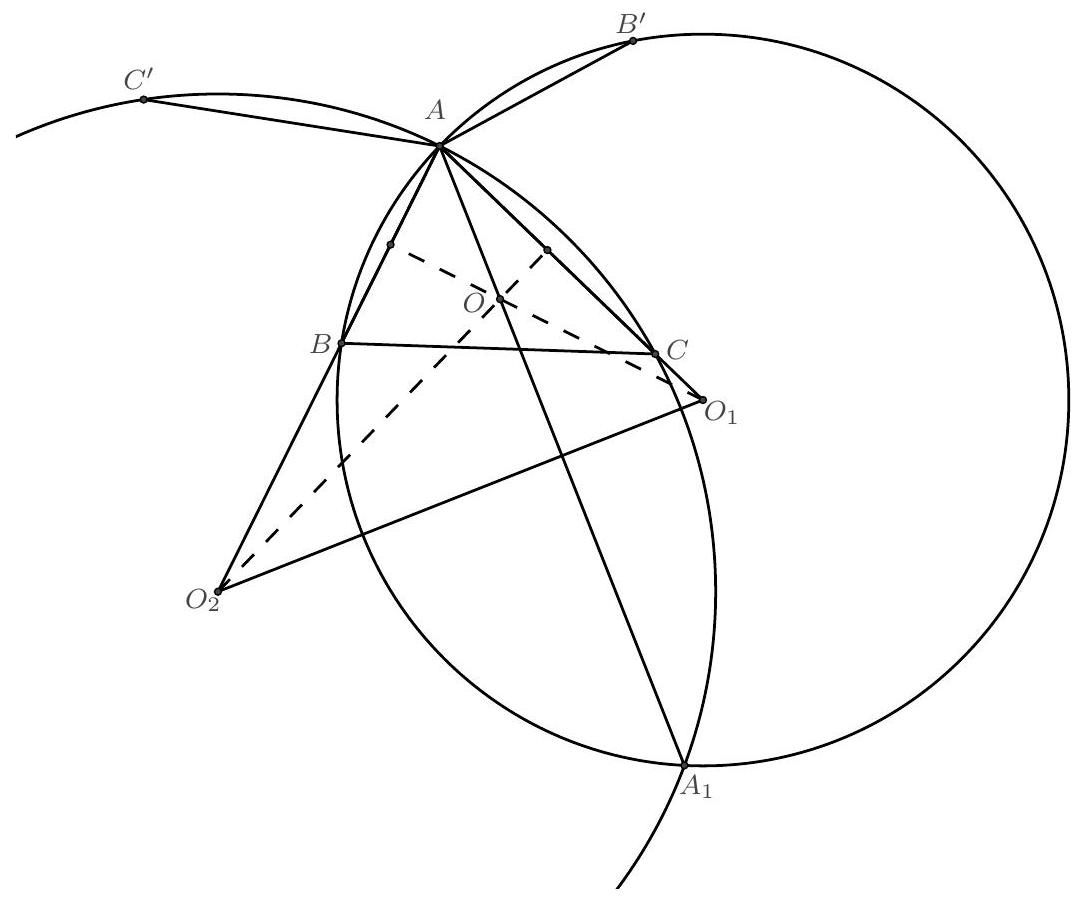![](https://cdn.mathpix.com/cropped/2024_06_05_9020024f2910a9287423g-4.jpg?height=897&width=1087&top_left_y=820&top_left_x=497)\n\nComment by PSC. We present here a different approach.\n\nWe first prove that $A_{1}, B$ and $C^{\\prime}$ are collinear. Indeed, since $\\angle B A B^{\\prime}=\\angle C A C^{\\prime}=2 \\angle B A C$, then from the circles $\\left(A B B^{\\prime}\\right),\\left(A C C^{\\prime}\\right)$ we get\n\n$$\n\\angle A A_{1} B=\\frac{\\angle B A_{1} B^{\\prime}}{2}=\\frac{180^{\\circ}-\\angle B A B^{\\prime}}{2}=90^{\\circ}-\\angle B A C=\\angle A A_{1} C^{\\prime}\n$$\n\nIt follows that\n\n$$\n\\angle A_{1} A C=\\angle A_{1} C^{\\prime} C=\\angle B C^{\\prime} C=90^{\\circ}-\\angle A B C\n$$\n\nOn the other hand, if $O$ is the circumcenter of $A B C$, then\n\n$$\n\\angle O A C=90^{\\circ}-\\angle A B C \\text {. }\n$$\n\nFrom (1) and (2) we conclude that $A_{1}, A$ and $O$ are collinear. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent in $O$.\n\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":9,"cells":{"problem":{"kind":"string","value":"# Problem 1 \n\nLet $a, b$ and $c$ be positive real numbers such that $a+b+c=1$. Prove that\n\n$$\n\\frac{a}{b}+\\frac{b}{a}+\\frac{b}{c}+\\frac{c}{b}+\\frac{c}{a}+\\frac{a}{c}+6 \\geq 2 \\sqrt{2}\\left(\\sqrt{\\frac{1-a}{a}}+\\sqrt{\\frac{1-b}{b}}+\\sqrt{\\frac{1-c}{c}}\\right)\n$$\n\nWhen does equality hold?\n\n"},"solution":{"kind":"string","value":"## Solution\n\nReplacing $1-a, 1-b, 1-c$ with $b+c, c+a, a+b$ respectively on the right hand side, the given inequality becomes\n\n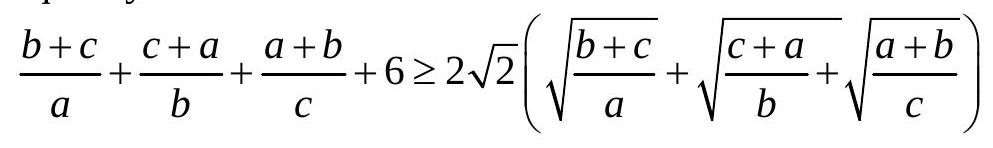![](https://cdn.mathpix.com/cropped/2024_06_05_0ffcf6c39e8d83d98455g-1.jpg?height=148&width=993&top_left_y=1268&top_left_x=497)\n\nand equivalently\n\n$$\n\\left(\\frac{b+c}{a}-2 \\sqrt{2} \\sqrt{\\frac{b+c}{a}}+2\\right)+\\left(\\frac{c+a}{b}-2 \\sqrt{2} \\sqrt{\\frac{c+a}{b}}+2\\right)+\\left(\\frac{a+b}{c}-2 \\sqrt{2} \\sqrt{\\frac{a+b}{c}}+2\\right) \\geq 0\n$$\n\nwhich can be written as\n\n$$\n\\left(\\sqrt{\\frac{b+c}{a}}-\\sqrt{2}\\right)^{2}+\\left(\\sqrt{\\frac{c+a}{b}}-\\sqrt{2}\\right)^{2}+\\left(\\sqrt{\\frac{a+b}{c}}-\\sqrt{2}\\right)^{2} \\geq 0\n$$\n\nwhich is true.\n\nThe equality holds if and only if\n\n$$\n\\frac{b+c}{a}=\\frac{c+a}{b}=\\frac{a+b}{c}\n$$\n\nwhich together with the given condition $a+b+c=1$ gives $a=b=c=\\frac{1}{3}$.\n\n"},"answer":{"kind":"string","value":"=b==\\frac{1}{3}"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":10,"cells":{"problem":{"kind":"string","value":"## Problem 2\n\nLet the circles $k_{1}$ and $k_{2}$ intersect at two distinct points $A$ and $B$, and let $t$ be a common tangent of $k_{1}$ and $k_{2}$, that touches $k_{1}$ and $k_{2}$ at $M$ and $N$, respectively. If $t \\perp A M$ and $M N=2 A M$, evaluate $\\angle N M B$.\n\n"},"solution":{"kind":"string","value":"## Solution 1\n\nLet $P$ be the symmetric of $A$ with respect to $M$ (Figure 1). Then $A M=M P$ and $t \\perp A P$, hence the triangle $A P N$ is isosceles with $A P$ as its base, so $\\angle N A P=\\angle N P A$. We have $\\angle B A P=\\angle B A M=\\angle B M N$ and $\\angle B A N=\\angle B N M$.\n\nThus we have\n\n$$\n180^{\\circ}-\\angle N B M=\\angle B N M+\\angle B M N=\\angle B A N+\\angle B A P=\\angle N A P=\\angle N P A\n$$\n\nso the quadrangle $M B N P$ is cyclic (since the points $B$ and $P$ lie on different sides of $M N$ ). Hence $\\angle A P B=\\angle M P B=\\angle M N B$ and the triangles $A P B$ and $M N B$ are congruent ( $M N=2 A M=A M+M P=A P$ ). From that we get $A B=M B$, i.e. the triangle $A M B$ is isosceles, and since $t$ is tangent to $k_{1}$ and perpendicular to $A M$, the centre of $k_{1}$ is on $A M$, hence $A M B$ is a right-angled triangle. From the last two statements we infer $\\angle A M B=45^{\\circ}$, and so $\\angle N M B=90^{\\circ}-\\angle A M B=45^{\\circ}$.\n\n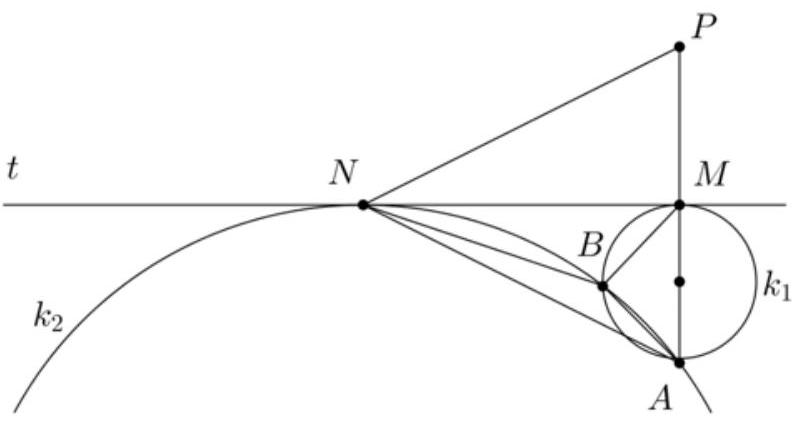![](https://cdn.mathpix.com/cropped/2024_06_05_0ffcf6c39e8d83d98455g-2.jpg?height=423&width=809&top_left_y=1162&top_left_x=632)\n\nFigure 1\n\n"},"answer":{"kind":"string","value":"45"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":11,"cells":{"problem":{"kind":"string","value":"## Problem 3\n\nOn a board there are $n$ nails each two connected by a string. Each string is colored in one of $n$ given distinct colors. For each three distinct colors, there exist three nails connected with strings in these three colors. Can $n$ be\na) 6 ?\nb) 7 ?\n"},"solution":{"kind":"string","value":"\nSolution. (a) The answer is no.\n\nSuppose it is possible. Consider some color, say blue. Each blue string is the side of 4 triangles formed with vertices on the given points. As there exist $\\binom{5}{2}=\\frac{5 \\cdot 4}{2}=10$ pairs of colors other than blue, and for any such pair of colors together with the blue color there exists a triangle with strings in these colors, we conclude that there exist at least 3 blue strings (otherwise the number of triangles with a blue string as a side would be at most $2 \\cdot 4=8$, a contradiction). The same is true for any color, so altogether there exist at least $6 \\cdot 3=18$ strings, while we have just $\\binom{6}{2}=\\frac{6 \\cdot 5}{2}=15$ of them.\n\n(b) The answer is yes\n\nPut the nails at the vertices of a regular 7-gon and color each one of its sides in a different color. Now color each diagonal in the color of the unique side parallel to it. It can be checked directly that each triple of colors appears in some triangle (because of symmetry, it is enough to check only the triples containing the first color).\n\n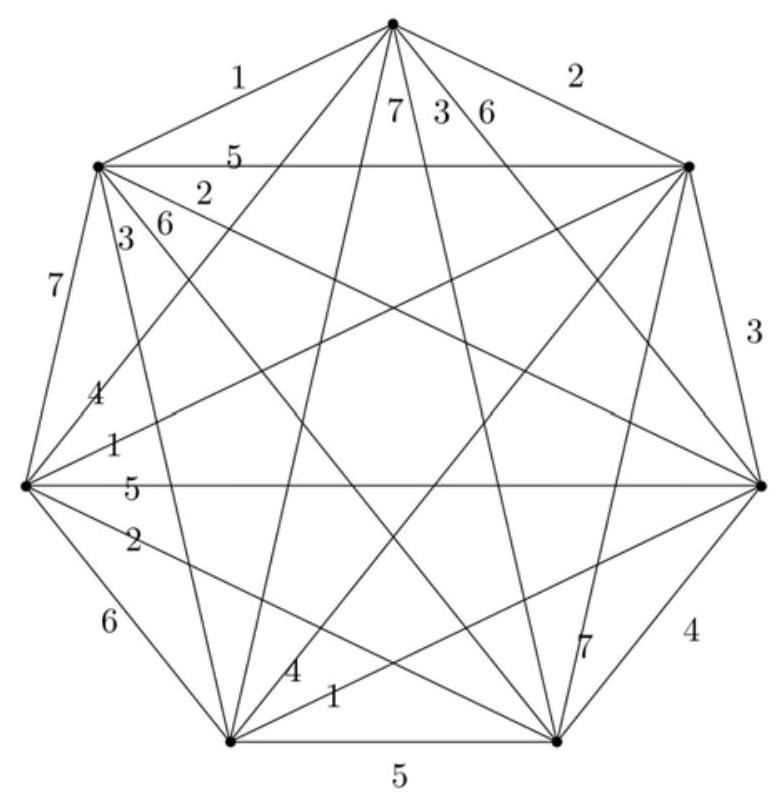![](https://cdn.mathpix.com/cropped/2024_06_05_0ffcf6c39e8d83d98455g-3.jpg?height=794&width=780&top_left_y=1322&top_left_x=638)\n\nRemark. The argument in (a) can be applied to any even n. The argument in (b) can be applied to any odd $n=2 k+1$ as follows: first number the nails as $0,1,2 \\ldots, 2 k$ and similarly number the colors as $0,1,2 \\ldots, 2 k$. Then connect nail $x$ with nail $y$ by a string of color $x+y(\\bmod n)$. For each triple of colors $(p, q, r)$ there are vertices $x, y, z$ connected by these three colors. Indeed, we need to solve $(\\bmod n)$ the system\n\n$$\n(*)(x+y \\equiv p, x+z \\equiv q, y+z \\equiv r)\n$$\n\nAdding all three, we get $2(x+y+z) \\equiv p+q+r$ and multiplying by $k+1$ we get $x+y+z \\equiv(k+1)(p+q+r)$. We can now find $x, y, z$ from the identities $(*)$.\n\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":12,"cells":{"problem":{"kind":"string","value":"## Problem 4\n\nFind all positive integers $x, y, z$ and $t$ such that\n\n$$\n2^{x} \\cdot 3^{y}+5^{z}=7^{t}\n$$\n\n"},"solution":{"kind":"string","value":"## Solution\n\nReducing modulo 3 we get $5^{z} \\equiv 1$, therefore $z$ is even, $z=2 c, c \\in \\mathbb{N}$.\n\nNext we prove that $t$ is even:\n\nObviously, $t \\geq 2$. Let us suppose that $t$ is odd, say $t=2 d+1, d \\in \\mathbb{N}$. The equation becomes $2^{x} \\cdot 3^{y}+25^{c}=7 \\cdot 49^{d}$. If $x \\geq 2$, reducing modulo 4 we get $1 \\equiv 3$, a contradiction. And if $x=1$, we have $2 \\cdot 3^{y}+25^{c}=7 \\cdot 49^{d}$ and reducing modulo 24 we obtain\n\n$$\n2 \\cdot 3^{y}+1 \\equiv 7 \\Rightarrow 24 \\mid 2\\left(3^{y}-3\\right) \\text {, i.e. } 4 \\mid 3^{y-1}-1\n$$\n\nwhich means that $y-1$ is even. Then $y=2 b+1, b \\in \\mathbb{N}$. We obtain $6 \\cdot 9^{b}+25^{c}=7 \\cdot 49^{d}$, and reducing modulo 5 we get $(-1)^{b} \\equiv 2 \\cdot(-1)^{d}$, which is false for all $b, d \\in \\mathbb{N}$. Hence $t$ is even, $t=2 d, d \\in \\mathbb{N}$, as claimed.\n\nNow the equation can be written as\n\n$$\n2^{x} \\cdot 3^{y}+25^{d}=49^{d} \\Leftrightarrow 2^{x} \\cdot 3^{y}=\\left(7^{d}-5^{c}\\right)\\left(7^{d}+5^{c}\\right)\n$$\n\nAs $\\operatorname{gcd}\\left(7^{d}-5^{c}, 7^{d}+5^{c}\\right)=2$ and $7^{d}+5^{c}>2$, there exist exactly three possibilities:\n(1) $\\left\\{\\begin{array}{l}7^{\\mathrm{d}}-5^{\\mathrm{d}}=2^{\\mathrm{x-1}} \\\\ 7^{\\mathrm{d}}+5^{\\mathrm{d}}=2 \\cdot 3^{y}\\end{array} ;\\right.$\n(2) $\\left\\{\\begin{array}{l}7^{\\mathrm{d}}-5^{\\mathrm{d}}=2 \\cdot 3^{\\mathrm{y}} \\\\ 7^{\\mathrm{d}}+5^{\\mathrm{d}}=2^{\\mathrm{x-1}}\\end{array}\\right.$;\n(3) $\\left\\{\\begin{array}{l}7^{d}-5^{d}=2 \\\\ 7^{d}+5^{d}=2^{x-1} \\cdot 3^{y}\\end{array}\\right.$\n\n## Case (1)\n\nWe have $7^{d}=2^{x-2}+3^{y}$ and reducing modulo 3 , we get $2^{x-2} \\equiv 1(\\bmod 3)$, hence $x-2$ is even, i.e. $x=2 a+2, a \\in \\mathbb{N}$, where $a>0$, since $a=0$ would mean $3^{y}+1=7^{d}$, which is impossible (even $=$ odd).\n\nWe obtain\n\n$$\n7^{d}-5^{d}=2 \\cdot 4^{a} \\stackrel{\\bmod 4}{\\Rightarrow} 7^{d} \\equiv 1(\\bmod 4) \\Rightarrow d=2 e, e \\in \\mathbb{N}\n$$\n\nThen we have\n\n$$\n49^{e}-5^{d}=2 \\cdot 4^{a} \\stackrel{\\bmod 8}{\\Rightarrow} 5^{c} \\equiv 1(\\bmod 8) \\Rightarrow c=2 f, f \\in \\mathbb{N}\n$$\n\nWe obtain $49^{e}-25^{f}=2 \\cdot 4^{a} \\stackrel{\\text { mod } 3}{\\Rightarrow} 0 \\equiv 2(\\bmod 3)$, false. In conclusion, in this case there are no solutions to the equation.\n\n## Case (2)\n\nFrom $2^{x-1}=7^{d}+5^{c} \\geq 12$ we obtain $x \\geq 5$. Then $7^{d}+5^{c} \\equiv 0(\\bmod 4)$, i.e. $3^{d}+1 \\equiv 0(\\bmod 4)$, hence $d$ is odd. As $7^{d}=5^{c}+2 \\cdot 3^{y} \\geq 11$, we get $d \\geq 2$, hence $d=2 e+1, e \\in \\mathbb{N}$.\n\nAs in the previous case, from $7^{d}=2^{x-2}+3^{y}$ reducing modulo 3 we obtain $x=2 a+2$ with $a \\geq 2$ (because $x \\geq 5$ ). We get $7^{d}=4^{a}+3^{y}$ i.e. $7 \\cdot 49^{e}=4^{a}+3^{y}$, hence, reducing modulo 8 we obtain $7 \\equiv 3^{y}$ which is false, because $3^{y}$ is congruent either to 1 (if $y$ is even) or to 3 (if $y$ is odd). In conclusion, in this case there are no solutions to the equation.\n\n## Case (3)\n\nFrom $7^{d}=5^{c}+2$ it follows that the last digit of $7^{d}$ is 7 , hence $d=4 k+1, k \\in \\mathbb{N}$.\n\nIf $c \\geq 2$, from $7^{4 k+1}=5^{c}+2$ reducing modulo 25 we obtain $7 \\equiv 2(\\bmod 25)$ which is false. For $c=1$ we get $d=1$ and the solution $x=3, y=1, z=t=2$.\n\n"},"answer":{"kind":"string","value":"3,1,=2"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":13,"cells":{"problem":{"kind":"string","value":"\nProblem 1. The real numbers $a, b, c, d$ satisfy simultaneously the equations\n\n$$\na b c-d=1, b c d-a=2, c d a-b=3, d a b-c=-6\n$$\n\nProve that $a+b+c+d \\neq 0$.\n"},"solution":{"kind":"string","value":"\nSolution. Suppose that $a+b+c+d=0$. Then\n\n$$\na b c+b c d+c d a+d a b=0\n$$\n\nIf $a b c d=0$, then one of numbers, say $d$, must be 0 . In this case $a b c=0$, and so at least two of the numbers $a, b, c, d$ will be equal to 0 , making one of the given equations impossible. Hence $a b c d \\neq 0$ and, from (1),\n\n$$\n\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}+\\frac{1}{d}=0\n$$\n\nimplying\n\n$$\n\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}=\\frac{1}{a+b+c}\n$$\n\nIt follows that $(a+b)(b+c)(c+a)=0$, which is impossible (for instance, if $a+b=0$, then adding the second and third given equations would lead to $0=2+3$, a contradiction). Thus $a+b+c+d \\neq 0$.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Algebra"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":14,"cells":{"problem":{"kind":"string","value":"\nProblem 3. Let $A L$ and $B K$ be angle bisectors in the non-isosceles triangle $A B C$ ( $L$ lies on the side $B C, K$ lies on the side $A C$ ). The perpendicular bisector of $B K$ intersects the line $A L$ at point $M$. Point $N$ lies on the line $B K$ such that $L N$ is parallel to $M K$. Prove that $L N=N A$.\n"},"solution":{"kind":"string","value":"\nSolution. The point $M$ lies on the circumcircle of $\\triangle A B K$ (since both $A L$ and the perpendicular bisector of $B K$ bisect the arc $B K$ of this circle). Then $\\angle C B K=$ $\\angle A B K=\\angle A M K=\\angle N L A$. Thus $A B L N$ is cyclic, whence $\\angle N A L=\\angle N B L=$ $\\angle C B K=\\angle N L A$. Now it follows that $L N=N A$.\n\n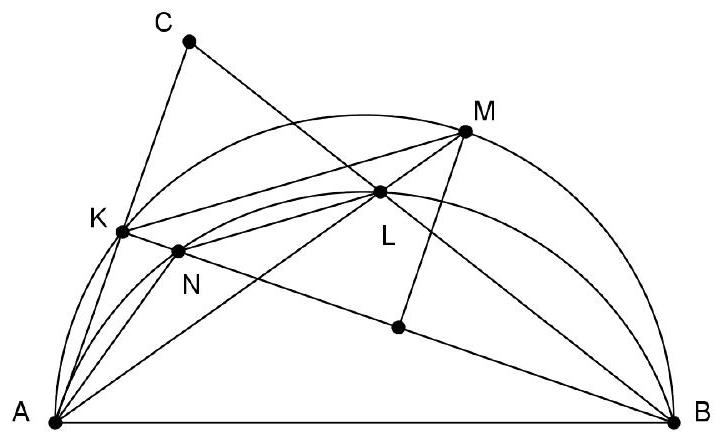![](https://cdn.mathpix.com/cropped/2024_06_05_3a1fd0d6eb71bd45a2e0g-2.jpg?height=440&width=719&top_left_y=400&top_left_x=677)\n"},"answer":{"kind":"string","value":"LN=NA"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":15,"cells":{"problem":{"kind":"string","value":"\nProblem 4. A $9 \\times 7$ rectangle is tiled with tiles of the two types shown in the picture below (the tiles are composed by three, respectively four unit squares and the L-shaped tiles can be rotated repeatedly with $90^{\\circ}$ ).\n![](https://cdn.mathpix.com/cropped/2024_06_05_3a1fd0d6eb71bd45a2e0g-2.jpg?height=130&width=506&top_left_y=1094&top_left_x=776)\n\nLet $n \\geqslant 0$ be the number of the $2 \\times 2$ tiles which can be used in such a tiling. Find all the values of $n$.\n"},"solution":{"kind":"string","value":"\nSolution. Answer: 0 or 3 .\n\nDenote by $x$ the number of the pieces of the type ornerănd by $y$ the number of the pieces of the type of $2 \\times 2$. Mark 20 squares of the rectangle as in the figure below.\n\n![](https://cdn.mathpix.com/cropped/2024_06_05_3a1fd0d6eb71bd45a2e0g-2.jpg?height=300&width=389&top_left_y=1549&top_left_x=842)\n\nObviously, each piece covers at most one marked square.\n\nThus, $x+y \\geq 20$ (1) and consequently $3 x+3 y \\geq 60(2)$. On the other hand $3 x+4 y=63$ (3). From (2) and (3) it follows $y \\leq 3$ and from (3), $3 \\mid y$.\n\nThe proof is finished if we produce tilings with 3 , respectively $0,2 \\times 2$ tiles:\n![](https://cdn.mathpix.com/cropped/2024_06_05_3a1fd0d6eb71bd45a2e0g-2.jpg?height=306&width=834&top_left_y=2130&top_left_x=614)\n\n"},"answer":{"kind":"string","value":"0or3"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Incomplete"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":16,"cells":{"problem":{"kind":"string","value":"\nProblem 1. Let $n(n \\geq 1)$ be an integer. Consider the equation\n\n$$\n2 \\cdot\\left\\lfloor\\frac{1}{2 x}\\right\\rfloor-n+1=(n+1)(1-n x)\n$$\n\nwhere $x$ is the unknown real variable.\n\n(a) Solve the equation for $n=8$.\n\n(b) Prove that there exists an integer $n$ for which the equation has at least 2021 solutions. (For any real number $y$ by $\\lfloor y\\rfloor$ we denote the largest integer $m$ such that $m \\leq y$.)\n"},"solution":{"kind":"string","value":"\nSolution. Let $k=\\left[\\frac{1}{2 x}\\right], k \\in \\mathbb{Z}$.\n\n(a) For $n=8$, the equation becomes\n\n$$\nk=\\left[\\frac{1}{2 x}\\right]=8-36 x \\Rightarrow x \\neq 0 \\text { and } x=\\frac{8-k}{36}\n$$\n\nSince $x \\neq 0$, we have $k \\neq 8$, and the last relation implies $k=\\left[\\frac{1}{2 x}\\right]=\\left[\\frac{18}{8-k}\\right]$. Checking signs, we see that $02021$ ensures that there exist at least 2021 integer values of $k$ which satisfy (2).\n"},"answer":{"kind":"string","value":""},"problem_type":{"kind":"string","value":"Algebra"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":17,"cells":{"problem":{"kind":"string","value":"\nProblem 2. For any set $A=\\left\\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\\right\\}$ of five distinct positive integers denote by $S_{A}$ the sum of its elements, and denote by $T_{A}$ the number of triples $(i, j, k)$ with $1 \\leqslant i<j<k \\leqslant 5$ for which $x_{i}+x_{j}+x_{k}$ divides $S_{A}$.\n\nFind the largest possible value of $T_{A}$.\n"},"solution":{"kind":"string","value":"\nSolution. We will prove that the maximum value that $T_{A}$ can attain is 4 . Let $A=$ $\\left\\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\\right\\}$ be a set of five positive integers such that $x_{1}x_{4}$ and $x_{3}>x_{2}$. Analogously we can show that any triple of form $(x, y, 5)$ where $y>2$ isn't good.\n\nBy above, the number of good triples can be at most 5 and only triples $(1,2,5),(2,3,4)$, $(1,3,4),(1,2,4),(1,2,3)$ can be good. But if triples $(1,2,5)$ and $(2,3,4)$ are simultaneously good we have that:\n\n$$\nx_{1}+x_{2}+x_{5} \\mid x_{3}+x_{4} \\Rightarrow x_{5}<x_{3}+x_{4}\n$$\n\nand\n\n$$\nx_{2}+x_{3}+x_{4} \\mid x_{1}+x_{5} \\Rightarrow x_{2}+x_{3}+x_{4} \\leqslant x_{1}+x_{5} \\stackrel{(1)}{<} x_{1}+x_{3}+x_{4}<x_{2}+x_{3}+x_{4},\n$$\n\nwhich is impossible. Therefore, $T_{A} \\leqslant 4$.\n\nAlternatively, one can prove the statement above by adding up the two inequalities $x_{1}+x_{2}+x_{4}<x_{3}+x_{4}$ and $x_{2}+x_{3}+x_{4}<x_{1}+x_{5}$ that are derived from the divisibilities.\n\nTo show that $T_{A}=4$ is possible, consider the numbers $1,2,3,4,494$. This works because $6|498,7| 497,8 \\mid 496$, and $9 \\mid 495$.\n\nRemark. The motivation for construction is to realize that if we choose $x_{1}, x_{2}, x_{3}, x_{4}$ we can get all the conditions $x_{5}$ must satisfy. Let $S=x_{1}+x_{2}+x_{3}+x_{4}$. Now we have to choose $x_{5}$ such that\n\n$$\nS-x_{i} \\mid x_{i}+x_{5} \\text {, i.e. } x_{5} \\equiv-x_{i} \\quad \\bmod \\left(S-x_{i}\\right) \\forall i \\in\\{1,2,3,4\\}\n$$\n\nBy the Chinese Remainder Theorem it is obvious that if $S-x_{1}, S-x_{2}, S-x_{3}, S-x_{4}$ are pairwise coprime, such $x_{5}$ must exist. To make all these numbers pairwise coprime it's natural to take $x_{1}, x_{2}, x_{3}, x_{4}$ to be all odd and then solve mod 3 issues. Fortunately it can be seen that $1,5,7,11$ easily works because $13,17,19,23$ are pairwise coprime.\n\nHowever, even without the knowledge of this theorem it makes sense intuitively that this system must have a solution for some $x_{1}, x_{2}, x_{3}, x_{4}$. By taking $\\left(x_{1}, x_{2}, x_{3}, x_{4}\\right)=$ $(1,2,3,4)$ we get pretty simple system which can be solved by hand rather easily.\n"},"answer":{"kind":"string","value":"4"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":18,"cells":{"problem":{"kind":"string","value":"\nProblem 3. Let $A B C$ be an acute scalene triangle with circumcenter $O$. Let $D$ be the foot of the altitude from $A$ to the side $B C$. The lines $B C$ and $A O$ intersect at $E$. Let $s$ be the line through $E$ perpendicular to $A O$. The line $s$ intersects $A B$ and $A C$ at $K$ and $L$, respectively. Denote by $\\omega$ the circumcircle of triangle $A K L$. Line $A D$ intersects $\\omega$ again at $X$.\n\nProve that $\\omega$ and the circumcircles of triangles $A B C$ and $D E X$ have a common point.\n\n"},"solution":{"kind":"string","value":"## Solution.\n\n![](https://cdn.mathpix.com/cropped/2024_06_05_59a54a44649abed37d52g-3.jpg?height=821&width=853&top_left_y=798&top_left_x=598)\n\nLet us denote angles of triangle $A B C$ with $\\alpha, \\beta, \\gamma$ in a standard way. By basic anglechasing we have\n\n$$\n\\angle B A D=90^{\\circ}-\\beta=\\angle O A C \\text { and } \\angle C A D=\\angle B A O=90^{\\circ}-\\gamma\n$$\n\nUsing the fact that lines $A E$ and $A X$ are isogonal with respect to $\\angle K A L$ we can conclude that $X$ is an $A$-antipode on $\\omega$. (This fact can be purely angle-chased: we have\n\n$$\n\\angle K A X+\\angle A X K=\\angle K A X+\\angle A L K=90^{\\circ}-\\beta+\\beta=90^{\\circ}\n$$\n\nwhich implies $\\angle A K X=90^{\\circ}$ ). Now let $F$ be the projection of $X$ on the line $A E$. Using that $A X$ is a diameter of $\\omega$ and $\\angle E D X=90^{\\circ}$ it's clear that $F$ is the intersection point of $\\omega$ and the circumcircle of triangle $D E X$. Now it suffices to show that $A B F C$ is cyclic. We have $\\angle K L F=\\angle K A F=90^{\\circ}-\\gamma$ and from $\\angle F E L=90^{\\circ}$ we have that $\\angle E F L=\\gamma=\\angle E C L$ so quadrilateral $E F C L$ is cyclic. Next, we have\n\n$$\n\\angle A F C=\\angle E F C=180^{\\circ}-\\angle E L C=\\angle E L A=\\beta\n$$\n\n(where last equality holds because of $\\angle A E L=90^{\\circ}$ and $\\angle E A L=90^{\\circ}-\\beta$ ).\n\n![](https://cdn.mathpix.com/cropped/2024_06_05_59a54a44649abed37d52g-4.jpg?height=834&width=857&top_left_y=369&top_left_x=596)\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":19,"cells":{"problem":{"kind":"string","value":"\nProblem 4. Let $M$ be a subset of the set of 2021 integers $\\{1,2,3, \\ldots, 2021\\}$ such that for any three elements (not necessarily distinct) $a, b, c$ of $M$ we have $|a+b-c|>10$. Determine the largest possible number of elements of $M$.\n"},"solution":{"kind":"string","value":"\nSolution. The set $M=\\{1016,1017, \\ldots, 2021\\}$ has 1006 elements and satisfies the required property, since $a, b, c \\in M$ implies that $a+b-c \\geqslant 1016+1016-2021=11$. We will show that this is optimal.\n\nSuppose $M$ satisfies the condition in the problem. Let $k$ be the minimal element of $M$. Then $k=|k+k-k|>10 \\Rightarrow k \\geqslant 11$. Note also that for every $m$, the integers $m, m+k-10$ cannot both belong to $M$, since $k+m-(m+k-10)=10$.\n\nClaim 1: $M$ contains at most $k-10$ out of any $2 k-20$ consecutive integers.\n\nProof: We can partition the set $\\{m, m+1, \\ldots, m+2 k-21\\}$ into $k-10$ pairs as follows:\n\n$$\n\\{m, m+k-10\\},\\{m+1, m+k-9\\}, \\ldots,\\{m+k-11, m+2 k-21\\}\n$$\n\nIt remains to note that $M$ can contain at most one element of each pair.\n\nClaim 2: $M$ contains at most $[(t+k-10) / 2]$ out of any $t$ consecutive integers.\n\nProof: Write $t=q(2 k-20)+r$ with $r \\in\\{0,1,2 \\ldots, 2 k-21\\}$. From the set of the first $q(2 k-20)$ integers, by Claim 1 at most $q(k-10)$ can belong to $M$. Also by claim 1, it follows that from the last $r$ integers, at $\\operatorname{most} \\min \\{r, k-10\\}$ can belong to $M$.\n\nThus,\n\n- If $r \\leqslant k-10$, then at most\n\n$$\nq(k-10)+r=\\frac{t+r}{2} \\leqslant \\frac{t+k-10}{2} \\text { integers belong to } M\n$$\n\n- If $r>k-10$, then at most\n\n$$\nq(k-10)+k-10=\\frac{t-r+2(k-10)}{2} \\leqslant \\frac{t+k-10}{2} \\text { integers belong to } M\n$$\n\nBy Claim 2, the number of elements of $M$ amongst $k+1, k+2, \\ldots, 2021$ is at most\n\n$$\n\\left[\\frac{(2021-k)+(k-10)}{2}\\right]=1005\n$$\n\nSince amongst $\\{1,2, \\ldots, k\\}$ only $k$ belongs to $M$, we conclude that $M$ has at most 1006 elements as claimed.\n\n"},"answer":{"kind":"string","value":"1006"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":20,"cells":{"problem":{"kind":"string","value":"\nProblem 1. Find all distinct prime numbers $p, q$ and $r$ such that\n\n$$\n3 p^{4}-5 q^{4}-4 r^{2}=26\n$$\n"},"solution":{"kind":"string","value":"\nSolution. First notice that if both primes $q$ and $r$ differ from 3 , then $q^{2} \\equiv r^{2} \\equiv 1(\\bmod 3)$, hence the left hand side of the given equation is congruent to zero modulo 3 , which is impossible since 26 is not divisible by 3 . Thus, $q=3$ or $r=3$. We consider two cases.\n\nCase 1. $q=3$.\n\nThe equation reduces to $3 p^{4}-4 r^{2}=431$\n\nIf $p \\neq 5, \\quad$ by Fermat's little theorem, $\\quad p^{4} \\equiv 1(\\bmod 5)$, which yields $3-4 r^{2} \\equiv 1(\\bmod 5), \\quad$ or equivalently, $\\quad r^{2}+2 \\equiv 0(\\bmod 5)$. The last congruence is impossible in view of the fact that a residue of a square of a positive integer belongs to the set $\\{0,1,4\\}$. Therefore $p=5$ and $r=19$.\n\nCase 2. $r=3$.\n\nThe equation becomes $3 p^{4}-5 q^{4}=62$\n\nObviously $p \\neq 5$. Hence, Fermat's little theorem gives $p^{4} \\equiv 1(\\bmod 5)$. But then $5 q^{4} \\equiv 1(\\bmod 5)$, which is impossible .\n\nHence, the only solution of the given equation is $p=5, q=3, r=19$.\n"},"answer":{"kind":"string","value":"p=5,q=3,r=19"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":21,"cells":{"problem":{"kind":"string","value":"\nProblem 2. Consider an acute triangle $A B C$ with area S. Let $C D \\perp A B \\quad(D \\in A B)$, $D M \\perp A C \\quad(M \\in A C)$ and $\\quad D N \\perp B C \\quad(N \\in B C)$. Denote by $H_{1}$ and $H_{2}$ the orthocentres of the triangles $M N C$ and $M N D$ respectively. Find the area of the quadrilateral $\\mathrm{AH}_{1} \\mathrm{BH}_{2}$ in terms of $S$.\n"},"solution":{"kind":"string","value":"\nSolution 1. Let $O, P, K, R$ and $T$ be the mid-points of the segments $C D, M N$, $C N, C H_{1}$ and $M H_{1}$, respectively. From $\\triangle M N C$ we have that $\\overline{P K}=\\frac{1}{2} \\overline{M C}$ and $P K \\| M C$. Analogously, from $\\Delta M H_{1} C$ we have that $\\overline{T R}=\\frac{1}{2} \\overline{M C}$ and $T R \\| M C$. Consequently, $\\overline{P K}=\\overline{T R}$ and $P K \\| T R$. Also $O K \\| D N \\quad$ (from\n\n![](https://cdn.mathpix.com/cropped/2024_06_05_e8f9a14accde81c04529g-2.jpg?height=657&width=834&top_left_y=554&top_left_x=994)\n\n$\\triangle C D N$ ) and since $D N \\perp B C$ and $M H_{1} \\perp B C$, it follows that $T H_{1} \\| O K$. Since $O$ is the circumcenter of $\\triangle C M N, O P \\perp M N$. Thus, $C H_{1} \\perp M N$ implies $O P \\| C H_{1}$. We conclude $\\triangle T R H_{1} \\cong \\triangle K P O \\quad$ (they have parallel sides and $\\overline{T R}=\\overline{P K}$ ), hence $\\overline{R H_{1}}=\\overline{P O}$, i.e. $\\overline{C H_{1}}=2 \\overline{P O}$ and $C H_{1} \\| P O$.\n\nAnalogously, $\\overline{D H_{2}}=2 \\overline{P O} \\quad$ and $\\quad D H_{2} \\| P O$. From $\\quad \\overline{C H_{1}}=2 \\overline{P O}=\\overline{D H_{2}} \\quad$ and $C H_{1}\\|P O\\| D H_{2}$ the quadrilateral $C H_{1} H_{2} D$ is a parallelogram, thus $\\overline{H_{1} H_{2}}=\\overline{C D}$ and $H_{1} H_{2} \\| C D$. Therefore the area of the quadrilateral $A H_{1} B H_{2}$ is $\\frac{\\overline{A B} \\cdot \\overline{H_{1} H_{2}}}{2}=\\frac{\\overline{A B} \\cdot \\overline{C D}}{2}=S$.\n"},"answer":{"kind":"string","value":"S"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":22,"cells":{"problem":{"kind":"string","value":"\nProblem 3. Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that\n\n$$\n\\left(a+\\frac{1}{b}\\right)^{2}+\\left(b+\\frac{1}{c}\\right)^{2}+\\left(c+\\frac{1}{a}\\right)^{2} \\geq 3(a+b+c+1)\n$$\n\nWhen does equality hold?\n"},"solution":{"kind":"string","value":"\nSolution 1. By using AM-GM $\\left(x^{2}+y^{2}+z^{2} \\geq x y+y z+z x\\right)$ we have\n\n$$\n\\begin{aligned}\n\\left(a+\\frac{1}{b}\\right)^{2}+\\left(b+\\frac{1}{c}\\right)^{2}+\\left(c+\\frac{1}{a}\\right)^{2} & \\geq\\left(a+\\frac{1}{b}\\right)\\left(b+\\frac{1}{c}\\right)+\\left(b+\\frac{1}{c}\\right)\\left(c+\\frac{1}{a}\\right)+\\left(c+\\frac{1}{a}\\right)\\left(a+\\frac{1}{b}\\right) \\\\\n& =\\left(a b+1+\\frac{a}{c}+a\\right)+\\left(b c+1+\\frac{b}{a}+b\\right)+\\left(c a+1+\\frac{c}{b}+c\\right) \\\\\n& =a b+b c+c a+\\frac{a}{c}+\\frac{c}{b}+\\frac{b}{a}+3+a+b+c\n\\end{aligned}\n$$\n\nNotice that by AM-GM we have $a b+\\frac{b}{a} \\geq 2 b, b c+\\frac{c}{b} \\geq 2 c$, and $c a+\\frac{a}{c} \\geq 2 a$.\n\nThus ,\n\n$\\left(a+\\frac{1}{b}\\right)^{2}+\\left(b+\\frac{1}{c}\\right)^{2}+\\left(c+\\frac{1}{a}\\right)^{2} \\geq\\left(a b+\\frac{b}{a}\\right)+\\left(b c+\\frac{c}{b}\\right)+\\left(c a+\\frac{a}{c}\\right)+3+a+b+c \\geq 3(a+b+c+1)$.\n\nThe equality holds if and only if $a=b=c=1$.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":23,"cells":{"problem":{"kind":"string","value":"\nProblem 4. For a positive integer $n$, two players A and B play the following game: Given a pile of $s$ stones, the players take turn alternatively with A going first. On each turn the player is allowed to take either one stone, or a prime number of stones, or a multiple of $n$ stones. The winner is the one who takes the last stone. Assuming both $\\mathrm{A}$ and $\\mathrm{B}$ play perfectly, for how many values of $s$ the player A cannot win?\n"},"solution":{"kind":"string","value":"\nSolution. Denote by $k$ the sought number and let $\\left\\{s_{1}, \\mathrm{~s}_{2}, \\ldots, \\mathrm{s}_{k}\\right\\}$ be the corresponding values for $s$. We call each $s_{i}$ a losing number and every other nonnegative integer a winning numbers.\n\n## Clearly every multiple of $n$ is a winning number.\n\nSuppose there are two different losing numbers $s_{i}>s_{j}$, which are congruent modulo $n$. Then, on his first turn of play, player $A$ may remove $s_{i}-s_{j}$ stones (since $n \\mid s_{i}-s_{j}$ ), leaving a pile with $s_{j}$ stones for B. This is in contradiction with both $s_{i}$ and $s_{j}$ being losing numbers.\n\nHence, there are at most $n-1$ losing numbers, i.e. $k \\leq n-1$.\n\nSuppose there exists an integer $r \\in\\{1,2, \\ldots, n-1\\}$, such that $m n+r$ is a winning number for every $m \\in \\mathbb{N}_{0}$. Let us denote by $u$ the greatest losing number (if $k>0$ ) or 0 (if $k=0)$, and let $s=\\operatorname{LCM}(2,3, \\ldots, u+n+1)$. Note that all the numbers $s+2, s+3, \\ldots$, $s+u+n+1 \\quad$ are composite. Let $m^{\\prime} \\in \\mathbb{N}_{0}$, be such that $s+u+2 \\leq m^{\\prime} n+r \\leq s+u+n+1$. In order for $m^{\\prime} n+r$ to be a winning number, there must exist an integer $p$, which is either one, or prime, or a positive multiple of $n$, such that $m^{\\prime} n+r-p$ is a losing number or 0 , and hence lesser than or equal to $u$. Since $s+2 \\leq m^{\\prime} n+r-u \\leq p \\leq m^{\\prime} n+r \\leq s+u+n+1, p$ must be a composite, hence $p$ is a multiple of $n$ (say $p=q n$ ). But then $m^{\\prime} n+r-p=\\left(m^{\\prime}-q\\right) n+r$ must be a winning number, according to our assumption. This contradicts our assumption that all numbers $m n+r, m \\in \\mathbb{N}_{0}$ are winning.\n\nHence, each nonzero residue class modulo $n$ contains a loosing number.\n\nThere are exactly $n-1$ losing numbers .\n\nLemma: No pair $(u, n)$ of positive integers satisfies the following property:\n\n$(*) \\quad$ In $\\mathbb{N}$ exists an arithmetic progression $\\left(a_{t}\\right)_{t=1}^{\\infty}$ with difference $n$ such that each segment\n\n$\\left[a_{i}-u, a_{i}+u\\right]$ contains a prime.\n\nProof of the lemma: Suppose such a pair $(u, n)$ and a corresponding arithmetic progression $\\left(\\mathrm{a}_{t}\\right)_{t=1}^{\\infty}$ exist. In $\\mathbb{N}$ exist arbitrarily long patches of consecutive composites. Take such a patch $P$ of length $3 u n$. Then, at least one segment $\\left[a_{i}-u, a_{i}+u\\right]$ is fully contained in $P$, a contradiction.\n\nSuppose such a nonzero residue class modulo $n$ exists (hence $n>1$ ). Let $u \\in \\mathbb{N}$ be greater than every loosing number. Consider the members of the supposed residue class which are greater than $u$. They form an arithmetic progression with the property $\\left({ }^{*}\\right)$, a contradiction (by the lemma).\n\n"},"answer":{"kind":"string","value":"n-1"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":24,"cells":{"problem":{"kind":"string","value":"\nProblem 1. Find all pairs $(a, b)$ of positive integers such that\n\n$$\n11 a b \\leq a^{3}-b^{3} \\leq 12 a b\n$$\n"},"solution":{"kind":"string","value":"\nSolution 1. Let $a-b=t$. Due to $a^{3}-b^{3} \\geq 11 a b$ we conclude that $a>b$ so $t$ is a positive integer and the condition can be written as\n\n$$\n11 b(b+t) \\leq t\\left[b^{2}+b(b+t)+(b+t)^{2}\\right] \\leq 12 b(b+t)\n$$\n\nSince\n\n$$\nt\\left[b^{2}+b(b+t)+(b+t)^{2}\\right]=t\\left(b^{2}+b^{2}+b t+b^{2}+2 b t+t^{2}\\right)=3 t b(b+t)+t^{3}\n$$\n\nthe condition can be rewritten as\n\n$$\n(11-3 t) b(b+t) \\leq t^{3} \\leq(12-3 t) b(b+t)\n$$\n\nWe can not have $t \\geq 4$ since in that case $t^{3} \\leq(12-3 t) b(b+t)$ is not satisfied as the right hand side is not positive. Therefore it remains to check the cases when $t \\in\\{1,2,3\\}$. If $t=3$, the above condition becomes\n\n$$\n2 b(b+3) \\leq 27 \\leq 3 b(b+3)\n$$\n\nIf $b \\geq 3$, the left hand side is greater than 27 and if $b=1$ the right hand side is smaller than 27 so there are no solutions in these cases. If $b=2$, we get a solution $(a, b)=(5,2)$.\n\nIf $t \\leq 2$, we have\n\n$$\n(11-3 t) b(b+t) \\geq(11-6) \\cdot 1 \\cdot(1+1)=10>t^{3}\n$$\n\nso there are no solutions in this case.\n\nIn summary, the only solution is $(a, b)=(5,2)$.\n"},"answer":{"kind":"string","value":"(5,2)"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":25,"cells":{"problem":{"kind":"string","value":"\nProblem 2. Let $A B C$ be an acute triangle such that $A H=H D$, where $H$ is the orthocenter of $A B C$ and $D \\in B C$ is the foot of the altitude from the vertex $A$. Let $\\ell$ denote the line through $H$ which is tangent to the circumcircle of the triangle $B H C$. Let $S$ and $T$ be the intersection points of $\\ell$ with $A B$ and $A C$, respectively. Denote the midpoints of $B H$ and $C H$ by $M$ and $N$, respectively. Prove that the lines $S M$ and $T N$ are parallel.\n"},"solution":{"kind":"string","value":"\nSolution 1. In order to prove that $S M$ and $T N$ are parallel, it suffices to prove that both of them are perpendicular to $S T$. Due to symmetry, we will provide a detailed proof of $S M \\perp S T$, whereas the proof of $T N \\perp S T$ is analogous. In this solution we will use the following notation: $\\angle B A C=\\alpha, \\angle A B C=\\beta, \\angle A C B=\\gamma$.\n\n![](https://cdn.mathpix.com/cropped/2024_06_05_6dbeb2bed8a94e31d91eg-3.jpg?height=1047&width=1489&top_left_y=913&top_left_x=318)\n\nWe first observe that, due to the tangency condition, we have\n\n$$\n\\angle S H B=\\angle H C B=90^{\\circ}-\\beta\n$$\n\nCombining the above with\n\n$$\n\\angle S B H=\\angle A B H=90^{\\circ}-\\alpha\n$$\n\nwe get\n\n$$\n\\angle B S H=180^{\\circ}-\\left(90^{\\circ}-\\beta\\right)-\\left(90^{\\circ}-\\alpha\\right)=\\alpha+\\beta=180^{\\circ}-\\gamma\n$$\n\nfrom which it follows that $\\angle A S T=\\gamma$.\n\nSince $A H=H D, H$ is the midpoint of $A D$. If $K$ denotes the midpoint of $A B$, we have that $K H$ and $B C$ are parallel. Since $M$ is the midpoint of $B H$, the lines $K M$ and $A D$ are parallel, from which it follows that $K M$ is perpendicular to $B C$. As $K H$ and $B C$ are parallel, we have that $K M$ is perpendicular to $K H$ so $\\angle M K H=90^{\\circ}$. Using the parallel lines $K H$ and $B C$ we also have\n\n$$\n\\angle K H M=\\angle K H B=\\angle H B C\n$$\n\nNow,\n\n$$\n\\angle H M K=90^{\\circ}-\\angle K H M=90^{\\circ}-\\angle H B C=90^{\\circ}-\\left(90^{\\circ}-\\gamma\\right)=\\gamma=\\angle A S T=\\angle K S H\n$$\n\nso the quadrilateral $M S K H$ is cyclic, which implies that $\\angle M S H=\\angle M K H=90^{\\circ}$. In other words, the lines $S M$ and $S T$ are perpendicular, which completes our proof.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":26,"cells":{"problem":{"kind":"string","value":"\nProblem 4. We call an even positive integer $n$ nice if the set $\\{1,2, \\ldots, n\\}$ can be partitioned into $\\frac{n}{2}$ two-element subsets, such that the sum of the elements in each subset is a power of 3 . For example, 6 is nice, because the set $\\{1,2,3,4,5,6\\}$ can be partitioned into subsets $\\{1,2\\},\\{3,6\\},\\{4,5\\}$. Find the number of nice positive integers which are smaller than $3^{2022}$.\n"},"solution":{"kind":"string","value":"\nSolution. For a nice number $n$ and a given partition of the set $\\{1,2, \\ldots, n\\}$ into twoelement subsets such that the sum of the elements in each subset is a power of 3 , we say that $a, b \\in\\{1,2, \\ldots, n\\}$ are paired if both of them belong to the same subset.\n\nLet $x$ be a nice number and $k$ be a (unique) non-negative integer such that $3^{k} \\leq x3^{k}\n$$\n\nimplies that $s>k$. From these we conclude that $s$ must be equal to $k+1$, so $x+y=3^{k+1}$. The last equation, combined with $x>y$, implies that $x>\\frac{3^{k+1}}{2}$.\n\nSimilarly as above, we can conclude that each number $z$ from the closed interval $\\left[3^{k+1}-x, x\\right]$ is paired with $3^{k+1}-z$. Namely, for any such $z$, the larger of the numbers $z$ and $3^{k+1}-z$ is greater than $\\frac{3^{k+1}}{2}$ which is greater than $3^{k}$, so the numbers $z$ and $3^{k+1}-z$ must necessarily be in the same subset. In other words, each number from the interval $\\left[3^{k+1}-x, x\\right]$ is paired with another number from this interval. Note that this implies that all numbers smaller than $3^{k+1}-x$ are paired among themselves, so the number $3^{k+1}-x-1$ is either nice or equals zero. Also, the number $3^{k}$ must be paired with $2 \\cdot 3^{k}$, so $x \\geq 2 \\cdot 3^{k}$.\n\nFinally, we prove by induction that $a_{n}=2^{n}-1$, where $a_{n}$ is the number of nice positive integers smaller than $3^{n}$. For $n=1$, the claim is obviously true, because 2 is the only nice positive integer smaller than 3 . Now, assume that $a_{n}=2^{n}-1$ for some positive integer $n$. We will prove that $a_{n+1}=2^{n+1}-1$. To prove this, first observe that the number of nice positive integers between $2 \\cdot 3^{n}$ and $3^{n+1}$ is exactly $a_{n+1}-a_{n}$. Next, observe that $3^{n+1}-1$ is nice. For every nice number $2 \\cdot 3^{n} \\leq x<3^{n+1}-1$, the number $3^{n+1}-x-1$ is also nice and is strictly smaller than $3^{n}$. Also, for every positive integer $y<3^{n}$, obviously there is a unique number $x$ such that $2 \\cdot 3^{n} \\leq x<3^{n+1}-1$ and $3^{n+1}-x-1=y$. Thus,\n\n$$\na_{n+1}-a_{n}=a_{n}+1 \\Leftrightarrow a_{n+1}=2 a_{n}+1=2\\left(2^{n}-1\\right)+1=2^{n+1}-1\n$$\n\ncompleting the proof.\n\nIn summary, there are $2^{2022}-1$ nice positive integers smaller than $3^{2022}$.\n\n"},"answer":{"kind":"string","value":"2^{2022}-1"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":27,"cells":{"problem":{"kind":"string","value":"## Problem 1.\n\nFind all pairs $(a, b)$ of positive integers such that $a!+b$ and $b!+a$ are both powers of 5 .\n"},"solution":{"kind":"string","value":"\nSolution. The condition is symmetric so we can assume that $b \\leq a$.\n\nThe first case is when $a=b$. In this case, $a!+a=5^{m}$ for some positive integer $m$. We can rewrite this as $a \\cdot((a-1)!+1)=5^{m}$. This means that $a=5^{k}$ for some integer $k \\geq 0$. It is clear that $k$ cannot be 0 . If $k \\geq 2$, then $(a-1)!+1=5^{l}$ for some $l \\geq 1$, but $a-1=5^{k}-1>5$, so $5 \\mid(a-1)$ !, which is not possible because $5 \\mid(a-1)!+1$. This means that $k=1$ and $a=5$. In this case, $5!+5=125$, which gives us the solution $(5,5)$.\n\nLet us now assume that $1 \\leq b5$, so $5 \\mid a$ !. However, $5 \\mid 5^{y}=a!+1$, which leads to a contradiction. We conclude that $x=1$ and $a=4$. From here $a!+b=25$ and $b!+a=5$, so we get two more solutions: $(1,4)$ and $(4,1)$.\n\nNow we focus on the case $1b$. Because $b \\mid 5^{x}$ and $b>1$, we have $b=5^{z}$ for $z \\geq 1$. If $z \\geq 2$, then $5b=5$, which gives us $a \\geq 10$. However, this would mean that $25|a!, 5| b$ and $25 \\nmid b$, which is not possible, because $a!+b=5^{x}$ and $25 \\mid 5^{x}$.\n\nWe conclude that the only solutions are $(1,4),(4,1)$ and $(5,5)$.\n\n"},"answer":{"kind":"string","value":"(1,4),(4,1),(5,5)"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":28,"cells":{"problem":{"kind":"string","value":"## Problem 2.\n\nProve that for all non-negative real numbers $x, y, z$, not all equal to 0 , the following inequality holds\n\n$$\n\\frac{2 x^{2}-x+y+z}{x+y^{2}+z^{2}}+\\frac{2 y^{2}+x-y+z}{x^{2}+y+z^{2}}+\\frac{2 z^{2}+x+y-z}{x^{2}+y^{2}+z} \\geqslant 3\n$$\n\nDetermine all the triples $(x, y, z)$ for which the equality holds.\n"},"solution":{"kind":"string","value":"\nSolution. Let us first write the expression $L$ on the left hand side in the following way\n\n$$\n\\begin{aligned}\nL & =\\left(\\frac{2 x^{2}-x+y+z}{x+y^{2}+z^{2}}+2\\right)+\\left(\\frac{2 y^{2}+x-y+z}{x^{2}+y+z^{2}}+2\\right)+\\left(\\frac{2 z^{2}+x+y-z}{x^{2}+y^{2}+z}+2\\right)-6 \\\\\n& =\\left(2 x^{2}+2 y^{2}+2 z^{2}+x+y+z\\right)\\left(\\frac{1}{x+y^{2}+z^{2}}+\\frac{1}{x^{2}+y+z^{2}}+\\frac{1}{x^{2}+y^{2}+z}\\right)-6\n\\end{aligned}\n$$\n\nIf we introduce the notation $A=x+y^{2}+z^{2}, B=x^{2}+y+z^{2}, C=x^{2}+y^{2}+z$, then the previous relation becomes\n\n$$\nL=(A+B+C)\\left(\\frac{1}{A}+\\frac{1}{B}+\\frac{1}{C}\\right)-6\n$$\n\nUsing the arithmetic-harmonic mean inequality or Cauchy-Schwartz inequality for positive real numbers $A, B, C$, we easily obtain\n\n$$\n(A+B+C)\\left(\\frac{1}{A}+\\frac{1}{B}+\\frac{1}{C}\\right) \\geqslant 9\n$$\n\nso it holds $L \\geqslant 3$.\n\nThe equality occurs if and only if $A=B=C$, which is equivalent to the system of equations\n\n$$\nx^{2}-y^{2}=x-y, \\quad y^{2}-z^{2}=y-z, \\quad x^{2}-z^{2}=x-z\n$$\n\nIt follows easily that the only solutions of this system are\n\n$(x, y, z) \\in\\{(t, t, t) \\mid t>0\\} \\cup\\{(t, t, 1-t) \\mid t \\in[0,1]\\} \\cup\\{(t, 1-t, t) \\mid t \\in[0,1]\\} \\cup\\{(1-t, t, t) \\mid t \\in[0,1]\\}$.\n\nPSC Remark We feel the equality case needs more explanations in order to have a complete solution, our suggestion follows:\n\nClearly if $x, y, z$ are all equal and not 0 satisfy the condition. Now suppose that not all of them are equal it means we can't simultaneously have $x+y=y+z=z+x=1$ otherwise we would have all $x, y, z$ equal to $\\frac{1}{2}$ which we already discussed. We can suppose now that $x=y$ and $y+z=z+x=1$ where we get $z=1-x$. So, all triples which satisfy the equality are $(x, y, z)=(a, a, a),(b, b, 1-b)$ and all permutations for any $a>0$ and $b \\in[0,1]$\n\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":29,"cells":{"problem":{"kind":"string","value":"## Problem 3.\n\nAlice and Bob play the following game on a $100 \\times 100$ grid, taking turns, with Alice starting first. Initially the grid is empty. At their turn, they choose an integer from 1 to $100^{2}$ that is not written yet in any of the cells and choose an empty cell, and place it in the chosen cell. When there is no empty cell left, Alice computes the sum of the numbers in each row, and her score is the maximum of these 100 sums. Bob computes the sum of the numbers in each column, and his score is the maximum of these 100 sums. Alice wins if her score is greater than Bob's score, Bob wins if his score is greater than Alice's score, otherwise no one wins.\n\nFind if one of the players has a winning strategy, and if so which player has a winning strategy.\n"},"solution":{"kind":"string","value":"\nSolution. We denote by $(i, j)$ the cell in the $i$-th line and in the $j$-th column for every $1 \\leq i, j \\leq n$. Bob associates the following pair of cells : $(i, 2 k+1),(i, 2 k+2)$ for $1 \\leq i \\leq 100$ and $0 \\leq k \\leq 49$ except for $(i, k)=(100,0)$ and $(100,1)$, and the pairs $(100,1),(100,3)$ and $(100,2),(100,4)$.\n\nEach time Alice writes the number $j$ in one of the cell, Bob writes the number $100^{2}+1-j$ in the other cell of the pair.\n\nOne can prove by induction that after each of Bob's turn, for each pair of cell, either there is a number written in each of the cell of the pair, or in neither of them. And that if a number $j$ is written, $100^{2}+1-j$ is also written. Thus Bob can always apply the previous strategy (since $j=100^{2}+1-j$ is impossible).\n\nAt the end, every line has sum $\\left(100^{2}+1\\right) \\times 50$.\n\nAssume by contradiction that Alice can stop Bob from winning if he applies this strategy. Let $c_{j}$ be the sum of the number in the $j$-th column for $1 \\leq j \\leq 100$ : then $c_{j} \\leq 50\\left(100^{2}+1\\right)$. Note that :\n\n$$\n100 \\times 50\\left(100^{2}+1\\right) \\geq c_{1}+\\cdots+c_{100}=1+\\cdots+100^{2}=\\frac{100^{2}\\left(100^{2}+1\\right)}{2}=100 \\times 50\\left(100^{2}+1\\right)\n$$\n\nThus we have equality in the previous inequality : $c_{1}=\\cdots=c_{100}=50\\left(100^{2}+1\\right)$. But if $a$ is the number written in the case $(100,1)$ and $b$ the number written in the case $(100,2)$, then $c_{1}-b+c_{2}-c=99\\left(100^{2}+1\\right)$. Thus $b+c=100\\left(100^{2}+1\\right)-99\\left(100^{2}+1\\right)=100^{2}+1$ : by hypothesis $c$ is also written in the cell $(100,3)$ which is a contradiction.\n\nThus Bob has a winning strategy\n\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":30,"cells":{"problem":{"kind":"string","value":"## Problem 4.\n\nLet $A B C$ be an acute triangle with circumcenter $O$. Let $D$ be the foot of the altitude from $A$ to $B C$ and let $M$ be the midpoint of $O D$. The points $O_{b}$ and $O_{c}$ are the circumcenters of triangles $A O C$ and $A O B$, respectively. If $A O=A D$, prove that the points $A, O_{b}, M$ and $O_{c}$ are concyclic.\n\n"},"solution":{"kind":"string","value":"## Solution.\n\n![](https://cdn.mathpix.com/cropped/2024_06_05_5f128255869e7ca2fe94g-4.jpg?height=1211&width=920&top_left_y=591&top_left_x=568)\n\nNote that $A B=A C$ cannot hold since $A O=A D$ would imply that $O$ is the midpoint of $B C$, which is not possible for an acute triangle. So we may assume without loss of generality that $A B90^{\\circ}$ so that $O_{c}$ is in the interior of triangle $A O B$ and $O_{b}$ in external to the triangles $A O C$ (the other cases are analogous and if $\\angle A O B=90^{\\circ}$ or $\\angle A O C=90^{\\circ}$, then $M_{b} \\equiv O_{b}$ or $M_{c} \\equiv O_{c}$ and we are automatically done). We have\n\n$$\n\\angle M_{c} M_{b} O_{b}=90^{\\circ}+\\angle A M_{b} M_{c}=90^{\\circ}+\\angle A C B\n$$\n\nas well as (since $O_{c} O_{b}$ is a perpendicular bisector of $A O$ and hence bisects $\\angle A O_{C} O$ )\n\n$$\n\\angle M_{c} O_{c} O_{b}=180^{\\circ}-\\angle O O_{c} O_{b}=90^{\\circ}+\\frac{\\angle A O_{c} M_{c}}{2}\n$$\n\n$$\n=90^{\\circ}+\\frac{\\angle A O_{c} B}{4}=90^{\\circ}+\\frac{\\angle A O B}{2}=90^{\\circ}+\\angle A C B\n$$\n\nand therefore $O_{b} M_{b} O_{c} M_{c}$ is cyclic, as desired.\n\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Incomplete"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":31,"cells":{"problem":{"kind":"string","value":"\nProblem 1. Find all triples $(a, b, c)$ of real numbers such that the following system holds:\n\n$$\n\\left\\{\\begin{array}{l}\na+b+c=\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c} \\\\\na^{2}+b^{2}+c^{2}=\\frac{1}{a^{2}}+\\frac{1}{b^{2}}+\\frac{1}{c^{2}}\n\\end{array}\\right.\n$$\n"},"solution":{"kind":"string","value":"\nSolution. First of all if $(a, b, c)$ is a solution of the system then also $(-a,-b,-c)$ is a solution. Hence we can suppose that $a b c>0$. From the first condition we have\n\n$$\na+b+c=\\frac{a b+b c+c a}{a b c}\n$$\n\nNow, from the first condition and the second condition we get\n\n$$\n(a+b+c)^{2}-\\left(a^{2}+b^{2}+c^{2}\\right)=\\left(\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}\\right)^{2}-\\left(\\frac{1}{a^{2}}+\\frac{1}{b^{2}}+\\frac{1}{c^{2}}\\right)\n$$\n\nThe last one simplifies to\n\n$$\na b+b c+c a=\\frac{a+b+c}{a b c}\n$$\n\nFirst we show that $a+b+c$ and $a b+b c+c a$ are different from 0 . Suppose on contrary then from relation (1) or (2) we have $a+b+c=a b+b c+c a=0$. But then we would have\n\n$$\na^{2}+b^{2}+c^{2}=(a+b+c)^{2}-2(a b+b c+c a)=0\n$$\n\nwhich means that $a=b=c=0$. This is not possible since $a, b, c$ should be different from 0 . Now multiplying (1) and (2) we have\n\n$$\n(a+b+c)(a b+b c+c a)=\\frac{(a+b+c)(a b+b c+c a)}{(a b c)^{2}}\n$$\n\nSince $a+b+c$ and $a b+b c+c a$ are different from 0 , we get $(a b c)^{2}=1$ and using the fact that $a b c>0$ we obtain that $a b c=1$. So relations (1) and (2) transform to\n\n$$\na+b+c=a b+b c+c a .\n$$\n\nTherefore,\n\n$$\n(a-1)(b-1)(c-1)=a b c-a b-b c-c a+a+b+c-1=0 \\text {. }\n$$\n\nThis means that at least one of the numbers $a, b, c$ is equal to 1 . Suppose that $c=1$ then relations (1) and (2) transform to $a+b+1=a b+a+b \\Rightarrow a b=1$. Taking $a=t$ then we have $b=\\frac{1}{t}$. We can now verify that any triple $(a, b, c)=\\left(t, \\frac{1}{t}, 1\\right)$ satisfies both conditions. $t \\in \\mathbb{R} \\backslash\\{0\\}$. From the initial observation any triple $(a, b, c)=\\left(t, \\frac{1}{t},-1\\right)$ satisfies both conditions. $t \\in \\mathbb{R} \\backslash\\{0\\}$. So, all triples that satisfy both conditions are $(a, b, c)=\\left(t, \\frac{1}{t}, 1\\right),\\left(t, \\frac{1}{t},-1\\right)$ and all permutations for any $t \\in \\mathbb{R} \\backslash\\{0\\}$.\n\nComment by PSC. After finding that $a b c=1$ and\n\n$$\na+b+c=a b+b c+c a\n$$\n\nwe can avoid the trick considering $(a-1)(b-1)(c-1)$ as follows. By the Vieta's relations we have that $a, b, c$ are roots of the polynomial\n\n$$\nP(x)=x^{3}-s x^{2}+s x-1\n$$\n\nwhich has one root equal to 1 . Then, we can conclude as in the above solution.\n"},"answer":{"kind":"string","value":"(,b,)=(,\\frac{1}{},1),(,\\frac{1}{},-1)"},"problem_type":{"kind":"string","value":"Algebra"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":32,"cells":{"problem":{"kind":"string","value":"\nProblem 2. Let $\\triangle A B C$ be a right-angled triangle with $\\angle B A C=90^{\\circ}$ and let $E$ be the foot of the perpendicular from $A$ on $B C$. Let $Z \\neq A$ be a point on the line $A B$ with $A B=B Z$. Let (c) be the circumcircle of the triangle $\\triangle A E Z$. Let $D$ be the second point of intersection of $(c)$ with $Z C$ and let $F$ be the antidiametric point of $D$ with respect to (c). Let $P$ be the point of intersection of the lines $F E$ and $C Z$. If the tangent to (c) at $Z$ meets $P A$ at $T$, prove that the points $T, E, B, Z$ are concyclic.\n"},"solution":{"kind":"string","value":"\nSolution. We will first show that $P A$ is tangent to $(c)$ at $A$.\n\nSince $E, D, Z, A$ are concyclic, then $\\angle E D C=\\angle E A Z=\\angle E A B$. Since also the triangles $\\triangle A B C$ and $\\triangle E B A$ are similar, then $\\angle E A B=\\angle B C A$, therefore $\\angle E D C=\\angle B C A$.\n\nSince $\\angle F E D=90^{\\circ}$, then $\\angle P E D=90^{\\circ}$ and so\n\n$$\n\\angle E P D=90^{\\circ}-\\angle E D C=90^{\\circ}-\\angle B C A=\\angle E A C\n$$\n\nTherefore the points $E, A, C, P$ are concyclic. It follows that $\\angle C P A=90^{\\circ}$ and therefore the triangle $\\angle P A Z$ is right-angled. Since also $B$ is the midpoint of $A Z$, then $P B=A B=B Z$ and so $\\angle Z P B=$ $\\angle P Z B$.\n\n![](https://cdn.mathpix.com/cropped/2024_06_05_aa04e63f5bdef252b2edg-2.jpg?height=1215&width=1016&top_left_y=1008&top_left_x=530)\n\nFurthermore, $\\angle E P D=\\angle E A C=\\angle C B A=\\angle E B A$ from which it follows that the points $P, E, B, Z$ are also concyclic.\n\nNow observe that\n\n$$\n\\angle P A E=\\angle P C E=\\angle Z P B-\\angle P B E=\\angle P Z B-\\angle P Z E=\\angle E Z B\n$$\n\nTherefore $P A$ is tangent to $(c)$ at $A$ as claimed.\n\nIt now follows that $T A=T Z$. Therefore\n\n$$\n\\begin{aligned}\n\\angle P T Z & =180^{\\circ}-2(\\angle T A B)=180^{\\circ}-2(\\angle P A E+\\angle E A B)=180^{\\circ}-2(\\angle E C P+\\angle A C B) \\\\\n& =180^{\\circ}-2\\left(90^{\\circ}-\\angle P Z B\\right)=2(\\angle P Z B)=\\angle P Z B+\\angle B P Z=\\angle P B A .\n\\end{aligned}\n$$\n\nThus $T, P, B, Z$ are concyclic, and since $P, E, B, Z$ are also concyclic then $T, E, B, Z$ are concyclic as required.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":33,"cells":{"problem":{"kind":"string","value":"\nProblem 3. Alice and Bob play the following game: Alice picks a set $A=\\{1,2, \\ldots, n\\}$ for some natural number $n \\geqslant 2$. Then starting with Bob, they alternatively choose one number from the set $A$, according to the following conditions: initially Bob chooses any number he wants, afterwards the number chosen at each step should be distinct from all the already chosen numbers, and should differ by 1 from an already chosen number. The game ends when all numbers from the set $A$ are chosen. Alice wins if the sum of all of the numbers that she has chosen is composite. Otherwise Bob wins. Decide which player has a winning strategy.\n"},"solution":{"kind":"string","value":"\nSolution. To say that Alice has a winning strategy means that she can find a number $n$ to form the set A, so that she can respond appropriately to all choices of Bob and always get at the end a composite number for the sum of her choices. If such $n$ does not exist, this would mean that Bob has a winning strategy instead.\n\nAlice can try first to check the small values of $n$. Indeed, this gives the following winning strategy for her: she initially picks $n=8$ and responds to all possible choices made by Bob as in the list below (in each row the choices of Bob and Alice are given alternatively, starting with Bob):\n\n$\\begin{array}{llllllll}1 & 2 & 3 & 4 & 5 & 6 & 7 & 8\\end{array}$\n\n$\\begin{array}{llllllll}2 & 3 & 1 & 4 & 5 & 6 & 7 & 8\\end{array}$\n\n$\\begin{array}{llllllll}2 & 3 & 4 & 1 & 5 & 6 & 7 & 8\\end{array}$\n\n$\\begin{array}{llllllll}3 & 2 & 1 & 4 & 5 & 6 & 7 & 8\\end{array}$\n\n$\\begin{array}{llllllll}3 & 2 & 4 & 5 & 1 & 6 & 7 & 8\\end{array}$\n\n$\\begin{array}{llllllll}3 & 2 & 4 & 5 & 6 & 1 & 7 & 8\\end{array}$\n\n$\\begin{array}{llllllll}4 & 5 & 3 & 6 & 2 & 1 & 7 & 8\\end{array}$\n\n$\\begin{array}{llllllll}4 & 5 & 3 & 6 & 7 & 8 & 2 & 1\\end{array}$\n\n$\\begin{array}{llllllll}4 & 5 & 6 & 7 & 3 & 2 & 1 & 8\\end{array}$\n\n$\\begin{array}{llllllll}4 & 5 & 6 & 7 & 3 & 2 & 8 & 1\\end{array}$\n\n$\\begin{array}{llllllll}4 & 5 & 6 & 7 & 8 & 3 & 2 & 1\\end{array}$\n\n$\\begin{array}{llllllll}5 & 4 & 3 & 2 & 1 & 6 & 7 & 8\\end{array}$\n\n$\\begin{array}{llllllll}5 & 4 & 3 & 2 & 6 & 7 & 1 & 8\\end{array}$\n\n$\\begin{array}{llllllll}5 & 4 & 3 & 2 & 6 & 7 & 8 & 1\\end{array}$\n\n$\\begin{array}{llllllll}5 & 4 & 6 & 3 & 2 & 1 & 7 & 8\\end{array}$\n\n$\\begin{array}{llllllll}5 & 4 & 6 & 3 & 7 & 8 & 2 & 1\\end{array}$\n\n$\\begin{array}{llllllll}6 & 7 & 5 & 4 & 3 & 8 & 2 & 1\\end{array}$\n\n$\\begin{array}{llllllll}6 & 7 & 5 & 4 & 8 & 3 & 2 & 1\\end{array}$\n\n$\\begin{array}{llllllll}6 & 7 & 8 & 5 & 4 & 3 & 2 & 1\\end{array}$\n\n$\\begin{array}{llllllll}7 & 6 & 8 & 5 & 4 & 3 & 2 & 1\\end{array}$\n\n$\\begin{array}{llllllll}7 & 6 & 5 & 8 & 4 & 3 & 2 & 1\\end{array}$\n\n$\\begin{array}{llllllll}8 & 7 & 6 & 5 & 4 & 3 & 2 & 1\\end{array}$\n\nIn all cases, Alice's sum is either an even number greater than 2 , or else 15 or 21 , thus Alice always wins.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":34,"cells":{"problem":{"kind":"string","value":"\nProblem 4. Find all pairs $(p, q)$ of prime numbers such that\n\n$$\n1+\\frac{p^{q}-q^{p}}{p+q}\n$$\n\nis a prime number.\n"},"solution":{"kind":"string","value":"\nSolution. It is clear that $p \\neq q$. We set\n\n$$\n1+\\frac{p^{q}-q^{p}}{p+q}=r\n$$\n\nand we have that\n\n$$\np^{q}-q^{p}=(r-1)(p+q)\n$$\n\nFrom Fermat's Little Theorem we have\n\n$$\np^{q}-q^{p} \\equiv-q \\quad(\\bmod p)\n$$\n\nSince we also have that\n\n$$\n(r-1)(p+q) \\equiv-r q-q \\quad(\\bmod p)\n$$\n\nfrom (3) we get that\n\n$$\nr q \\equiv 0 \\quad(\\bmod p) \\Rightarrow p \\mid q r\n$$\n\nhence $p \\mid r$, which means that $p=r$. Therefore, (3) takes the form\n\n$$\np^{q}-q^{p}=(p-1)(p+q)\n$$\n\nWe will prove that $p=2$. Indeed, if $p$ is odd, then from Fermat's Little Theorem we have\n\n$$\np^{q}-q^{p} \\equiv p \\quad(\\bmod q)\n$$\n\nand since\n\n$$\n(p-1)(p+q) \\equiv p(p-1) \\quad(\\bmod q)\n$$\n\nwe have\n\n$$\np(p-2) \\equiv 0 \\quad(\\bmod q) \\Rightarrow q|p(p-2) \\Rightarrow q| p-2 \\Rightarrow q \\leq p-2n^{2}+n+2$. This means that $q \\leq 5$ and the only solution is for $q=5$. Hence the only pair which satisfy the condition is $(p, q)=(2,5)$.\n\nComment by the PSC. From the problem condition, we get that $p^{q}$ should be bigger than $q^{p}$, which gives\n\n$$\nq \\ln p>p \\ln q \\Longleftrightarrow \\frac{\\ln p}{p}>\\frac{\\ln q}{q}\n$$\n\nThe function $\\frac{\\ln x}{x}$ is decreasing for $x>e$, thus if $p$ and $q$ are odd primes, we obtain $q>p$.\n\n"},"answer":{"kind":"string","value":"(2,5)"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":35,"cells":{"problem":{"kind":"string","value":"\nProblem 2. Let $x, y, z$ be positive integers such that $x \\neq y \\neq z \\neq x$. Prove that\n\n$$\n(x+y+z)(x y+y z+z x-2) \\geq 9 x y z\n$$\n\nWhen does the equality hold?\n"},"solution":{"kind":"string","value":"\nSolution. Since $x, y, z$ are distinct positive integers, the required inequality is symmetric and WLOG we can suppose that $x \\geq y+1 \\geq z+2$. We consider 2 possible cases:\n\nCase 1. $y \\geq z+2$. Since $x \\geq y+1 \\geq z+3$ it follows that\n\n$$\n(x-y)^{2} \\geq 1, \\quad(y-z)^{2} \\geq 4, \\quad(x-z)^{2} \\geq 9\n$$\n\nwhich are equivalent to\n\n$$\nx^{2}+y^{2} \\geq 2 x y+1, \\quad y^{2}+z^{2} \\geq 2 y z+4, \\quad x^{2}+z^{2} \\geq 2 x z+9\n$$\n\nor otherwise\n\n$$\nz x^{2}+z y^{2} \\geq 2 x y z+z, \\quad x y^{2}+x z^{2} \\geq 2 x y z+4 x, \\quad y x^{2}+y z^{2} \\geq 2 x y z+9 y\n$$\n\nAdding up the last three inequalities we have\n\n$$\nx y(x+y)+y z(y+z)+z x(z+x) \\geq 6 x y z+4 x+9 y+z\n$$\n\nwhich implies that $(x+y+z)(x y+y z+z x-2) \\geq 9 x y z+2 x+7 y-z$.\n\nSince $x \\geq z+3$ it follows that $2 x+7 y-z \\geq 0$ and our inequality follows.\n\nCase 2. $y=z+1$. Since $x \\geq y+1=z+2$ it follows that $x \\geq z+2$, and replacing $y=z+1$ in the required inequality we have to prove\n\n$$\n(x+z+1+z)(x(z+1)+(z+1) z+z x-2) \\geq 9 x(z+1) z\n$$\n\nwhich is equivalent to\n\n$$\n(x+2 z+1)\\left(z^{2}+2 z x+z+x-2\\right)-9 x(z+1) z \\geq 0\n$$\n\nDoing easy algebraic manipulations, this is equivalent to prove\n\n$$\n(x-z-2)(x-z+1)(2 z+1) \\geq 0\n$$\n\nwhich is satisfied since $x \\geq z+2$.\n\nThe equality is achieved only in the Case 2 for $x=z+2$, so we have equality when $(x, y, z)=$ $(k+2, k+1, k)$ and all the permutations for any positive integer $k$.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":36,"cells":{"problem":{"kind":"string","value":"\nProblem 3. Let $A B C$ be an acute triangle such that $A B \\neq A C$, with circumcircle $\\Gamma$ and circumcenter $O$. Let $M$ be the midpoint of $B C$ and $D$ be a point on $\\Gamma$ such that $A D \\perp B C$. Let $T$ be a point such that $B D C T$ is a parallelogram and $Q$ a point on the same side of $B C$ as $A$ such that\n\n$$\n\\angle B Q M=\\angle B C A \\quad \\text { and } \\quad \\angle C Q M=\\angle C B A\n$$\n\nLet the line $A O$ intersect $\\Gamma$ at $E,(E \\neq A)$ and let the circumcircle of $\\triangle E T Q$ intersect $\\Gamma$ at point $X \\neq E$. Prove that the points $A, M$, and $X$ are collinear.\n"},"solution":{"kind":"string","value":"\nSolution. Let $X^{\\prime}$ be symmetric point to $Q$ in line $B C$. Now since $\\angle C B A=\\angle C Q M=\\angle C X^{\\prime} M$, $\\angle B C A=\\angle B Q M=\\angle B X^{\\prime} M$, we have\n\n$$\n\\angle B X^{\\prime} C=\\angle B X^{\\prime} M+\\angle C X^{\\prime} M=\\angle C B A+\\angle B C A=180^{\\circ}-\\angle B A C\n$$\n\nwe have that $X^{\\prime} \\in \\Gamma$. Now since $\\angle A X^{\\prime} B=\\angle A C B=\\angle M X^{\\prime} B$ we have that $A, M, X^{\\prime}$ are collinear. Note that since\n\n$$\n\\angle D C B=\\angle D A B=90^{\\circ}-\\angle A B C=\\angle O A C=\\angle E A C\n$$\n\nwe get that $D B C E$ is an isosceles trapezoid.\n\n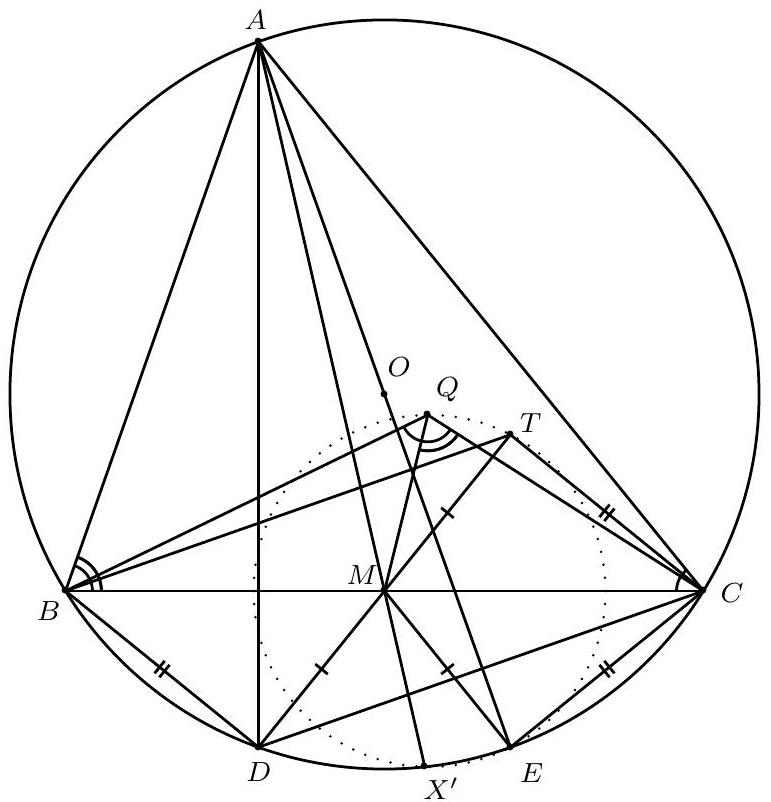![](https://cdn.mathpix.com/cropped/2024_06_05_7b55aeb0100cae01314ag-2.jpg?height=802&width=771&top_left_y=1478&top_left_x=677)\n\nSince $B D C T$ is a parallelogram we have $M T=M D$, with $M, D, T$ being collinear, $B D=C T$, and since $B D E C$ is an isosceles trapezoid we have $B D=C E$ and $M E=M D$. Since\n\n$$\n\\angle B T C=\\angle B D C=\\angle B E D, \\quad C E=B D=C T \\quad \\text { and } \\quad M E=M T\n$$\n\nwe have that $E$ and $T$ are symmetric with respect to the line $B C$. Now since $Q$ and $X^{\\prime}$ are symmetric with respect to the line $B C$ as well, this means that $Q X^{\\prime} E T$ is an isosceles trapezoid which means that $Q, X^{\\prime}, E, T$ are concyclic. Since $X^{\\prime} \\in \\Gamma$ this means that $X \\equiv X^{\\prime}$ and therefore $A, M, X$ are collinear.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":37,"cells":{"problem":{"kind":"string","value":"\nProblem 4. Consider a regular $2 n$-gon $P, A_{1} A_{2} \\ldots A_{2 n}$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We color the sides of $P$ in 3 different colors (ignore the vertices of $P$, we consider them colorless), such that every side is colored in exactly one color, and each color is used at least once. Moreover, from every point in the plane external to $P$, points of at most 2 different colors on $P$ can be seen. Find the number of distinct such colorings of $P$ (two colorings are considered distinct if at least one of the sides is colored differently).\n"},"solution":{"kind":"string","value":"\nSolution Answer: For $n=2$, the answer is 36 ; for $n=3$, the answer is 30 and for $n \\geq 4$, the answer is $6 n$.\n\nLemma 1. Given a regular $2 n$-gon in the plane and a sequence of $n$ consecutive sides $s_{1}, s_{2}, \\ldots, s_{n}$ there is an external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \\ldots, n$.\n\nProof. It is obvious that for a semi-circle $S$, there is a point $R$ in the plane far enough on the bisector of its diameter such that almost the entire semi-circle can be seen from $R$.\n\nNow, it is clear that looking at the circumscribed circle around the $2 n$-gon, there is a semi-circle $S$ such that each $s_{i}$ either has both endpoints on it, or has an endpoint that's on the semi-circle, and is not on the semi-circle's end. So, take $Q$ to be a point in the plane from which almost all of $S$ can be seen, clearly, the color of each $s_{i}$ can be seen from $Q$.\n\nLemma 2. Given a regular $2 n$-gon in the plane, and a sequence of $n+1$ consecutive sides $s_{1}, s_{2}, \\ldots, s_{n+1}$ there is no external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \\ldots, n+1$.\n\nProof. Since $s_{1}$ and $s_{n+1}$ are parallel opposite sides of the $2 n$-gon, they cannot be seen at the same time from an external point.\n\nFor $n=2$, we have a square, so all we have to do is make sure each color is used. Two sides will be of the same color, and we have to choose which are these 2 sides, and then assign colors according to this choice, so the answer is $\\binom{4}{2} .3 .2=36$.\n\nFor $n=3$, we have a hexagon. Denote the sides as $a_{1}, a_{2}, \\ldots q_{6}$, in that order. There must be 2 consecutive sides of different colors, say $a_{1}$ is red, $a_{2}$ is blue. We must have a green side, and only $a_{4}$ and $a_{5}$ can be green. We have 3 possibilities:\n\n1) $a_{4}$ is green, $a_{5}$ is not. So, $a_{3}$ must be blue and $a_{5}$ must be blue (by elimination) and $a_{6}$ must be blue, so we get a valid coloring.\n2) Both $a_{4}$ and $a_{5}$ are green, thus $a_{6}$ must be red and $a_{5}$ must be blue, and we get the coloring rbbggr.\n3) $a_{5}$ is green, $a_{4}$ is not. Then $a_{6}$ must be red. Subsequently, $a_{4}$ must be red (we assume it is not green). It remains that $a_{3}$ must be red, and the coloring is rbrrgr.\n\nThus, we have 2 kinds of configurations:\ni) 2 opposite sides have 2 opposite colors and all other sides are of the third color. This can happen in 3.(3.2.1) $=18$ ways (first choosing the pair of opposite sides, then assigning colors),\n\nii) 3 pairs of consecutive sides, each pair in one of the 3 colors. This can happen in $2.6=12$ ways (2 partitioning into pairs of consecutive sides, for each partitioning, 6 ways to assign the colors).\n\nThus, for $n=3$, the answer is $18+12=30$.\n\nFinally, let's address the case $n \\geq 4$. The important thing now is that any 4 consecutive sides can be seen from an external point, by Lemma 1 .\n\nDenote the sides as $a_{1}, a_{2}, \\ldots, a_{2 n}$. Again, there must be 2 adjacent sides that are of different colors, say $a_{1}$ is blue and $a_{2}$ is red. We must have a green side, and by Lemma 1 , that can only be $a_{n+1}$ or $a_{n+2}$. So, we have 2 cases:\n\nCase 1: $a_{n+1}$ is green, so $a_{n}$ must be red (cannot be green due to Lemma 1 applied to $a_{1}, a_{2}, \\ldots, a_{n}$, cannot be blue for the sake of $a_{2}, \\ldots, a_{n+1}$. If $a_{n+2}$ is red, so are $a_{n+3}, \\ldots, a_{2 n}$, and we get a valid coloring: $a_{1}$ is blue, $a_{n+1}$ is green, and all the others are red.\n\nIf $a_{n+2}$ is green:\na) $a_{n+3}$ cannot be green, because of $a_{2}, a_{1}, a_{2 n} \\ldots, a_{n+3}$.\nb) $a_{n+3}$ cannot be blue, because the 4 adjacent sides $a_{n}, \\ldots, a_{n+3}$ can be seen (this is the case that makes the separate treatment of $n \\geq 4$ necessary)\nc) $a_{n+3}$ cannot be red, because of $a_{1}, a_{2 n}, \\ldots, a_{n+2}$.\n\nSo, in the case that $a_{n+2}$ is also green, we cannot get a valid coloring.\n\nCase 2: $a_{n+2}$ is green is treated the same way as Case 1.\n\nThis means that the only valid configuration for $n \\geq 4$ is having 2 opposite sides colored in 2 different colors, and all other sides colored in the third color. This can be done in $n .3 .2=6 n$ ways.\n\n"},"answer":{"kind":"string","value":"6n"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":38,"cells":{"problem":{"kind":"string","value":"\nProblem 1. Find all prime numbers $a, b, c$ and positive integers $k$ which satisfy the equation\n\n$$\na^{2}+b^{2}+16 \\cdot c^{2}=9 \\cdot k^{2}+1\n$$\n\n"},"solution":{"kind":"string","value":"# Solution: \n\nThe relation $9 \\cdot k^{2}+1 \\equiv 1(\\bmod 3)$ implies\n\n$$\na^{2}+b^{2}+16 \\cdot c^{2} \\equiv 1(\\bmod 3) \\Leftrightarrow a^{2}+b^{2}+c^{2} \\equiv 1(\\bmod 3)\n$$\n\nSince $a^{2} \\equiv 0,1(\\bmod 3), \\quad b^{2} \\equiv 0,1(\\bmod 3), c^{2} \\equiv 0,1(\\bmod 3)$, we have:\n\n| $a^{2}$ | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |\n| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |\n| $b^{2}$ | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |\n| $c^{2}$ | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |\n| $a^{2}+b^{2}+c^{2}$ | 0 | 1 | 1 | 2 | 1 | 2 | 2 | 0 |\n\nFrom the previous table it follows that two of three prime numbers $a, b, c$ are equal to 3 .\n\nCase 1. $a=b=3$\n\nWe have\n\n$$\n\\begin{aligned}\n& a^{2}+b^{2}+16 \\cdot c^{2}=9 \\cdot k^{2}+1 \\Leftrightarrow 9 \\cdot k^{2}-16 \\cdot c^{2}=17 \\Leftrightarrow(3 k-4 c) \\cdot(3 k+4 c)=17, \\\\\n& \\Leftrightarrow\\left\\{\\begin{array} { l } \n{ 3 k - 4 c = 1 , } \\\\\n{ 3 k + 4 c = 1 7 , }\n\\end{array} \\Leftrightarrow \\left\\{\\begin{array}{l}\nc=2, \\\\\nk=3,\n\\end{array} \\text { and } \\quad(a, b, c, k)=(3,3,2,3) .\\right.\\right.\n\\end{aligned}\n$$\n\nCase 2. $c=3$\n\nIf $\\left(3, b_{0}, c, k\\right)$ is a solution of the given equation, then $\\left(b_{0}, 3, c, k\\right)$ is a solution too.\n\nLet $a=3$. We have\n\n$$\na^{2}+b^{2}+16 \\cdot c^{2}=9 \\cdot k^{2}+1 \\Leftrightarrow 9 \\cdot k^{2}-b^{2}=152 \\Leftrightarrow(3 k-b) \\cdot(3 k+b)=152 .\n$$\n\nBoth factors shall have the same parity and we obtain only 2 cases:\n\n- $\\left\\{\\begin{array}{l}3 k-b=2, \\\\ 3 k+b=76,\\end{array} \\Leftrightarrow\\left\\{\\begin{array}{l}b=37, \\\\ k=13,\\end{array}\\right.\\right.$ and $(a, b, c, k)=(3,37,3,13)$;\n- $\\left\\{\\begin{array}{l}3 k-b=4, \\\\ 3 k+b=38,\\end{array} \\Leftrightarrow\\left\\{\\begin{array}{l}b=17, \\\\ k=7,\\end{array}\\right.\\right.$ and $(a, b, c, k)=(3,17,3,7)$.\n\nSo, the given equation has 5 solutions:\n\n$\\{(37,3,3,13),(17,3,3,7),(3,37,3,13),(3,17,3,7),(3,3,2,3)\\}$.\n"},"answer":{"kind":"string","value":"(37,3,3,13),(17,3,3,7),(3,37,3,13),(3,17,3,7),(3,3,2,3)"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":39,"cells":{"problem":{"kind":"string","value":"\nProblem 2. Let $a, b, c$ be positive real numbers such that $a+b+c=3$. Find the minimum value of the expression\n\n$$\nA=\\frac{2-a^{3}}{a}+\\frac{2-b^{3}}{b}+\\frac{2-c^{3}}{c}\n$$\n\n![](https://cdn.mathpix.com/cropped/2024_06_05_f56efd4e6fb711c0f78eg-2.jpg?height=348&width=477&top_left_y=109&top_left_x=241)\n\n$19^{\\text {th }}$ Junior Balkan Mathematical Olympiad June 24-29, 2015, Belgrade, Serbia\n\n"},"solution":{"kind":"string","value":"## Solution:\n\nWe can rewrite $A$ as follows:\n\n$$\n\\begin{aligned}\n& A=\\frac{2-a^{3}}{a}+\\frac{2-b^{3}}{b}+\\frac{2-c^{3}}{c}=2\\left(\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}\\right)-a^{2}-b^{2}-c^{2}= \\\\\n& 2\\left(\\frac{a b+b c+c a}{a b c}\\right)-\\left(a^{2}+b^{2}+c^{2}\\right)=2\\left(\\frac{a b+b c+c a}{a b c}\\right)-\\left((a+b+c)^{2}-2(a b+b c+c a)\\right)= \\\\\n& 2\\left(\\frac{a b+b c+c a}{a b c}\\right)-(9-2(a b+b c+c a))=2\\left(\\frac{a b+b c+c a}{a b c}\\right)+2(a b+b c+c a)-9= \\\\\n& 2(a b+b c+c a)\\left(\\frac{1}{a b c}+1\\right)-9\n\\end{aligned}\n$$\n\nRecall now the well-known inequality $(x+y+z)^{2} \\geq 3(x y+y z+z x)$ and set $x=a b, y=b c, z=c a$, to obtain $(a b+b c+c a)^{2} \\geq 3 a b c(a+b+c)=9 a b c$, where we have used $a+b+c=3$. By taking the square roots on both sides of the last one we obtain:\n\n$$\na b+b c+c a \\geq 3 \\sqrt{a b c}\n$$\n\nAlso by using AM-GM inequality we get that\n\n$$\n\\frac{1}{a b c}+1 \\geq 2 \\sqrt{\\frac{1}{a b c}}\n$$\n\nMultiplication of (1) and (2) gives:\n\n$$\n(a b+b c+c a)\\left(\\frac{1}{a b c}+1\\right) \\geq 3 \\sqrt{a b c} \\cdot 2 \\sqrt{\\frac{1}{a b c}}=6\n$$\n\nSo $A \\geq 2 \\cdot 6-9=3$ and the equality holds if and only if $a=b=c=1$, so the minimum value is 3.\n"},"answer":{"kind":"string","value":"3"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":40,"cells":{"problem":{"kind":"string","value":"\nProblem 3. Let $\\triangle A B C$ be an acute triangle. The lines $l_{1}, l_{2}$ are perpendicular to $A B$ at the points $A, B$ respectively. The perpendicular lines from the midpoint $M$ of $A B$ to the sides of the triangle $A C, B C$ intersect the lines $l_{1}, l_{2}$ at the points $E, F$, respectively. If $D$ is the intersection point of $E F$ and $M C$, prove that\n\n$$\n\\angle A D B=\\angle E M F\n$$\n\n"},"solution":{"kind":"string","value":"## Solution:\n\nLet $H, G$ be the points of intersection of $M E, M F$ with $A C, B C$ respectively. From the similarity of triangles $\\triangle M H A$ and $\\triangle M A E$ we get $\\frac{M H}{M A}=\\frac{M A}{M E}$, thus\n\n$$\nM A^{2}=M H \\cdot M E\n$$\n\nSimilarly, from the similarity of triangles $\\triangle M B G$ and $\\triangle M F B$ we get $\\frac{M B}{M F}=\\frac{M G}{M B}$, thus\n\n$$\nM B^{2}=M F \\cdot M G\n$$\n\nSince $M A=M B$, from (1), (2), we conclude that the points $E, H, G, F$ are concyclic.\n![](https://cdn.mathpix.com/cropped/2024_06_05_f56efd4e6fb711c0f78eg-3.jpg?height=1040&width=1220&top_left_y=110&top_left_x=226)\n\nTherefore, we get that $\\angle F E H=\\angle F E M=\\angle H G M$. Also, the quadrilateral $C H M G$ is cyclic, so $\\angle C M H=\\angle H G C$. We have\n\n$$\n\\angle F E H+\\angle C M H=\\angle H G M+\\angle H G C=90^{\\circ}\n$$\n\nthus $C M \\perp E F$. Now, from the cyclic quadrilaterals $F D M B$ and $E A M D$, we get that $\\angle D F M=\\angle D B M$ and $\\angle D E M=\\angle D A M$. Therefore, the triangles $\\triangle E M F$ and $\\triangle A D B$ are similar, so $\\angle A D B=\\angle E M F$.\n\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":41,"cells":{"problem":{"kind":"string","value":"## Problem 4.\n\nAn $L$-figure is one of the following four pieces, each consisting of three unit squares:\n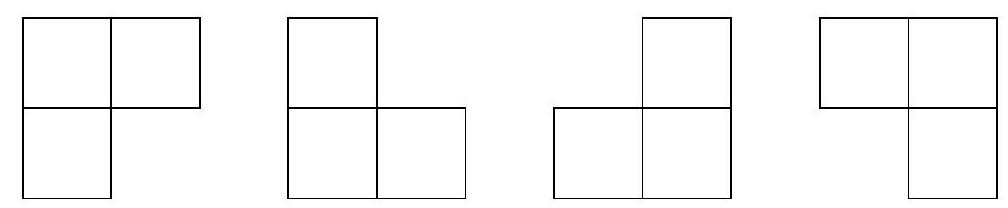![](https://cdn.mathpix.com/cropped/2024_06_05_f56efd4e6fb711c0f78eg-3.jpg?height=208&width=1008&top_left_y=1692&top_left_x=524)\n\nA $5 \\times 5$ board, consisting of 25 unit squares, a positive integer $k \\leq 25$ and an unlimited supply $L$-figures are given. Two players, $\\boldsymbol{A}$ and $\\boldsymbol{B}$, play the following game: starting with $\\boldsymbol{A}$ they alternatively mark a previously unmarked unit square until they marked a total of $k$ unit squares.\n\nWe say that a placement of $L$-figures on unmarked unit squares is called good if the $L$-figure do not overlap and each of them covers exactly three unmarked unit squares of the board. $\\boldsymbol{B}$ wins if every $\\boldsymbol{g o o d}$ placement of $L$-figures leaves uncovered at least three unmarked unit squares. Determine the minimum value of $k$ for which $\\boldsymbol{B}$ has a winning strategy.\n\n"},"solution":{"kind":"string","value":"## Solution:\n\nWe will show that player $\\boldsymbol{A}$ wins if $k=1,2,3$, but player $\\boldsymbol{B}$ wins if $k=4$. Thus the smallest $k$ for which $\\boldsymbol{B}$ has a winning strategy exists and is equal to 4 .\n\nIf $k=1$, player $\\boldsymbol{A}$ marks the upper left corner of the square and then fills it as follows.\n\n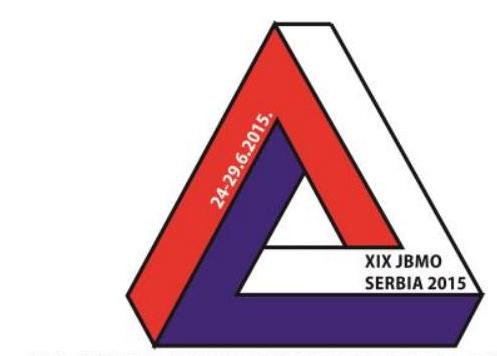![](https://cdn.mathpix.com/cropped/2024_06_05_f56efd4e6fb711c0f78eg-4.jpg?height=356&width=497&top_left_y=105&top_left_x=223)\n\n## $19^{\\text {th }}$ Junior Balkan Mathematical Olympiad\n\n June 24-29, 2015, Belgrade, Serbia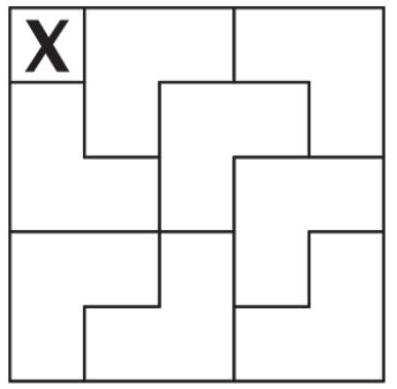![](https://cdn.mathpix.com/cropped/2024_06_05_f56efd4e6fb711c0f78eg-4.jpg?height=389&width=397&top_left_y=568&top_left_x=835)\n\nIf $k=2$, player $\\boldsymbol{A}$ marks the upper left corner of the square. Whatever square player $\\boldsymbol{B}$ marks, then player $\\boldsymbol{A}$ can fill in the square in exactly the same pattern as above except that he doesn't put the $L$-figure which covers the marked square of $\\boldsymbol{B}$. Player $\\boldsymbol{A}$ wins because he has left only two unmarked squares uncovered.\n\nFor $k=3$, player $\\boldsymbol{A}$ wins by following the same strategy. When he has to mark a square for the second time, he marks any yet unmarked square of the $L$-figure that covers the marked square of $\\boldsymbol{B}$.\n\nLet us now show that for $k=4$ player $\\boldsymbol{B}$ has a winning strategy. Since there will be 21 unmarked squares, player $\\boldsymbol{A}$ will need to cover all of them with seven $L$-figures. We can assume that in his first move, player $\\boldsymbol{A}$ does not mark any square in the bottom two rows of the chessboard (otherwise just rotate the chessboard). In his first move player $\\boldsymbol{B}$ marks the square labeled 1 in the following figure.\n\n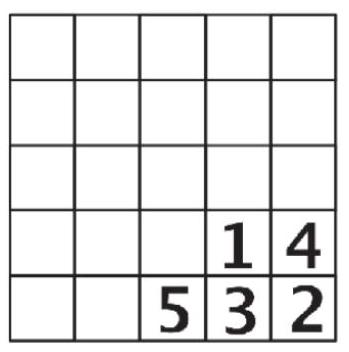![](https://cdn.mathpix.com/cropped/2024_06_05_f56efd4e6fb711c0f78eg-4.jpg?height=352&width=349&top_left_y=1623&top_left_x=859)\n\nIf player $\\boldsymbol{A}$ in his next move does not mark any of the squares labeled 2,3 and 4 then player $\\boldsymbol{B}$ marks the square labeled 3 . Player $\\boldsymbol{B}$ wins as the square labeled 2 is left unmarked but cannot be covered with an $L$-figure.\n\nIf player $\\boldsymbol{A}$ in his next move marks the square labeled 2, then player $\\boldsymbol{B}$ marks the square labeled 5. Player $\\boldsymbol{B}$ wins as the square labeled 3 is left unmarked but cannot be covered with an $L$-figure.\n\nFinally, if player $\\boldsymbol{A}$ in his next move marks one of the squares labeled 3 or 4, player $\\boldsymbol{B}$ marks the other of these two squares. Player $\\boldsymbol{B}$ wins as the square labeled 2 is left unmarked but cannot be covered with an $L$-figure.\n\nSince we have covered all possible cases, player $\\boldsymbol{B}$ wins when $k=4$.\n\n"},"answer":{"kind":"string","value":"4"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Incomplete"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":42,"cells":{"problem":{"kind":"string","value":"\nA1. Let $a, b, c$ be positive real numbers such that $a+b+c+a b+b c+c a+a b c=7$. Prove that\n\n$$\n\\sqrt{a^{2}+b^{2}+2}+\\sqrt{b^{2}+c^{2}+2}+\\sqrt{c^{2}+a^{2}+2} \\geq 6\n$$\n"},"solution":{"kind":"string","value":"\nSolution. First we see that $x^{2}+y^{2}+1 \\geq x y+x+y$. Indeed, this is equivalent to\n\n$$\n(x-y)^{2}+(x-1)^{2}+(y-1)^{2} \\geq 0\n$$\n\nTherefore\n\n$$\n\\begin{aligned}\n& \\sqrt{a^{2}+b^{2}+2}+\\sqrt{b^{2}+c^{2}+2}+\\sqrt{c^{2}+a^{2}+2} \\\\\n\\geq & \\sqrt{a b+a+b+1}+\\sqrt{b c+b+c+1}+\\sqrt{c a+c+a+1} \\\\\n= & \\sqrt{(a+1)(b+1)}+\\sqrt{(b+1)(a+1)}+\\sqrt{(c+1)(a+1)}\n\\end{aligned}\n$$\n\nIt follows from the AM-GM inequality that\n\n$$\n\\begin{aligned}\n& \\sqrt{(a+1)(b+1)}+\\sqrt{(b+1)(a+1)}+\\sqrt{(c+1)(a+1)} \\\\\n\\geq & 3 \\sqrt[3]{\\sqrt{(a+1)(b+1)} \\cdot \\sqrt{(b+1)(a+1)} \\cdot \\sqrt{(c+1)(a+1)}} \\\\\n= & 3 \\sqrt[3]{(a+1)(b+1)(c+1)}\n\\end{aligned}\n$$\n\nOn the other hand, the given condition is equivalent to $(a+1)(b+1)(c+1)=8$ and we get the desired inequality.\n\nObviously, equality is attained if and only if $a=b=c=1$.\n\nRemark. The condition of positivity of $a, b, c$ is superfluous and the equality $\\cdots=7$ can be replaced by the inequality $\\cdots \\geq 7$. Indeed, the above proof and the triangle inequality imply that\n\n$$\n\\begin{aligned}\n\\sqrt{a^{2}+b^{2}+2}+\\sqrt{b^{2}+c^{2}+2}+\\sqrt{c^{2}+a^{2}+2} & \\geq 3 \\sqrt[3]{(|a|+1)(|b|+1)(|c|+1)} \\\\\n& \\geq 3 \\sqrt[3]{|a+1| \\cdot|b+1| \\cdot|c+1|} \\geq 6\n\\end{aligned}\n$$\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":43,"cells":{"problem":{"kind":"string","value":"\nA2. Let $a$ and $b$ be positive real numbers such that $3 a^{2}+2 b^{2}=3 a+2 b$. Find the minimum value of\n\n$$\nA=\\sqrt{\\frac{a}{b(3 a+2)}}+\\sqrt{\\frac{b}{a(2 b+3)}}\n$$\n"},"solution":{"kind":"string","value":"\nSolution. By the Cauchy-Schwarz inequality we have that\n\n$$\n5\\left(3 a^{2}+2 b^{2}\\right)=5\\left(a^{2}+a^{2}+a^{2}+b^{2}+b^{2}\\right) \\geq(3 a+2 b)^{2}\n$$\n\n(or use that the last inequality is equivalent to $(a-b)^{2} \\geq 0$ ).\n\nSo, with the help of the given condition we get that $3 a+2 b \\leq 5$. Now, by the AM-GM inequality we have that\n\n$$\nA \\geq 2 \\sqrt{\\sqrt{\\frac{a}{b(3 a+2)}} \\cdot \\sqrt{\\frac{b}{a(2 b+3)}}}=\\frac{2}{\\sqrt[4]{(3 a+2)(2 b+3)}}\n$$\n\nFinally, using again the AM-GM inequality, we get that\n\n$$\n(3 a+2)(2 b+3) \\leq\\left(\\frac{3 a+2 b+5}{2}\\right)^{2} \\leq 25\n$$\n\nso $A \\geq 2 / \\sqrt{5}$ and the equality holds if and only if $a=b=1$.\n"},"answer":{"kind":"string","value":"\\frac{2}{\\sqrt{5}}"},"problem_type":{"kind":"string","value":"Algebra"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":44,"cells":{"problem":{"kind":"string","value":"\nA3. Let $a, b, c, d$ be real numbers such that $0 \\leq a \\leq b \\leq c \\leq d$. Prove the inequality\n\n$$\na b^{3}+b c^{3}+c d^{3}+d a^{3} \\geq a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\n$$\n"},"solution":{"kind":"string","value":"\nSolution. The inequality is equivalent to\n\n$$\n\\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\\right)^{2} \\geq\\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\\right)^{2}\n$$\n\nBy the Cauchy-Schwarz inequality,\n\n$$\n\\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\\right)\\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\\right) \\geq\\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\\right)^{2}\n$$\n\nHence it is sufficient to prove that\n\n$$\n\\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\\right)^{2} \\geq\\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\\right)\\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\\right)\n$$\n\ni.e. to prove $a b^{3}+b c^{3}+c d^{3}+d a^{3} \\geq a^{3} b+b^{3} c+c^{3} d+d^{3} a$.\n\nThis inequality can be written successively\n\n$$\na\\left(b^{3}-d^{3}\\right)+b\\left(c^{3}-a^{3}\\right)+c\\left(d^{3}-b^{3}\\right)+d\\left(a^{3}-c^{3}\\right) \\geq 0\n$$\n\nor\n\n$$\n(a-c)\\left(b^{3}-d^{3}\\right)-(b-d)\\left(a^{3}-c^{3}\\right) \\geq 0\n$$\n\nwhich comes down to\n\n$$\n(a-c)(b-d)\\left(b^{2}+b d+d^{2}-a^{2}-a c-c^{2}\\right) \\geq 0\n$$\n\nThe last inequality is true because $a-c \\leq 0, b-d \\leq 0$, and $\\left(b^{2}-a^{2}\\right)+(b d-a c)+\\left(d^{2}-c^{2}\\right) \\geq 0$ as a sum of three non-negative numbers.\n\nThe last inequality is satisfied with equality whence $a=b$ and $c=d$. Combining this with the equality cases in the Cauchy-Schwarz inequality we obtain the equality cases for the initial inequality: $a=b=c=d$.\n\nRemark. Instead of using the Cauchy-Schwarz inequality, once the inequality $a b^{3}+b c^{3}+c d^{3}+$ $d a^{3} \\geq a^{3} b+b^{3} c+c^{3} d+d^{3} a$ is established, we have $2\\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\\right) \\geq\\left(a b^{3}+b c^{3}+c d^{3}+\\right.$ $\\left.d a^{3}\\right)+\\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\\right)=\\left(a b^{3}+a^{3} b\\right)+\\left(b c^{3}+b^{3} c\\right)+\\left(c d^{3}+c^{3} d\\right)+\\left(d a^{3}+d^{3} a\\right) \\stackrel{A M-G M}{\\geq}$ $2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} d^{2}+2 d^{2} a^{2}$ which gives the conclusion.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":45,"cells":{"problem":{"kind":"string","value":"\nA4. Let $x, y, z$ be three distinct positive integers. Prove that\n\n$$\n(x+y+z)(x y+y z+z x-2) \\geq 9 x y z\n$$\n\nWhen does the equality hold?\n"},"solution":{"kind":"string","value":"\nSolution. Since $x, y, z$ are distinct positive integers, the required inequality is symmetric and WLOG we can suppose that $x \\geq y+1 \\geq z+2$. We consider 2 possible cases:\n\nCase 1. $y \\geq z+2$. Since $x \\geq y+1 \\geq z+3$ it follows that\n\n$$\n(x-y)^{2} \\geq 1, \\quad(y-z)^{2} \\geq 4, \\quad(x-z)^{2} \\geq 9\n$$\n\nwhich are equivalent to\n\n$$\nx^{2}+y^{2} \\geq 2 x y+1, \\quad y^{2}+z^{2} \\geq 2 y z+4, \\quad x^{2}+z^{2} \\geq 2 x z+9\n$$\n\nor otherwise\n\n$$\nz x^{2}+z y^{2} \\geq 2 x y z+z, \\quad x y^{2}+x z^{2} \\geq 2 x y z+4 x, \\quad y x^{2}+y z^{2} \\geq 2 x y z+9 y\n$$\n\nAdding up the last three inequalities we have\n\n$$\nx y(x+y)+y z(y+z)+z x(z+x) \\geq 6 x y z+4 x+9 y+z\n$$\n\nwhich implies that $(x+y+z)(x y+y z+z x-2) \\geq 9 x y z+2 x+7 y-z$.\n\nSince $x \\geq z+3$ it follows that $2 x+7 y-z \\geq 0$ and our inequality follows.\n\nCase 2. $y=z+1$. Since $x \\geq y+1=z+2$ it follows that $x \\geq z+2$, and replacing $y=z+1$ in the required inequality we have to prove\n\n$$\n(x+z+1+z)(x(z+1)+(z+1) z+z x-2) \\geq 9 x(z+1) z\n$$\n\nwhich is equivalent to\n\n$$\n(x+2 z+1)\\left(z^{2}+2 z x+z+x-2\\right)-9 x(z+1) z \\geq 0\n$$\n\nDoing easy algebraic manipulations, this is equivalent to prove\n\n$$\n(x-z-2)(x-z+1)(2 z+1) \\geq 0\n$$\n\nwhich is satisfied since $x \\geq z+2$.\n\nThe equality is achieved only in the Case 2 for $x=z+2$, so we have equality when $(x, y, z)=$ $(k+2, k+1, k)$ and all the permutations for any positive integer $k$.\n\n## Combinatorics\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":46,"cells":{"problem":{"kind":"string","value":"\nC1. Consider a regular $2 n+1$-gon $P$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We want to color the sides of $P$ in 3 colors, such that every side is colored in exactly one color, and each color must be used at least once. Moreover, from every point in the plane external to $P$, at most 2 different colors on $P$ can be seen (ignore the vertices of $P$, we consider them colorless). Find the largest positive integer for which such a coloring is possible.\n"},"solution":{"kind":"string","value":"\nSolution. Answer: $n=1$ is clearly a solution, we can just color each side of the equilateral triangle in a different color, and the conditions are satisfied. We prove there is no larger $n$ that fulfills the requirements.\n\nLemma 1. Given a regular $2 n+1$-gon in the plane, and a sequence of $n+1$ consecutive sides $s_{1}, s_{2}, \\ldots, s_{n+1}$ there is an external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \\ldots, n+1$.\n\nProof. It is obvious that for a semi-circle $S$, there is a point $R$ in the plane far enough on the perpendicular bisector of the diameter of $S$ such that almost the entire semi-circle can be seen from $R$.\n\nNow, it is clear that looking at the circumscribed circle around the $2 n+1$-gon, there is a semi-circle $S$ such that each $s_{i}$ either has both endpoints on it, or has an endpoint that is on the semi-circle, and is not on the semicircle's end. So, take $Q$ to be a point in the plane from which almost all of $S$ can be seen, clearly, the color of each $s_{i}$ can be seen from $Q$. $\\diamond$ Take $n \\geq 2$, denote the sides $a_{1}, a_{2}, \\ldots, a_{2 n+1}$ in that order, and suppose we have a coloring that satisfies the condition of the problem. Let's call the 3 colors red, green and blue. We must have 2 adjacent sides of different colors, say $a_{1}$ is red and $a_{2}$ is green. Then, by Lemma 1 :\n\n(i) We cannot have a blue side among $a_{1}, a_{2}, \\ldots, a_{n+1}$.\n(ii) We cannot have a blue side among $a_{2}, a_{1}, a_{2 n+1}, \\ldots, a_{n+3}$.\n\nWe are required to have at least one blue side, and according to 1 ) and 2), that can only be $a_{n+2}$, so $a_{n+2}$ is blue. Now, applying Lemma 1 on the sequence of sides $a_{2}, a_{3}, \\ldots, a_{n+2}$ we get that $a_{2}, a_{3}, \\ldots, a_{n+1}$ are all green. Applying Lemma 1 on the sequence of sides $a_{1}, a_{2 n+1}, a_{2 n}, \\ldots, a_{n+2}$ we get that $a_{2 n+1}, a_{2 n}, \\ldots, a_{n+3}$ are all red.\n\nTherefore $a_{n+1}, a_{n+2}$ and $a_{n+3}$ are all of different colors, and for $n \\geq 2$ they can all be seen from the same point according to Lemma 1 , so we have a contradiction.\n"},"answer":{"kind":"string","value":"1"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":47,"cells":{"problem":{"kind":"string","value":"\nC2. Consider a regular $2 n$-gon $P$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We want to color the sides of $P$ in 3 colors, such that every side is colored in exactly one color, and each color must be used at least once. Moreover, from every point in the plane external to $P$, at most 2 different colors on $P$ can be seen (ignore the vertices of $P$, we consider them colorless). Find the number of distinct such colorings of $P$ (two colorings are considered distinct if at least one side is colored differently).\n"},"solution":{"kind":"string","value":"\nSolution. Answer: For $n=2$, the answer is 36 ; for $n=3$, the answer is 30 and for $n \\geq 4$, the answer is $6 n$.\n\nLemma 1. Given a regular $2 n$-gon in the plane and a sequence of $n$ consecutive sides $s_{1}, s_{2}, \\ldots, s_{n}$ there is an external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \\ldots, n$.\n\nProof. It is obvious that for a semi-circle $S$, there is a point $R$ in the plane far enough on the bisector of its diameter such that almost the entire semi-circle can be seen from $R$.\n\nNow, it is clear that looking at the circumscribed circle around the $2 n$-gon, there is a semi-circle $S$ such that each $s_{i}$ either has both endpoints on it, or has an endpoint that's on the semi-circle, and is not on the semi-circle's end. So, take $Q$ to be a point in the plane from which almost all of $S$ can be seen, clearly, the color of each $s_{i}$ can be seen from $Q$.\n\nLemma 2. Given a regular $2 n$-gon in the plane, and a sequence of $n+1$ consecutive sides $s_{1}, s_{2}, \\ldots, s_{n+1}$ there is no external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \\ldots, n+1$.\n\nProof. Since $s_{1}$ and $s_{n+1}$ are parallel opposite sides of the $2 n$-gon, they cannot be seen at the same time from an external point.\n\nFor $n=2$, we have a square, so all we have to do is make sure each color is used. Two sides will be of the same color, and we have to choose which are these 2 sides, and then assign colors\naccording to this choice, so the answer is $\\binom{4}{2} \\cdot 3 \\cdot 2=36$.\n\nFor $n=3$, we have a hexagon. Denote the sides as $a_{1}, a_{2}, \\ldots q_{6}$, in that order. There must be 2 consecutive sides of different colors, say $a_{1}$ is red, $a_{2}$ is blue. We must have a green side, and only $a_{4}$ and $a_{5}$ can be green. We have 3 possibilities:\n\n1) $a_{4}$ is green, $a_{5}$ is not. So, $a_{3}$ must be blue and $a_{5}$ must be blue (by elimination) and $a_{6}$ must be blue, so we get a valid coloring.\n2) Both $a_{4}$ and $a_{5}$ are green, thus $a_{6}$ must be red and $a_{5}$ must be blue, and we get the coloring rbbggr.\n3) $a_{5}$ is green, $a_{4}$ is not. Then $a_{6}$ must be red. Subsequently, $a_{4}$ must be red (we assume it is not green). It remains that $a_{3}$ must be red, and the coloring is rbrrgr.\n\nThus, we have 2 kinds of configurations:\n\ni) 2 opposite sides have 2 opposite colors and all other sides are of the third color. This can happen in 3.(3.2.1) $=18$ ways (first choosing the pair of opposite sides, then assigning colors), ii) 3 pairs of consecutive sides, each pair in one of the 3 colors. This can happen in $2.6=12$ ways (2 partitioning into pairs of consecutive sides, for each partitioning, 6 ways to assign the colors).\n\nThus, for $n=3$, the answer is $18+12=30$.\n\nFinally, let's address the case $n \\geq 4$. The important thing now is that any 4 consecutive sides can be seen from an external point, by Lemma 1.\n\nDenote the sides as $a_{1}, a_{2}, \\ldots, a_{2 n}$. Again, there must be 2 adjacent sides that are of different colors, say $a_{1}$ is blue and $a_{2}$ is red. We must have a green side, and by Lemma 1, that can only be $a_{n+1}$ or $a_{n+2}$. So, we have 2 cases:\n\nCase 1: $a_{n+1}$ is green, so $a_{n}$ must be red (cannot be green due to Lemma 1 applied to $a_{1}, a_{2}, \\ldots, a_{n}$, cannot be blue for the sake of $a_{2}, \\ldots, a_{n+1}$. If $a_{n+2}$ is red, so are $a_{n+3}, \\ldots, a_{2 n}$, and we get a valid coloring: $a_{1}$ is blue, $a_{n+1}$ is green, and all the others are red.\n\nIf $a_{n+2}$ is green:\n\na) $a_{n+3}$ cannot be green, because of $a_{2}, a_{1}, a_{2 n} \\ldots, a_{n+3}$.\nb) $a_{n+3}$ cannot be blue, because the 4 adjacent sides $a_{n}, \\ldots, a_{n+3}$ can be seen (this is the case that makes the separate treatment of $n \\geq 4$ necessary)\n\nc) $a_{n+3}$ cannot be red, because of $a_{1}, a_{2 n}, \\ldots, a_{n+2}$.\n\nSo, in the case that $a_{n+2}$ is also green, we cannot get a valid coloring.\n\nCase 2: $a_{n+2}$ is green is treated the same way as Case 1.\n\nThis means that the only valid configuration for $n \\geq 4$ is having 2 opposite sides colored in 2 different colors, and all other sides colored in the third color. This can be done in $n \\cdot 3 \\cdot 2=6 n$ ways.\n"},"answer":{"kind":"string","value":"6n"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":48,"cells":{"problem":{"kind":"string","value":"\nC3. We have two piles with 2000 and 2017 coins respectively. Ann and Bob take alternate turns making the following moves: The player whose turn is to move picks a pile with at least two coins, removes from that pile $t$ coins for some $2 \\leqslant t \\leqslant 4$, and adds to the other pile 1 coin. The players can choose a different $t$ at each turn, and the player who cannot make a move loses. If Ann plays first determine which player has a winning strategy.\n"},"solution":{"kind":"string","value":"\nSolution. Denote the number of coins in the two piles by $X$ and $Y$. We say that the pair $(X, Y)$ is losing if the player who begins the game loses and that the pair $(X, Y)$ is winning otherwise. We shall prove that $(X, Y)$ is loosing if $X-Y \\equiv 0,1,7 \\bmod 8$, and winning if $X-Y \\equiv 2,3,4,5,6 \\bmod 8$.\n\nLemma 1. If we have a winning pair $(X, Y)$ then we can always play in such a way that the other player is then faced with a losing pair.\n\nProof of Lemma 1. Assume $X \\geq Y$ and write $X=Y+8 k+\\ell$ for some non-negative integer $k$ and some $\\ell \\in\\{2,3,4,5,6\\}$. If $\\ell=2,3,4$ then we remove two coins from the first pile and add one coin to the second pile. If $\\ell=5,6$ then we remove four coins from the first pile and add one coin to the second pile. In each case we then obtain loosing pair\n\nLemma 2. If we are faced with a losing distribution then either we cannot play, or, however we play, the other player is faced with a winning distribution.\n\nProof of Lemma 2. Without loss of generality we may assume that we remove $k$ coins from the first pile. The following table show the new difference for all possible values of $k$ and all possible differences $X-Y$. So however we move, the other player will be faced with a winning distribution.\n\n| $k \\backslash X-Y$ | 0 | 1 | 7 |\n| :---: | :---: | :---: | :---: |\n| 2 | 5 | 6 | 4 |\n| 3 | 4 | 5 | 3 |\n| 4 | 3 | 4 | 2 |\n\nSince initially the coin difference is 1 mod 8 , by Lemmas 1 and 2 Bob has a winning strategy: He can play so that he is always faced with a winning distribution while Ann is always faced with a losing distribution. So Bob cannot lose. On the other hand the game finishes after at most 4017 moves, so Ann has to lose.\n\n## Geometry\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":49,"cells":{"problem":{"kind":"string","value":"\nG1. Given a parallelogram $A B C D$. The line perpendicular to $A C$ passing through $C$ and the line perpendicular to $B D$ passing through $A$ intersect at point $P$. The circle centered at point $P$ and radius $P C$ intersects the line $B C$ at point $X,(X \\neq C)$ and the line $D C$ at point $Y$, $(Y \\neq C)$. Prove that the line $A X$ passes through the point $Y$.\n"},"solution":{"kind":"string","value":"\nSolution. Denote the feet of the perpendiculars from $P$ to the lines $B C$ and $D C$ by $M$ and $N$ respectively and let $O=A C \\cap B D$. Since the points $O, M$ and $N$ are midpoints of $C A, C X$ and $C Y$ respectively it suffices to prove that $M, N$ and $O$ are collinear. According to Menelaus's theorem for $\\triangle B C D$ and points $M, N$ and $O$ we have to prove that\n\n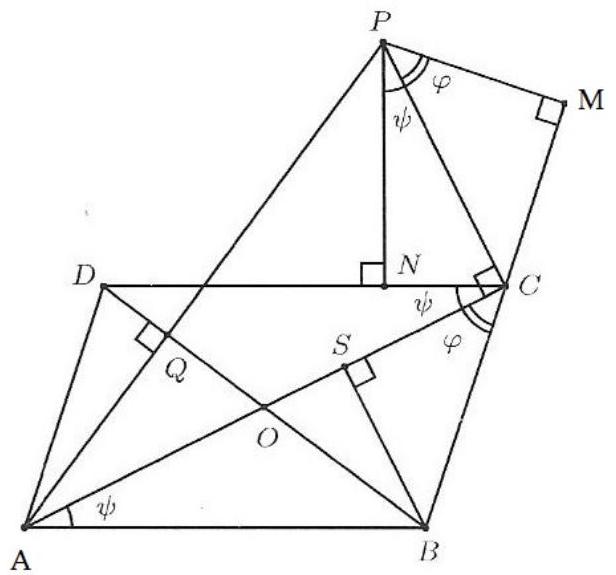![](https://cdn.mathpix.com/cropped/2024_06_05_7db2aacb858e7f253ee0g-11.jpg?height=575&width=616&top_left_y=905&top_left_x=1226)\n\n$$\n\\frac{B M}{M C} \\cdot \\frac{C N}{N D} \\cdot \\frac{D O}{O B}=1\n$$\n\nSince $D O=O B$ the above simplifies to $\\frac{B M}{C M}=\\frac{D N}{C N}$. It follows from $B M=B C+C M$ and $D N=D C-C N=A B-C N$ that the last equality is equivalent to:\n\n$$\n\\frac{B C}{C M}+2=\\frac{A B}{C N}\n$$\n\nDenote by $S$ the foot of the perpendicular from $B$ to $A C$. Since $\\Varangle B C S=\\Varangle C P M=\\varphi$ and $\\Varangle B A C=\\Varangle A C D=\\Varangle C P N=\\psi$ we conclude that $\\triangle C B S \\sim \\triangle P C M$ and $\\triangle A B S \\sim \\triangle P C N$. Therefore\n\n$$\n\\frac{C M}{B S}=\\frac{C P}{B C} \\text { and } \\frac{C N}{B S}=\\frac{C P}{A B}\n$$\n\nand thus,\n\n$$\nC M=\\frac{C P . B S}{B C} \\text { and } C N=\\frac{C P . B S}{A B}\n$$\n\nNow equality (1) becomes $A B^{2}-B C^{2}=2 C P . B S$. It follows from\n\n$$\nA B^{2}-B C^{2}=A S^{2}-C S^{2}=(A S-C S)(A S+C S)=2 O S . A C\n$$\n\nthat\n\n$$\nD C^{2}-B C^{2}=2 C P \\cdot B S \\Longleftrightarrow 2 O S \\cdot A C=2 C P . B S \\Longleftrightarrow O S \\cdot A C=C P \\cdot B S .\n$$\n\nSince $\\Varangle A C P=\\Varangle B S O=90^{\\circ}$ and $\\Varangle C A P=\\Varangle S B O$ we conclude that $\\triangle A C P \\sim \\triangle B S O$. This implies $O S . A C=C P . B S$, which completes the proof.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":50,"cells":{"problem":{"kind":"string","value":"\nG2. Let $A B C$ be an acute triangle such that $A B$ is the shortest side of the triangle. Let $D$ be the midpoint of the side $A B$ and $P$ be an interior point of the triangle such that\n\n$$\n\\Varangle C A P=\\Varangle C B P=\\Varangle A C B\n$$\n\nDenote by $M$ and $N$ the feet of the perpendiculars from $P$ to $B C$ and $A C$, respectively. Let $p$ be the line through $M$ parallel to $A C$ and $q$ be the line through $N$ parallel to $B C$. If $p$ and $q$ intersect at $K$ prove that $D$ is the circumcenter of triangle $M N K$.\n"},"solution":{"kind":"string","value":"\nSolution. If $\\gamma=\\Varangle A C B$ then $\\Varangle C A P=\\Varangle C B P=\\Varangle A C B=\\gamma$. Let $E=K N \\cap A P$ and $F=K M \\cap B P$. We show that points $E$ and $F$ are midpoints of $A P$ and $B P$, respectively.\n\n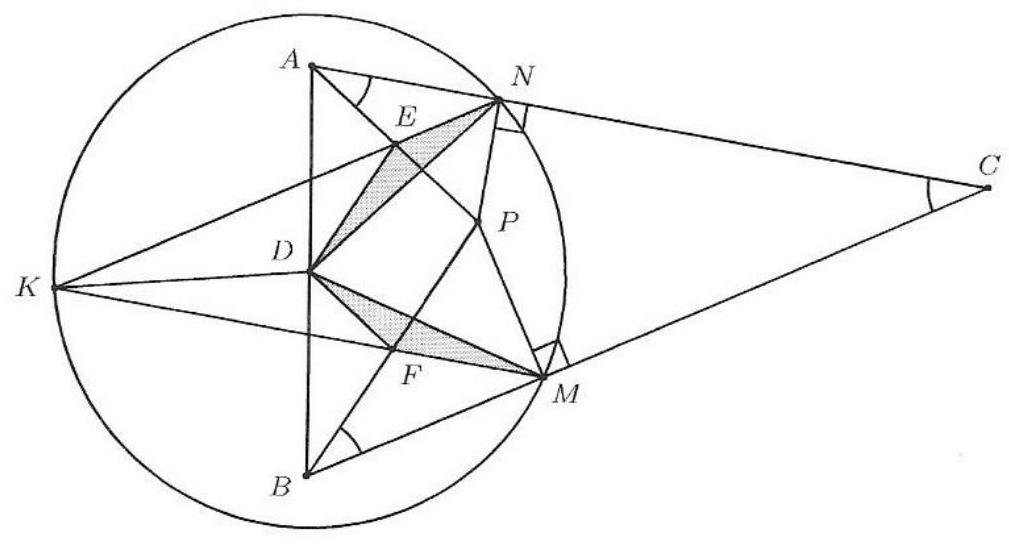![](https://cdn.mathpix.com/cropped/2024_06_05_7db2aacb858e7f253ee0g-13.jpg?height=545&width=1009&top_left_y=1137&top_left_x=539)\n\nIndeed, consider the triangle $A E N$. Since $K N \\| B C$, we have $\\Varangle E N A=\\Varangle B C A=\\gamma$. Moreover $\\Varangle E A N=\\gamma$ giving that triangle $A E N$ is isosceles, i.e. $A E=E N$. Next, consider the triangle $E N P$. Since $\\Varangle E N A=\\gamma$ we find that\n\n$$\n\\Varangle P N E=90^{\\circ}-\\Varangle E N A=90^{\\circ}-\\gamma\n$$\n\nNow $\\Varangle E P N=90^{\\circ}-\\gamma$ implies that the triangle $E N P$ is isosceles triangle, i.e. $E N=E P$.\n\nSince $A E=E N=E P$ point $E$ is the midpoint of $A P$ and analogously, $F$ is the midpoint of $B P$. Moreover, $D$ is also midpoint of $A B$ and we conclude that $D F P E$ is parallelogram.\n\nIt follows from $D E \\| A P$ and $K E \\| B C$ that $\\Varangle D E K=\\Varangle C B P=\\gamma$ and analogously $\\Varangle D F K=\\gamma$.\n\nWe conclude that $\\triangle E D N \\cong \\triangle F M D(E D=F P=F M, E N=E P=F D$ and $\\Varangle D E N=$ $\\left.\\Varangle M F D=180^{\\circ}-\\gamma\\right)$ and thus $N D=M D$. Therefore $D$ is a point on the perpendicular bisector of $M N$. Further,\n\n$$\n\\begin{aligned}\n\\Varangle F D E & =\\Varangle F P E=360^{\\circ}-\\Varangle B P M-\\Varangle M P N-\\Varangle N P A= \\\\\n& =360^{\\circ}-\\left(90^{\\circ}-\\gamma\\right)-\\left(180^{\\circ}-\\gamma\\right)-\\left(90^{\\circ}-\\gamma\\right)=3 \\gamma\n\\end{aligned}\n$$\n\nIt follows that\n\n$$\n\\begin{aligned}\n\\Varangle M D N & =\\Varangle F D E-\\Varangle F D M-\\Varangle E D N=\\Varangle F D E-\\Varangle E N D-\\Varangle E D N= \\\\\n& =\\Varangle F D E-(\\Varangle E N D+\\Varangle E D N)=3 \\gamma-\\gamma=2 \\gamma .\n\\end{aligned}\n$$\n\nFianlly, $K M C N$ is parallelogram, i.e. $\\Varangle M K N=\\Varangle M C N=\\gamma$. Therefore $D$ is a point on the perpendicular bisector of $M N$ and $\\Varangle M D N=2 \\Varangle M K N$, so $D$ is the circumcenter of $\\triangle M N K$.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":51,"cells":{"problem":{"kind":"string","value":"\nProblem G3. Consider triangle $A B C$ such that $A B \\leq A C$. Point $D$ on the arc $B C$ of the circumcirle of $A B C$ not containing point $A$ and point $E$ on side $B C$ are such that\n\n$$\n\\Varangle B A D=\\Varangle C A E<\\frac{1}{2} \\Varangle B A C .\n$$\n\nLet $S$ be the midpoint of segment $A D$. If $\\Varangle A D E=\\Varangle A B C-\\Varangle A C B$ prove that\n\n$$\n\\Varangle B S C=2 \\Varangle B A C\n$$\n"},"solution":{"kind":"string","value":"\nSolution. Let the tangent to the circumcircle of $\\triangle A B C$ at point $A$ intersect line $B C$ at $T$. Since $A B \\leq A C$ we get that $B$ lies between $T$ and $C$. Since $\\Varangle B A T=\\Varangle A C B$ and $\\Varangle A B T=\\Varangle 180^{\\circ}-\\Varangle A B C$ we get $\\Varangle E T A=\\Varangle B T A=\\Varangle A B C-\\Varangle A C B=\\Varangle A D E$ which gives that $A, E, D, T$ are concyclic. Since\n\n$$\n\\Varangle T D B+\\Varangle B C A=\\Varangle T D B+\\Varangle B D A=\\Varangle T D A=\\Varangle A E T=\\Varangle A C B+\\Varangle E A C\n$$\n\nthis means $\\Varangle T D B=\\Varangle E A C=\\Varangle D A B$ which means that $T D$ is tangent to the circumcircle of $\\triangle A B C$ at point $D$.\n\n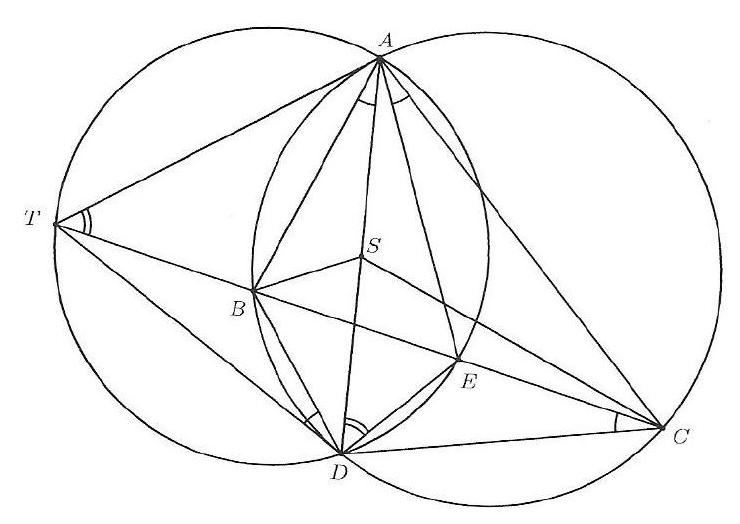![](https://cdn.mathpix.com/cropped/2024_06_05_7db2aacb858e7f253ee0g-15.jpg?height=524&width=740&top_left_y=1619&top_left_x=649)\n\nUsing similar triangles $T A B$ and $T C A$ we get\n\n$$\n\\frac{A B}{A C}=\\frac{T A}{T C}\n$$\n\nUsing similar triangles $T B D$ and $T D C$ we get\n\n$$\n\\frac{B D}{C D}=\\frac{T D}{T C}\n$$\n\nUsing the fact that $T A=T D$ with (1) and (2) we get\n\n$$\n\\frac{A B}{A C}=\\frac{B D}{C D}\n$$\n\nNow since $\\Varangle D A B=\\Varangle C A E$ and $\\Varangle B D A=\\Varangle E C A$ we get that the triangles $D A B$ and $C A E$ are similar. Analogously, we get that triangles $C A D$ and $E A B$ are similar. These similarities give us\n\n$$\n\\frac{D B}{C E}=\\frac{A B}{A E} \\quad \\text { and } \\quad \\frac{C D}{E B}=\\frac{C A}{E A}\n$$\n\nwhich, when combined with (3) give us $B E=C E$ giving $E$ is the midpoint of side $B C$.\n\nUsing the fact that triangles $D A B$ and $C A E$ are similar with the fact that $E$ is the midpoint of $B C$ we get:\n\n$$\n\\frac{2 D S}{C A}=\\frac{D A}{C A}=\\frac{D B}{C E}=\\frac{D B}{\\frac{C B}{2}}=\\frac{2 D B}{C B}\n$$\n\nimplying that\n\n$$\n\\frac{D S}{D B}=\\frac{C A}{C B}\n$$\n\nSince $\\Varangle S D B=\\Varangle A D B=\\Varangle A C B$ we get from (4) that the triangles $S D B$ and $A C B$ are similar, giving us $\\Varangle B S D=\\Varangle B A C$. Analogously we get $\\triangle S D C$ and $\\triangle A B C$ are similar we get $\\Varangle C S D=\\Varangle C A B$. Combining the last two equalities we get\n\n$$\n2 \\Varangle B A C=\\Varangle B A C+\\Varangle C A B=\\Varangle C S D+\\Varangle B S D=\\Varangle C S B\n$$\n\nThis completes the proof.\n\n"},"answer":{"kind":"string","value":"2\\VarangleBAC=\\VarangleBSC"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":52,"cells":{"problem":{"kind":"string","value":"\nProblem G4. Let $A B C$ be a scalene triangle with circumcircle $\\Gamma$ and circumcenter $O$. Let $M$ be the midpoint of $B C$ and $D$ be a point on $\\Gamma$ such that $A D \\perp B C$. Let $T$ be a point such that $B D C T$ is a parallelogram and $Q$ a point on the same side of $B C$ as $A$ such that\n\n$$\n\\Varangle B Q M=\\Varangle B C A \\quad \\text { and } \\quad \\Varangle C Q M=\\Varangle C B A\n$$\n\nLet $A O$ intersect $\\Gamma$ again at $E$ and let the circumcircle of $E T Q$ intersect $\\Gamma$ at point $X \\neq E$. Prove that the points $A, M$, and $X$ are collinear.\n"},"solution":{"kind":"string","value":"\nSolution. Let $X^{\\prime}$ be symmetric point to $Q$ in line $B C$. Now since $\\Varangle C B A=\\Varangle C Q M=$ $\\Varangle C X^{\\prime} M, \\Varangle B C A=\\Varangle B Q M=\\Varangle B X^{\\prime} M$, we have\n\n$$\n\\Varangle B X^{\\prime} C=\\Varangle B X^{\\prime} M+\\Varangle C X^{\\prime} M=\\Varangle C B A+\\Varangle B C A=180^{\\circ}-\\Varangle B A C\n$$\n\nwe have that $X^{\\prime} \\in \\Gamma$. Now since $\\Varangle A X^{\\prime} B=\\Varangle A C B=\\Varangle M X^{\\prime} B$ we have that $A, M, X^{\\prime}$ are collinear. Note that since\n\n$$\n\\Varangle D C B=\\Varangle D A B=90^{\\circ}-\\Varangle A B C=\\Varangle O A C=\\Varangle E A C\n$$\n\nwe get that $D B C E$ is an isosceles trapezoid.\n\n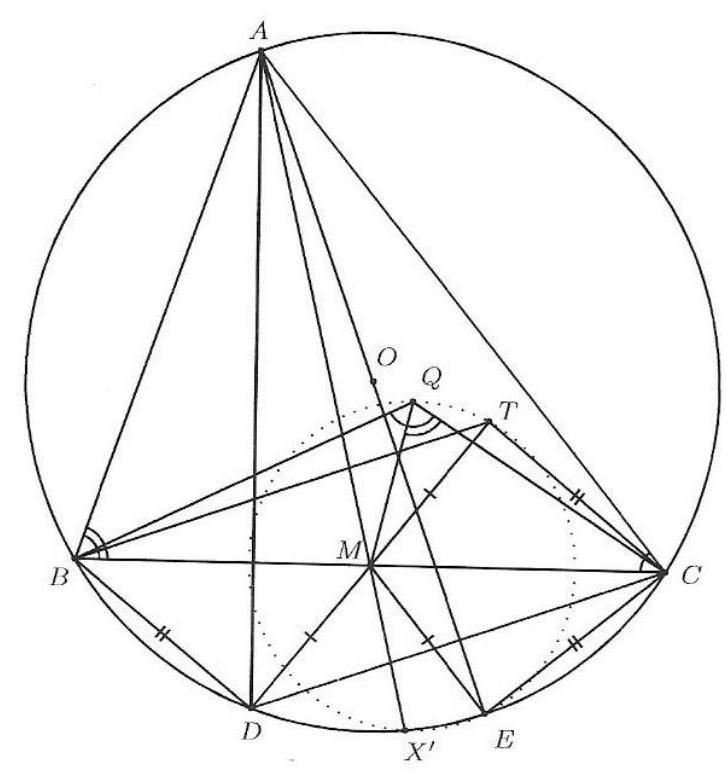![](https://cdn.mathpix.com/cropped/2024_06_05_7db2aacb858e7f253ee0g-18.jpg?height=772&width=727&top_left_y=1625&top_left_x=669)\n\nSince $B D C T$ is a parallelogram we have $M T=M D$, with $M, D, T$ being collinear, $B D=C T$, and since $B D E C$ is an isosceles trapezoid we have $B D=C E$ and $M E=M D$. Since\n\n$$\n\\Varangle B T C=\\Varangle B D C=\\Varangle B E D, \\quad C E=B D=C T \\quad \\text { and } \\quad M E=M T\n$$\n\nwe have that $E$ and $T$ are symmetric with respect to the line $B C$. Now since $Q$ and $X^{\\prime}$ are symmetric with respect to the line $B C$ as well, this means that $Q X^{\\prime} E T$ is an isosceles trapezoid which means that $Q, X^{\\prime}, E, T$ are concyclic. Since $X^{\\prime} \\in \\Gamma$ this means that $X \\equiv X^{\\prime}$ and therefore $A, M, X$ are collinear.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":53,"cells":{"problem":{"kind":"string","value":"\nProblem G5. A point $P$ lies in the interior of the triangle $A B C$. The lines $A P, B P$, and $C P$ intersect $B C, C A$, and $A B$ at points $D, E$, and $F$, respectively. Prove that if two of the quadrilaterals $A B D E, B C E F, C A F D, A E P F, B F P D$, and $C D P E$ are concyclic, then all six are concyclic.\n"},"solution":{"kind":"string","value":"\nSolution. We first prove the following lemma:\n\nLemma 1. Let $A B C D$ be a convex quadrilateral and let $A B \\cap C D=E$ and $B C \\cap D A=F$. Then the circumcircles of triangles $A B F, C D F, B C E$ and $D A E$ all pass through a common point $P$. This point lies on line $E F$ if and only if $A B C D$ in concyclic.\n\nProof. Let the circumcircles of $A B F$ and $B C F$ intersect at $P \\neq B$. We have\n\n$$\n\\begin{aligned}\n\\Varangle F P C & =\\Varangle F P B+\\Varangle B P C=\\Varangle B A D+\\Varangle B E C=\\Varangle E A D+\\Varangle A E D= \\\\\n& =180^{\\circ}-\\Varangle A D E=180^{\\circ}-\\Varangle F D C\n\\end{aligned}\n$$\n\nwhich gives us $F, P, C$ and $D$ are concyclic. Similarly we have\n\n$$\n\\begin{aligned}\n\\Varangle A P E & =\\Varangle A P B+\\Varangle B P E=\\Varangle A F B+\\Varangle B C D=\\Varangle D F C+\\Varangle F C D= \\\\\n& =180^{\\circ}-\\Varangle F D C=180^{\\circ}-\\Varangle A D E\n\\end{aligned}\n$$\n\nwhich gives us $E, P, A$ and $D$ are concyclic. Since $\\Varangle F P E=\\Varangle F P B+\\Varangle E P B=\\Varangle B A D+$ $\\Varangle B C D$ we get that $\\Varangle F P E=180^{\\circ}$ if and only if $\\Varangle B A D+\\Varangle B C D=180^{\\circ}$ which completes the lemma. We now divide the problem into cases:\n\nCase 1: $A E P F$ and $B F E C$ are concyclic. Here we get that\n\n$$\n180^{\\circ}=\\Varangle A E P+\\Varangle A F P=360^{\\circ}-\\Varangle C E B-\\Varangle B F C=360^{\\circ}-2 \\Varangle C E B\n$$\n\nand here we get that $\\Varangle C E B=\\Varangle C F B=90^{\\circ}$, from here it follows that $P$ is the ortocenter of $\\triangle A B C$ and that gives us $\\Varangle A D B=\\Varangle A D C=90^{\\circ}$. Now the quadrilaterals $C E P D$ and $B D P F$ are concyclic because\n\n$$\n\\Varangle C E P=\\Varangle C D P=\\Varangle P D B=\\Varangle P F B=90^{\\circ} .\n$$\n\nQuadrilaterals $A C D F$ and $A B D E$ are concyclic because\n\n$$\n\\Varangle A E B=\\Varangle A D B=\\Varangle A D C=\\Varangle A F C=90^{\\circ}\n$$\n\nCase 2: $A E P F$ and $C E P D$ are concyclic. Now by lemma 1 applied to the quadrilateral $A E P F$ we get that the circumcircles of $C E P, C A F, B P F$ and $B E A$ intersect at a point on $B C$. Since $D \\in B C$ and $C E P D$ is concyclic we get that $D$ is the desired point and it follows that $B D P F, B A E D, C A F D$ are all concylic and now we can finish same as Case 1 since $A E D B$ and $C E P D$ are concyclic.\n\nCase 3: $A E P F$ and $A E D B$ are concyclic. We apply lemma 1 as in Case 2 on the quadrilateral $A E P F$. From the lemma we get that $B D P F, C E P D$ and $C A F D$ are concylic and we finish off the same as in Case 1.\n\nCase 4: $A C D F$ and $A B D E$ are concyclic. We apply lemma 1 on the quadrilateral $A E P F$ and get that the circumcircles of $A C F, E C P, P F B$ and $B A E$ intersect at one point. Since this point is $D$ (because $A C D F$ and $A B D E$ are concyclic) we get that $A E P F, C E P D$ and $B F P D$ are concylic. We now finish off as in Case 1. These four cases prove the problem statement.\n\nRemark. A more natural approach is to solve each of the four cases by simple angle chasing.\n\n## Number Theory\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":54,"cells":{"problem":{"kind":"string","value":"\nNT1. Determine all sets of six consecutive positive integers such that the product of two of them, added to the the product of other two of them is equal to the product of the remaining two numbers.\n"},"solution":{"kind":"string","value":"\nSolution. Exactly two of the six numbers are multiples of 3 and these two need to be multiplied together, otherwise two of the three terms of the equality are multiples of 3 but the third one is not.\n\nLet $n$ and $n+3$ denote these multiples of 3 . Two of the four remaining numbers give remainder 1 when divided by 3 , while the other two give remainder 2 , so the two other products are either\n\n$\\equiv 1 \\cdot 1=1(\\bmod 3)$ and $\\equiv 2 \\cdot 2 \\equiv 1(\\bmod 3)$, or they are both $\\equiv 1 \\cdot 2 \\equiv 2(\\bmod 3)$. In conclusion, the term $n(n+3)$ needs to be on the right hand side of the equality.\n\nLooking at parity, three of the numbers are odd, and three are even. One of $n$ and $n+3$ is odd, the other even, so exactly two of the other numbers are odd. As $n(n+3)$ is even, the two remaining odd numbers need to appear in different terms.\n\nWe distinguish the following cases:\n\nI. The numbers are $n-2, n-1, n, n+1, n+2, n+3$.\n\nThe product of the two numbers on the RHS needs to be larger than $n(n+3)$. The only possibility is $(n-2)(n-1)+n(n+3)=(n+1)(n+2)$ which leads to $n=3$. Indeed, $1 \\cdot 2+3 \\cdot 6=4 \\cdot 5$\n\nII. The numbers are $n-1, n, n+1, n+2, n+3, n+4$.\n\nAs $(n+4)(n-1)+n(n+3)=(n+1)(n+2)$ has no solutions, $n+4$ needs to be on the RHS, multiplied with a number having a different parity, so $n-1$ or $n+1$.\n\n$(n+2)(n-1)+n(n+3)=(n+1)(n+4)$ leads to $n=3$. Indeed, $2 \\cdot 5+3 \\cdot 6=4 \\cdot 7$. $(n+2)(n+1)+n(n+3)=(n-1)(n+4)$ has no solution.\n\nIII. The numbers are $n, n+1, n+2, n+3, n+4, n+5$.\n\nWe need to consider the following situations:\n\n$(n+1)(n+2)+n(n+3)=(n+4)(n+5)$ which leads to $n=6$; indeed $7 \\cdot 8+6 \\cdot 9=10 \\cdot 11$;\n\n$(n+2)(n+5)+n(n+3)=(n+1)(n+4)$ obviously without solutions, and\n\n$(n+1)(n+4)+n(n+3)=(n+2)(n+5)$ which leads to $n=2$ (not a multiple of 3 ).\n\nIn conclusion, the problem has three solutions:\n\n$$\n1 \\cdot 2+3 \\cdot 6=4 \\cdot 5, \\quad 2 \\cdot 5+3 \\cdot 6=4 \\cdot 7, \\quad \\text { and } \\quad 7 \\cdot 8+6 \\cdot 9=10 \\cdot 11\n$$\n"},"answer":{"kind":"string","value":"1\\cdot2+3\\cdot6=4\\cdot5,\\quad2\\cdot5+3\\cdot6=4\\cdot7,\\quad7\\cdot8+6\\cdot9=10\\cdot11"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Incomplete"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":55,"cells":{"problem":{"kind":"string","value":"\nNT3. Find all pairs of positive integers $(x, y)$ such that $2^{x}+3^{y}$ is a perfect square.\n"},"solution":{"kind":"string","value":"\nSolution. In order for the expression $2^{x}+3^{y}$ to be a perfect square, a positive integer $t$ such that $2^{x}+3^{y}=t^{2}$ should exist.\n\nCase 1. If $x$ is even, then there exists a positive integer $z$ such that $x=2 z$. Then\n\n$$\n\\left(t-2^{z}\\right)\\left(t+2^{z}\\right)=3^{y}\n$$\n\nSince $t+2^{z}-\\left(t-2^{z}\\right)=2^{z+1}$, which implies $g c d\\left(t-2^{z}, t+2^{z}\\right) \\mid 2^{z+1}$, it follows that $\\operatorname{gcd}\\left(t-2^{z}, t+\\right.$ $\\left.2^{z}\\right)=1$, hence $t-2^{z}=1$ and $t+2^{z}=3^{y}$, so we have $2^{z+1}+1=3^{y}$.\n\nFor $z=1$ we have $5=3^{y}$ which clearly have no solution. For $z \\geq 2$ we have (modulo 4) that $y$ is even. Let $y=2 k$. Then $2^{z+1}=\\left(3^{k}-1\\right)\\left(3^{k}+1\\right)$ which is possible only when $3^{k}-1=2$, i.e. $k=1, y=2$, which implies that $t=5$. So the pair $(4,2)$ is a solution to our problem. Case 2. If $y$ is even, then there exists a positive integer $w$ such that $y=2 w$, and\n\n$$\n\\left(t-3^{w}\\right)\\left(t+3^{w}\\right)=2^{x}\n$$\n\nSince $t+3^{w}-\\left(t-3^{w}\\right)=2 \\cdot 3^{w}$, we have $\\operatorname{gcd}\\left(t-2^{z}, t+2^{z}\\right) \\mid 2 \\cdot 3^{w}$, which means that $g c d(t-$ $\\left.3^{w}, t+3^{w}\\right)=2$. Hence $t-3^{w}=2$ and $t+3^{w}=2^{x-1}$. So we have\n\n$$\n2 \\cdot 3^{w}+2=2^{x-1} \\Rightarrow 3^{w}+1=2^{x-2}\n$$\n\nHere we see modulo 3 that $x-2$ is even. Let $x-2=2 m$, then $3^{w}=\\left(2^{m}-1\\right)\\left(2^{m}+1\\right)$, whence $m=1$ since $\\operatorname{gcd}\\left(2^{m}-1,2^{m}+1\\right)=1$. So we arrive again to the solution $(4,2)$.\n\nCase 3. Let $x$ and $y$ be odd. For $x \\geq 3$ we have $2^{x}+3^{y} \\equiv 3(\\bmod 4)$ while $t^{2} \\equiv 0,1(\\bmod 4)$, a contradiction. For $x=1$ we have $2+3^{y}=t^{2}$. For $y \\geq 2$ we have $2+3^{y} \\equiv 2(\\bmod 9)$ while $t^{2} \\equiv 0,1,4,7(\\bmod 9)$. For $y=1$ we have $5=2+3=t^{2}$ clearly this doesn't have solution. Note. The proposer's solution used Zsigmondy's theorem in the final steps of cases 1 and 2 .\n"},"answer":{"kind":"string","value":"(4,2)"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":56,"cells":{"problem":{"kind":"string","value":"\nNT4. Solve in nonnegative integers the equation $5^{t}+3^{x} 4^{y}=z^{2}$.\n"},"solution":{"kind":"string","value":"\nSolution. If $x=0$ we have\n\n$$\nz^{2}-2^{2 y}=5^{t} \\Longleftrightarrow\\left(z+2^{y}\\right)\\left(z-2^{y}\\right)=5^{t}\n$$\n\nPutting $z+2^{y}=5^{a}$ and $z-2^{y}=5^{b}$ with $a+b=t$ we get $5^{a}-5^{b}=2^{y+1}$. This gives us $b=0$ and now we have $5^{t}-1=2^{y+1}$. If $y \\geq 2$ then consideration by modulo 8 gives $2 \\mid t$. Putting $t=2 s$ we get $\\left(5^{s}-1\\right)\\left(5^{s}+1\\right)=2^{y+1}$. This means $5^{s}-1=2^{c}$ and $5^{s}+1=2^{d}$ with $c+d=y+1$. Subtracting we get $2=2^{d}-2^{c}$. Then we have $c=1, d=2$, but the equation $5^{s}-1=2$ has no solutions over nonnegative integers. Therefore so $y \\geq 2$ in this case gives us no solutions. If $y=0$ we get again $5^{t}-1=2$ which again has no solutions in nonnegative integers. If $y=1$ we get $t=1$ and $z=3$ which gives us the solution $(t, x, y, z)=(1,0,1,3)$.\n\nNow if $x \\geq 1$ then by modulo 3 we have $2 \\mid t$. Putting $t=2 s$ we get\n\n$$\n3^{x} 4^{y}=z^{2}-5^{2 s} \\Longleftrightarrow 3^{x} 4^{y}=\\left(z+5^{s}\\right)\\left(z-5^{s}\\right)\n$$\n\nNow we have $z+5^{s}=3^{m} 2^{k}$ and $z-5^{s}=3^{n} 2^{l}$, with $k+l=2 y$ and $m+n=x \\geq 1$. Subtracting we get\n\n$$\n2.5^{s}=3^{m} 2^{k}-3^{n} 2^{l}\n$$\n\nHere we get that $\\min \\{m, n\\}=0$. We now have a couple of cases.\n\nCase 1. $k=l=0$. Now we have $n=0$ and we get the equation $2.5^{s}=3^{m}-1$. From modulo 4 we get that $m$ is odd. If $s \\geq 1$ we get modulo 5 that $4 \\mid m$, a contradiction. So $s=0$ and we get $m=1$. This gives us $t=0, x=1, y=0, z=2$.\n\nCase 2. $\\min \\{k, l\\}=1$. Now we deal with two subcases:\n\nCase 2a. $l>k=1$. We get $5^{s}=3^{m}-3^{n} 2^{l-1}$. Since $\\min \\{m, n\\}=0$, we get that $n=0$. Now the equation becomes $5^{s}=3^{m}-2^{l-1}$. Note that $l-1=2 y-2$ is even. By modulo 3 we get that $s$ is odd and this means $s \\geq 1$. Now by modulo 5 we get $3^{m} \\equiv 2^{2 y-2} \\equiv 1,-1(\\bmod 5)$. Here we get that $m$ is even as well, so we write $m=2 q$. Now we get $5^{s}=\\left(3^{q}-2^{y-1}\\right)\\left(3^{q}+2^{y-1}\\right)$.\n\nTherefore $3^{q}-2^{y-1}=5^{v}$ and $3^{q}+2^{y-1}=5^{u}$ with $u+v=s$. Then $2^{y}=5^{u}-5^{v}$, whence $v=0$ and we have $3^{q}-2^{y-1}=1$. Plugging in $y=1,2$ we get the solution $y=2, q=1$. This gives us $m=2, s=1, n=0, x=2, t=2$ and therefore $z=13$. Thus we have the solution $(t, x, y, z)=(2,2,2,13)$. If $y \\geq 3$ we get modulo 4 that $q, q=2 r$. Then $\\left(3^{r}-1\\right)\\left(3^{r}+1\\right)=2^{y-1}$. Putting $3^{r}-1=2^{e}$ and $3^{r}+1=2^{f}$ with $e+f=y-1$ and subtracting these two and dividing by 2 we get $2^{f-1}-2^{e-1}=1$, whence $e=1, f=2$. Therefore $r=1, q=2, y=4$. Now since $2^{4}=5^{u}-1$ does not have a solution, it follows that there are no more solutions in this case.\n\nCase $2 b . \\quad k>l=1$. We now get $5^{s}=3^{m} 2^{k-1}-3^{n}$. By modulo 4 (which we can use since $0<k-1=2 y-2)$ we get $3^{n} \\equiv-1(\\bmod 4)$ and therefore $n$ is odd. Now since $\\min \\{m, n\\}=0$ we get that $m=0,0+n=m+n=x \\geq 1$. The equation becomes $5^{s}=2^{2 y-2}-3^{x}$. By modulo 3 we see that $s$ is even. We now put $s=2 g$ and obtain $\\left(2^{y-1}-5^{g}\\right)\\left(5^{g}+2^{y-1}\\right)=3^{x}$. Putting $2^{y-1}-5^{g}=3^{h}, 2^{y-1}+5^{g}=3^{i}$, where $i+h=x$, and subtracting the equations we get $3^{i}-3^{h}=2^{y}$. This gives us $h=0$ and now we are solving the equation $3^{x}+1=2^{y}$.\n\nThe solution $x=0, y=1$ gives $1-5^{g}=1$ without solution. If $x \\geq 1$ then by modulo 3 we get that $y$ is even. Putting $y=2 y_{1}$ we obtain $3^{x}=\\left(2^{y_{1}}-1\\right)\\left(2^{y_{1}}+1\\right)$. Putting $2^{y_{1}}-1=3^{x_{1}}$ and $2^{y_{1}}+1=3^{x_{2}}$ and subtracting we get $3^{x_{2}}-3^{x_{1}}=2$. This equation gives us $x_{1}=0, x_{2}=1$. Then $y_{1}=1, x=1, y=2$ is the only solution to $3^{x}+1=2^{y}$ with $x \\geq 1$. Now from $2-5^{g}=1$ we get $g=0$. This gives us $t=0$. Now this gives us the solution $1+3.16=49$ and $(t, x, y, z)=(0,1,2,7)$.\n\nThis completes all the cases and thus the solutions are $(t, x, y, z)=(1,0,1,3),(0,1,0,2)$, $(2,2,2,13)$, and $(0,1,2,7)$.\n\nNote. The problem can be simplified by asking for solutions in positive integers (without significant loss in ideas).\n"},"answer":{"kind":"string","value":"(,x,y,z)=(1,0,1,3),(0,1,0,2),(2,2,2,13),(0,1,2,7)"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":57,"cells":{"problem":{"kind":"string","value":"\nNT5. Find all positive integers $n$ such that there exists a prime number $p$, such that\n\n$$\np^{n}-(p-1)^{n}\n$$\n\nis a power of 3 .\n\nNote. A power of 3 is a number of the form $3^{a}$ where $a$ is a positive integer.\n"},"solution":{"kind":"string","value":"\nSolution. Suppose that the positive integer $n$ is such that\n\n$$\np^{n}-(p-1)^{n}=3^{a}\n$$\n\nfor some prime $p$ and positive integer $a$.\n\nIf $p=2$, then $2^{n}-1=3^{a}$ by $(1)$, whence $(-1)^{n}-1 \\equiv 0(\\bmod 3)$, so $n$ should be even. Setting $n=2 s$ we obtain $\\left(2^{s}-1\\right)\\left(2^{s}+1\\right)=3^{a}$. It follows that $2^{s}-1$ and $2^{s}+1$ are both powers of 3 , but since they are both odd, they are co-prime, and we have $2^{s}-1=1$, i.e. $s=1$ and $n=2$. If $p=3$, then (1) gives $3 \\mid 2^{n}$, which is impossible.\n\nLet $p \\geq 5$. Then it follows from (1) that we can not have $3 \\mid p-1$. This means that $2^{n}-1 \\equiv 0$ $(\\bmod 3)$, so $n$ should be even, and let $n=2 k$. Then\n\n$$\np^{2 k}-(p-1)^{2 k}=3^{a} \\Longleftrightarrow\\left(p^{k}-(p-1)^{k}\\right)\\left(p^{k}+(p-1)^{k}\\right)=3^{a}\n$$\n\nIf $d=\\left(p^{k}-(p-1)^{k}, p^{k}+(p-1)^{k}\\right)$, then $d \\mid 2 p^{k}$. However, both numbers are powers of 3 , so $d=1$ and $p^{k}-(p-1)^{k}=1, p^{k}+(p-1)^{k}=3^{a}$.\n\nIf $k=1$, then $n=2$ and we can take $p=5$. For $k \\geq 2$ we have $1=p^{k}-(p-1)^{k} \\geq p^{2}-(p-1)^{2}$ (this inequality is equivalent to $p^{2}\\left(p^{k-2}-1\\right) \\geq(p-1)^{2}\\left((p-1)^{k-2}-1\\right)$, which is obviously true). Then $1 \\geq p^{2}-(p-1)^{2}=2 p-1 \\geq 9$, which is absurd.\n\nIt follows that the only solution is $n=2$.\n\n"},"answer":{"kind":"string","value":"2"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":58,"cells":{"problem":{"kind":"string","value":"\nA2. Let $a, b, c$ be positive real numbers such that abc $=1$. Show that\n\n$$\n\\frac{1}{a^{3}+b c}+\\frac{1}{b^{3}+c a}+\\frac{1}{c^{3}+a b} \\leq \\frac{(a b+b c+c a)^{2}}{6}\n$$\n\nso\n"},"solution":{"kind":"string","value":"\nSolution. By the AM-GM inequality we have $a^{3}+b c \\geq 2 \\sqrt{a^{3} b c}=2 \\sqrt{a^{2}(a b c)}=2 a$ and\n\n$$\n\\frac{1}{a^{3}+b c} \\leq \\frac{1}{2 a}\n$$\n\nSimilarly; $\\frac{1}{b^{3}+c a} \\leq \\frac{1}{2 b} \\cdot \\frac{1}{c^{3}+a b} \\leq \\frac{1}{2 c}$ and then\n\n$$\n\\frac{1}{a^{3}+b c}+\\frac{1}{b^{3}+c a}+\\frac{1}{c^{3}+a b} \\leq \\frac{1}{2 a}+\\frac{1}{2 b}+\\frac{1}{2 c}=\\frac{1}{2} \\frac{a b+b c+c a}{a b c} \\leq \\frac{(a b+b c+c a)^{2}}{6}\n$$\n\nTherefore it is enongil to prove $\\frac{(a h+b c+c a)^{2}}{6} \\leq \\frac{(a b+b c+c a)^{2}}{6}$. This mequalits is trivially shomn to be equivalent to $3 \\leq a b+b c+c a$ which is true because of the AM-GM inequalit: $3=\\sqrt[3]{(a b c)^{2}} \\leq a b+b c+c a$.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":59,"cells":{"problem":{"kind":"string","value":"\nA3. Let $a . b$ c ce positue real numbers such that $a+b+c=a^{2}+b^{2}+c^{2}$. Shou that\n\n$$\n\\frac{a^{2}}{a^{2}+a b}+\\frac{b^{2}}{b^{2}+b c}+\\frac{c^{2}}{c^{2}+c a} \\geq \\frac{a+b+c}{2}\n$$\n"},"solution":{"kind":"string","value":"\nSolution. By the Cauchy-Schwarz inequality it is\n\n$$\n\\begin{aligned}\n& \\left(\\frac{a^{2}}{a^{2}+a b}+\\frac{b^{2}}{b^{2}+b c}+\\frac{c^{2}}{c^{2}+c a}\\right)\\left(\\left(a^{2}+a b\\right)+\\left(b^{2}+b c\\right)+\\left(c^{2}+c a\\right)\\right) \\geq(a+b+c)^{2} \\\\\n\\Rightarrow & \\frac{a^{2}}{a^{2}+a b}+\\frac{b^{2}}{b^{2}+b c}+\\frac{c^{2}}{c^{2}+c a} \\geq \\frac{(a+b+c)^{2}}{a^{2}+b^{2}+c^{2}+a b+b c+c a}\n\\end{aligned}\n$$\n\nSo in is enough to prove $\\frac{(a+b+c)^{2}}{a^{2}+b^{2}+c^{2}+a b+b c+c a} \\geq \\frac{a+b+c}{2}$, that is to prove\n\n$$\n2(a+b+c) \\geq a^{2}+b^{2}+c^{2}+a b+b c+c a\n$$\n\nSubstituting $a^{2}+b^{2}+c^{2}$ for $a+b+c$ into the left hand side we wish equivalently to prove\n\n$$\na^{2}+b^{2}+c^{2} \\geq a b+b c+c a\n$$\n\nBut the $a^{2}+b^{2} \\geq 2 a b, b^{2}+c^{2} \\geq 2 b c, c^{2}+a^{2} \\geq 2 c a$ which by addition imply the desired inequality.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":60,"cells":{"problem":{"kind":"string","value":"\nA4. Solve the following equation for $x, y, z \\in \\mathbb{N}$\n\n$$\n\\left(1+\\frac{x}{y+z}\\right)^{2}+\\left(1+\\frac{y}{z+x}\\right)^{2}+\\left(1+\\frac{z}{x+y}\\right)^{2}=\\frac{27}{4}\n$$\n"},"solution":{"kind":"string","value":"\nSolution 1. Call $a=1+\\frac{x}{y+z}, b=1+\\frac{y}{z+x}, c=1+\\frac{z}{x+y}$ to get\n\n$$\na^{2}+b^{2}+c^{2}=\\frac{27}{4}\n$$\n\nSince it is also true that\n\n$$\n\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}=2\n$$\n\nthe quadratic-harmonic means inequality implies\n\n$$\n\\frac{3}{2}=\\sqrt{\\frac{a^{2}+b^{2}+c^{2}}{3}} \\geq \\frac{3}{\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}}=\\frac{3}{2}\n$$\n\nSo the inequality in the middle holds as an equality, and this happens whenever $a=b=c$, from which $1+\\frac{x}{y+z}=1+\\frac{y}{z+x}=1+\\frac{z}{x+y}$.\n\nBut $1+\\frac{x}{y+z}=1+\\frac{y}{z+x} \\Leftrightarrow x^{2}+x z=y^{2}+y z \\Leftrightarrow(x-y)(x+y)=z(y-\\dot{x})$ and the two sides of this equality will be of different sign, unless $x=y$ in which case both sides become 0 . So $x=y$, and similarly $y=z$, thus $x=y=z$.\n\nIndeed, any triad of equal natural numbers $x=y=z$ is a solution for the given equation, and so these are all its solutions.\n"},"answer":{"kind":"string","value":"z"},"problem_type":{"kind":"string","value":"Algebra"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":61,"cells":{"problem":{"kind":"string","value":"\nA5. Find the largest positive integer $n$ for which the inequality\n\n$$\n\\frac{a+b+c}{a b c+1}+\\sqrt[n]{a b c} \\leq \\frac{5}{2}\n$$\n\nholds for all $a, b, c \\in[0,1]$. Here $\\sqrt[1]{a b c}=a b c$.\n"},"solution":{"kind":"string","value":"\nSolution. Let $n_{\\max }$ be the sought largest value of $n$, and let $E_{a, b, c}(n)=\\frac{a+b+c}{a b c+1}+\\sqrt[n]{a b c}$. Then $E_{a, b, c}(m)-E_{a, b, c}(n)=\\sqrt[m]{a b c}-\\sqrt[n]{a b c}$ and since $a . b c \\leq 1$ we clearly have $E_{a, b, c}(m) \\geq$ $E_{a, b, c}(n)$ for $m \\geq n$. So if $E_{a, b, c}(n) \\geq \\frac{5}{2}$ for some choice of $a, b, c \\in[0,1]$, it must be $n_{\\max } \\leq n$. We use this remark to determine the upper bound $n_{\\max } \\leq 3$ by plugging some particular values of $a, b, c$ into the given inequality as follow's:\n\n$$\n\\text { For }(a, b, c)=(1,1, c), c \\in[0,1] \\text {, inequality (1) implies } \\frac{c+2}{c+1}+\\sqrt[n]{c} \\leq \\frac{5}{2} \\Leftrightarrow \\frac{1}{c+1}+\\sqrt[n]{c} \\leq\n$$\n\n$\\frac{3}{2}$. Obviously, every $x \\in[0 ; 1]$ is written as $\\sqrt[n]{c}$ for some $c \\in[0 ; 1]$. So the last inequality is equivalent to:\n\n$$\n\\begin{aligned}\n& \\frac{1}{x^{n}+1}+x \\leq \\frac{3}{2} \\Leftrightarrow 2+2 x^{n+1}+2 x \\leq 3 x^{n}+3 \\Leftrightarrow 3 x^{n}+1 \\geq 2 x^{n+1}+2 x \\\\\n\\Leftrightarrow & 2 x^{n}(1-x)+(1-x)+(x-1)\\left(x^{n-1}+\\cdots+x\\right) \\geq 0 \\\\\n\\Leftrightarrow & (1-x)\\left[2 x^{n}+1-\\left(x^{n-1}+x^{n-2}+\\ldots+x\\right)\\right] \\geq 0, \\forall x \\in[0,1]\n\\end{aligned}\n$$\n\nFor $n=4$, the left hand side of the above becomes $(1-x)\\left(2 x^{4}+1-x^{3}-x^{2}-x\\right)=$ $(1-x)(x-1)\\left(2 x^{3}+x^{2}-1\\right)=-(1-x)^{2}\\left(2 x^{3}+x^{2}-1\\right)$ which for $x=0.9$ is negative. Thus. $n_{\\max } \\leq 3$ as claimed.\n\nNow, we shall prove that for $n=3$ inequality (1) holds for all $a, b, c \\in[0,1]$, and this would mean $n_{\\max }=3$. We shall use the following Lemma:\n\nLemma. For all $a, b, c \\in[0 ; 1]: a+b+c \\leq a b c+2$.\nProof of the Lemma: The required result comes by adding the following two inequalities side by side\n\n$$\n\\begin{aligned}\n& 0 \\leq(a-1)(b-1) \\Leftrightarrow a+b \\leq a b+1 \\Leftrightarrow a+b-a b \\leq 1 \\\\\n& 0 \\leq(a b-1)(c-1) \\Leftrightarrow a b+c \\leq a b c+1\n\\end{aligned}\n$$\n\nBecause of the Lemma, our inequality (1) for $n=3$ wrill be proved if the following weaker inequality is proved for all $a, b, c \\in[0,1]$ :\n\n$$\n\\frac{a b c+2}{a b c+1}+\\sqrt[3]{a b c} \\leq \\frac{5}{2} \\Leftrightarrow \\frac{1}{a b c+1}+\\sqrt[3]{a b c} \\leq \\frac{3}{2}\n$$\n\nDenoting $\\sqrt[3]{a b c}=y \\in[0 ; 1]$, this inequality becomes:\n\n$$\n\\begin{aligned}\n& \\frac{1}{y^{3}+1}+y \\leq \\frac{3}{2} \\Leftrightarrow 2+2 y^{4}+2 y \\leq 3 y^{3}+3 \\Leftrightarrow-2 y^{4}+3 y^{3}-2 y+1 \\geq 0 \\\\\n\\Leftrightarrow & 2 y^{3}(1-y)+(y-1) y(y+1)+(1-y) \\geq 0 \\Leftrightarrow(1-y)\\left(2 y^{3}+1-y^{2}-y\\right) \\geq 0\n\\end{aligned}\n$$\n\nThe last inequality is obvious because $1-y \\geq 0$ and $2 y^{3}+1-y^{2}-y=y^{3}+(y-1)^{2}(y+1) \\geq 0$.\n\n## Geometry\n\n2\n"},"answer":{"kind":"string","value":"3"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":62,"cells":{"problem":{"kind":"string","value":"\nG1. Let $A B C$ be an equilateral triangle, and $P$ a point on the circumcircle of the triangle $A B C$ and distinct from $A, B$ and $C$. If the lines through $P$ and parallel to $B C, C A, A B$ intersect the lines $C A, A B, B C$ at $M, N$ and $Q$ respectively, prove that $M, N$ and $Q$ are collinear.\n"},"solution":{"kind":"string","value":"\nSolution. Without any loss of generality, let $P$ be in the minor arc of the chord $A C$ as in Figure 1. Since $\\angle P N A=\\angle N P M=60^{\\circ}$ and $\\angle N A M=\\angle P M A=120^{\\circ}$, it follows that the points $A, M, P$ and $N$ are concyclic. This yields\n\n$$\n\\angle N M P=\\angle N A P\n$$\n\n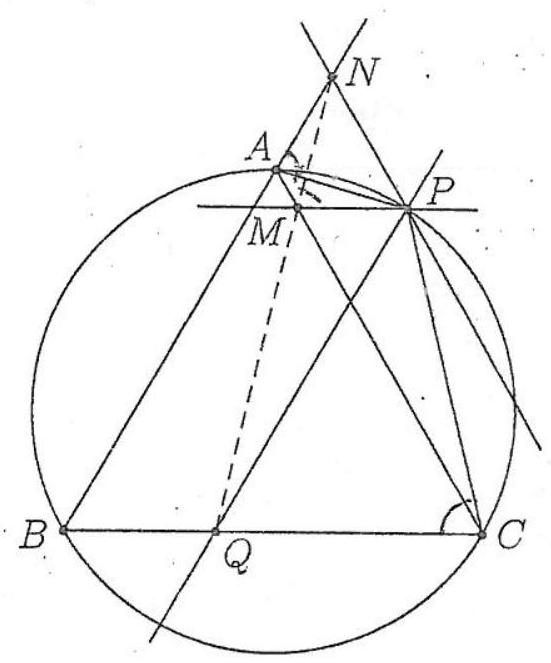![](https://cdn.mathpix.com/cropped/2024_06_05_61d3145f18c90bf9f370g-05.jpg?height=663&width=551&top_left_y=933&top_left_x=795)\n\nFigure 1: Exercise G1.\n\nSimilarly, since $\\angle P M C=\\angle M C Q=60^{\\circ}$ and $\\angle C Q P=60^{\\circ}$, it follows that the points $P, M, Q$ and $C$ are concyclic. Thus\n\n$$\n\\angle P M Q=180^{\\circ}-\\angle P C Q=180^{\\circ}-\\angle N A P \\stackrel{(2)}{=} 180^{\\circ}-\\angle N M P .\n$$\n\nThis implies $\\angle P M Q+\\angle N M P=180^{\\circ}$, which shows that $M, N$ and $Q$ belong to the same line.\n\n1 G2. Let $A B C$ be an isosceles triangle with $A B=A C$. Let also $c(K, K C)$ be a circle tangent to the line $A C$ at point $C$ which it intersects the segment $B C$ again at an interior point $H$. Prove that $H K \\perp A B$.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":63,"cells":{"problem":{"kind":"string","value":"\nG4. Let $A B C$ be an acute-angled triangle with circumcircle $\\Gamma$, and let $O, H$ be the triangle's circumcenter and orthocenter respectively. Let also $A^{\\prime}$ be the point where the angle bisector of angle $B A C$ meets $\\Gamma$. If $A^{\\prime} H=A H$, find the measure of angle $B A C$.\n\n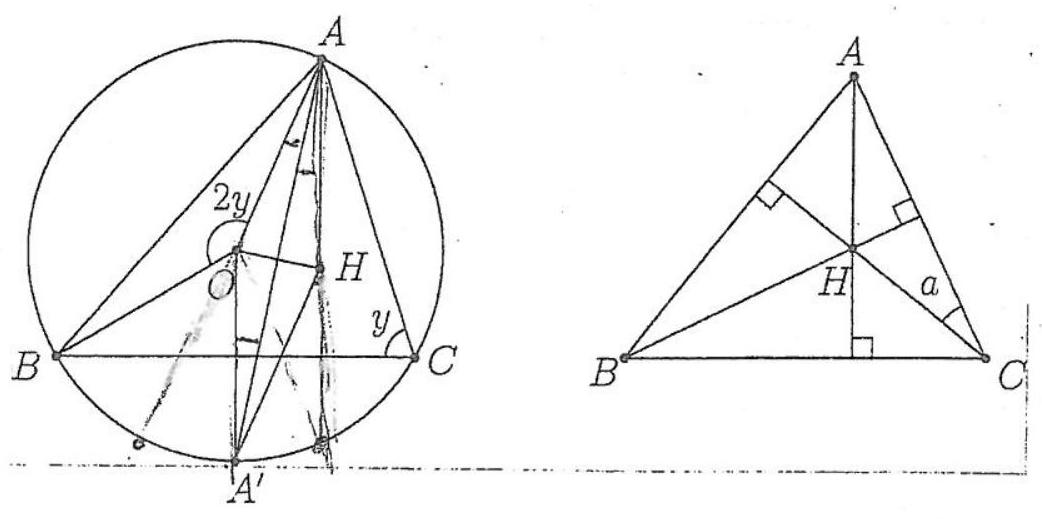![](https://cdn.mathpix.com/cropped/2024_06_05_61d3145f18c90bf9f370g-07.jpg?height=519&width=1042&top_left_y=1756&top_left_x=541)\n\nFigure 4: Exercise G4.\n"},"solution":{"kind":"string","value":"\nSolution. The segment $A A^{\\prime}$ bisects $\\angle O A H$ : if $\\angle B C A=y$ (Figure 4), then $\\angle B O A=$ $2 y$, and since $O A=O B$, it is $\\angle O A B=\\angle O B A=90^{\\circ}-y$. Also since $A H \\perp B C$, it is\n$\\angle H A C=90^{\\circ}-y=\\angle O A B$ and the claim follows.\n\nSince $A . A^{\\prime}$ bisects $\\angle O A H$ and $A^{\\prime} H=A H . O A^{\\prime}=O A$, we have that the isosceles triangles $O A A^{\\prime}, H A A^{\\prime}$ are equal. Thus\n\n$$\nA H=O A=R\n$$\n\nwhere $R$ is the circumradius of triangle $A B C$.\n\nCall $\\angle A C H=a$ and recall by the law of sines that $A H=2 R^{\\prime} \\sin a$, where $R^{\\prime}$ is the circumradius of triangle $A H C$. Then (4) implies\n\n$$\nR=2 R^{\\prime} \\sin a\n$$\n\nBut notice that $R=R^{\\prime}$ because $\\frac{A C}{\\sin (A H C)}=2 R^{\\prime}, \\frac{A C}{\\sin (A B C)}=2 R$ and $\\sin (A H C)=$ $\\sin \\left(180^{\\circ}-A B C\\right)=\\sin (A B C)$. So (5) gives $1=2 \\sin a$, and $a$ as an acuite angle can only be $30^{\\circ}$. Finally, $\\angle B A C=90^{\\circ}-a=60^{\\circ}$.\n\nRemark. The steps in the above proof can be traced backwards making the converse also true, that is: If $\\angle B A C=60^{\\circ}$ then $A^{\\prime} H=A H$.\n\n- G5. Let the circles $k_{1}$ and $k_{2}$ intersect at two distinct points $A$ and $B$, and let $t$ be a common tangent of $k_{1}$ and $k_{2}$ that touches them at $M$ and, $N$ respectively. If $t \\perp A M$ and $M N=2 A M$, evaluate $\\angle N M B$.\n\n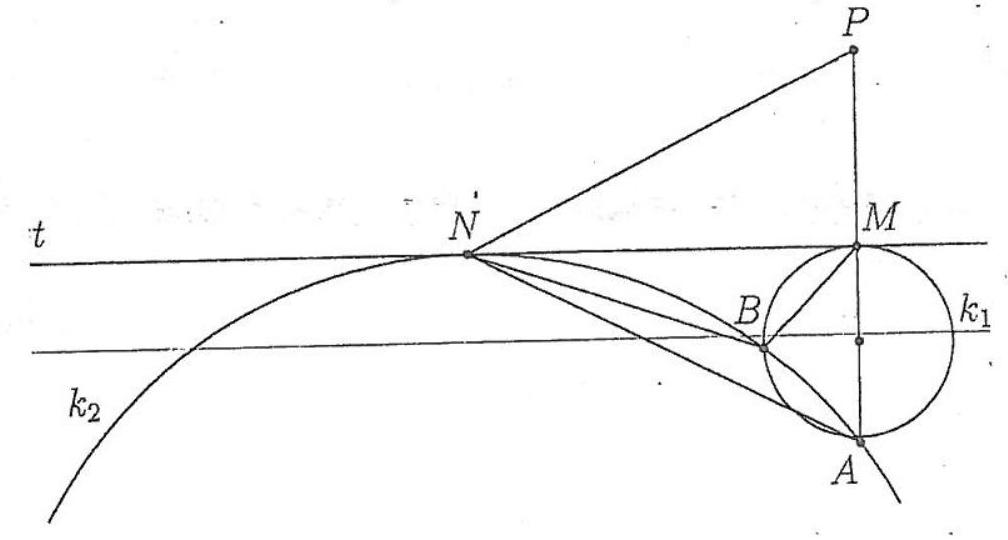![](https://cdn.mathpix.com/cropped/2024_06_05_61d3145f18c90bf9f370g-08.jpg?height=540&width=1008&top_left_y=1454&top_left_x=589)\n\nFigure 5: Exercise G5.\n"},"answer":{"kind":"string","value":"60"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":64,"cells":{"problem":{"kind":"string","value":"\nC1. Along a round table are arranged 11 cards with the names (all distinct) of the 11 members of the $16^{\\text {th }}$ JBMO Problem Selection Committee. The distances between each two consecutive cards are equal. Assume that in the first meeting of the Committee none of its 11 members sits in front of the card with his name. Is it possible to rotate the table by some angle so that at the end at least two members of sit in front of the card with their names?\n"},"solution":{"kind":"string","value":"\nSolution. Yes it is: Rotating the table by the angles $\\frac{360^{\\circ}}{11}, 2 \\cdot \\frac{360^{\\circ}}{11}, 3 \\cdot \\frac{360^{\\circ}}{11}, \\ldots, 10 \\cdot \\frac{360^{\\circ}}{11}$, we obtain 10 new positions of the table. By the assumption, it is obvious that every one of the 11 members of the Committee will be seated in front of the card with his name in exactly one of these 10 positions. Then by the Pigeonhole Principle there should exist one among these 10 positions in which at least two of the $11(>10)$ members of the Committee will be placed in their positions, as claimed.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":65,"cells":{"problem":{"kind":"string","value":"\nC2. $n$ nails nailed on a board are connected by two via a string. Each string is colored in one of $n$ given colors. For any three colors there exist three nails conne.cted by two with strings in these three colors. Can $n$ be: (a) 6, (b) 7?\n"},"solution":{"kind":"string","value":"\nSolution. (a) The answer is no:\n\nSuppose it is possible. Consider some color, say blue. Each blue string is the side of 4 triangles formed with vertices on the given points. As there exist $\\binom{5}{2}=\\frac{5 \\cdot 4}{2}=10$ pairs of colors other than blue, and for any such pair of colors together with the blue color there exists a triangle with strings in these colors, we conclude that there exist at least 3 blue strings (otherwise the number of triangles with a blue string as a side would be at most $2 \\cdot 4=8$, a contradiction). The same is true for any color, so altogether there exist at least $6 \\cdot 3=18$ strings, while we have just $\\binom{6}{2}=\\frac{6 \\cdot 5}{2}=15$ of them.\n\n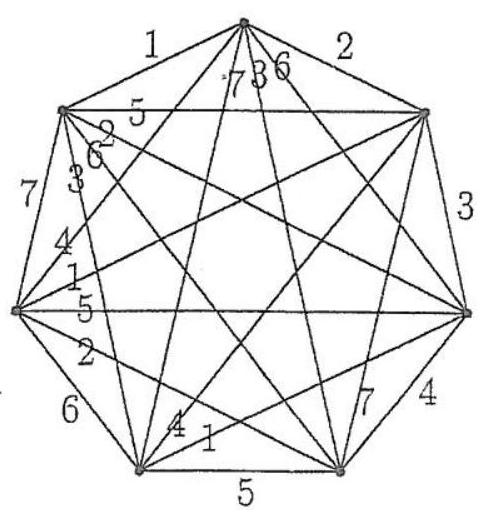![](https://cdn.mathpix.com/cropped/2024_06_05_61d3145f18c90bf9f370g-12.jpg?height=519&width=488&top_left_y=1850&top_left_x=835)\n\nFigure 8: Exercise C2.\n\n(b) The answer is yes (Figure 8):\n\nPut the nails at the vertices of a regular 7-gon (Figure 8) and color each one of its sides in a different color. Now color each diagonal in the color of the unique side parallel to it. It can be checked directly that each triple of colors appears in some triangle (because of symmetry, it is enough to check only the triples containing the first color).\n\nRemark. The argument in (a) can be applied to any even $n$. The argument. in (b) can be applied to any odd $n=2 k+1$ as follows: first number the nails as $0,1,2 \\ldots, 2 k$ and similarly number the colors as $0,1,2 \\ldots, 2 k$. Then connect nail $x$ with nail $y$ by a string of color $x+y(\\bmod n)$. For each triple of colors $(p, q, r)$ there are vertices $x, y, z$ connected by these three colors. Indeed, we need to solve (modn.) the system\n\n$$\n(*)(x+y \\equiv p, x+z \\equiv q, y+z \\equiv r)\n$$\n\nAdding all three, we get $2(x+y+z) \\equiv p+q+r$ and multiplying by $k+1$ we get $x+y+z \\equiv$ $(k+1)(p+q+r)$. We can now find $x, y, z$ from the identities $(*)$.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":66,"cells":{"problem":{"kind":"string","value":"\nC3. In a circle of diameter 1 consider 65 points no three of which are collinear. Prove that there exist 3 among these points which form a triangle with area less then or equal to $\\frac{1}{72}$.\n"},"solution":{"kind":"string","value":"\nSolution. Lemma: If a triangle $A B C$ lies in a rectangle $K L M N$. with sides $K L=a$ and $L M=b$, then the area of the triangle is less then or equal to $\\frac{a b}{2}$.\n\nProof of the lemma: Writhout any loss of generality assume that among the distance of $A, B, C$ from $K L$, that of $A$ is between the other two. Let $\\ell$ be the line through $A$ and parallel to $K L$. Let $D$ be the intersection of $\\ell, B C$ and $x, y$ the distances of $B, C$ from $\\ell$ respectively. Then the area of $A B C$ equals $\\frac{A D(x+y)}{2} \\leq \\frac{a b}{2}$, since $A D \\leq a$ and $x+y \\leq b$ and we are done.\n\nNow back to our problem, let us cover the circle with 24 squares of side $\\frac{1}{6}$ and 8 other irregular and equal figures as shown in Figure 9, with boundary consisting of an arc on the circle and three line segments. Call $S=A D N M$ one of these figures. One of the line segments in the boundary of $S$ is of length $A D=A B-D B=\\sqrt{A C^{2}-B C^{2}}-\\frac{2}{6}=$ $\\sqrt{\\left(\\frac{1}{2}\\right)^{2}-\\left(\\frac{1}{6}\\right)^{2}}-\\frac{1}{3}=\\frac{\\sqrt{2}-1}{3}$. The boundary segment $M N$ goes through the center $C$ of the circle, forming with the horizontal lines an angle of $45^{\\circ}$. The point in $S$ with maximum distance from the boundary segment $A B$ is the endpoint $M$ of the arc on the boundary of $S$. This distance equals $M E=M F-E F \\stackrel{C M F=\\text { isosceles }}{=} \\frac{\\sqrt{2}}{2} C M-\\frac{1}{6}=\\frac{\\sqrt{2}}{4}-\\frac{1}{6}=\\frac{3 \\sqrt{2}-2}{12}$. So $S$ can be put inside a rectangle $R$ with sides parallel to $A D, N D$ of lengths $\\frac{\\sqrt{2}-1}{3}$ and $\\frac{3 \\sqrt{2}-2}{12}$. So the triangle formed by any three points inside this figure, has an area less or\nequal to $\\frac{1}{2} \\cdot \\frac{\\sqrt{2}-1}{3} \\cdot \\frac{3 \\sqrt{2}-2}{12}=\\frac{8-5 \\sqrt{2}}{72}<\\frac{1}{72}$.\n\nAlso, the triangle formed by any three points inside any square of side $\\frac{1}{6}$, has an area less or equal to $\\frac{1}{2} \\cdot \\frac{1}{6} \\cdot \\frac{1}{6}=\\frac{1}{72}$.\n\nBy the Pigeonhole Principle, we know that among the 65 given points there exist 3 inside the same one of the 32 squares and irregular figures of the picture covering the given circle. Then according to the above, the triangle formed by these 3 points has an area not exceeding $\\frac{1}{72}$ as wanted.\n\n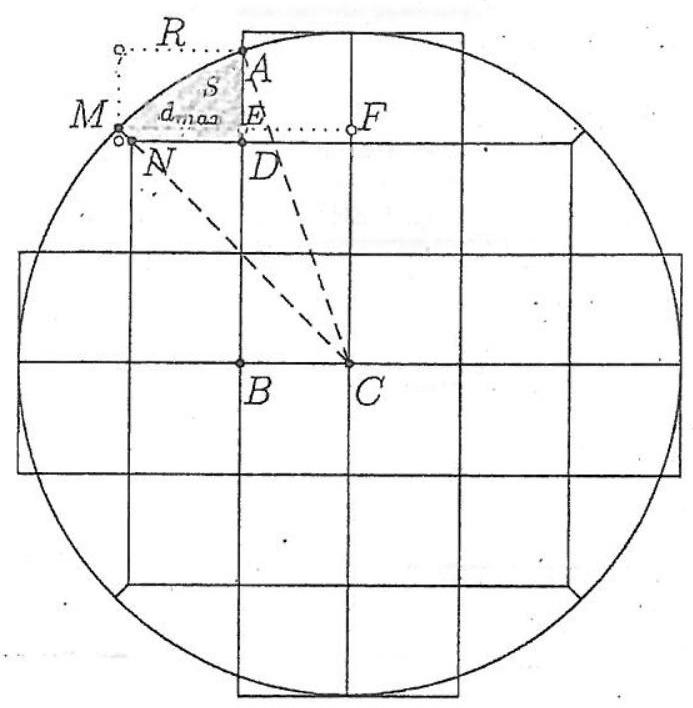![](https://cdn.mathpix.com/cropped/2024_06_05_61d3145f18c90bf9f370g-14.jpg?height=708&width=693&top_left_y=868&top_left_x=744)\n\nFigure 9: :Exercise C3.\n\n## Number Theory\n\n3 NT1. If $a, b$ are integers and $s=a^{3}+b^{3}-60 a b(a+b) \\geq 2012$, find the least possible value of $s$.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":67,"cells":{"problem":{"kind":"string","value":"\nNT5. Find all the positive integers $x, y, z, t$ such that $2^{x} \\cdot 3^{y}+5^{z}=7^{t}$.\n"},"solution":{"kind":"string","value":"\nSolution. Reducing modulo 3 we get $5^{z} \\equiv 1$, therefore $z$ is even, $z=2 c, c \\in \\mathbb{N}$. .\n\nNext we prove that $t$ is even. Obviously, $t \\geq 2$. Let us suppose that $t$ is odd, $t=2 d+1$, $d \\in \\mathbb{N}$. The equation becomes $2^{x} \\cdot 3^{y}+25^{c}=7 \\cdot 49^{d}$.\n\nIf $x \\geq 2$, reducing modulo 4 , we get $1 \\equiv 3$, contradiction.\n\nFor $x=1$, we have $2 \\cdot 3^{y}+25^{c}=7 \\cdot 49^{d}$; and, reducing modulo 24 , we obtain $2 \\cdot 3^{y}+1 \\equiv$ $7 \\Rightarrow 24 \\mid 2\\left(3^{y}-3\\right)$, i.e. $4 \\mid 3^{y-1}-1$, which means that $y-1$ is even. Then, $y=2 b+1$, $b \\in \\mathbb{N}$.\n\nWe obtain $6 \\cdot 9^{b}+25^{c}=7 \\cdot 49^{d}$, and, reducing modulo 5 , we get $(-1)^{b} \\equiv 2 \\cdot(-1)^{d}$, which is false, for all $b, d \\in \\mathbb{N}$. Hence $t$ is even, $t=2 d, d \\in \\mathbb{N}$. .\n\nThe equation can be written as $2^{x} \\cdot 3^{y}+25^{c}=49^{d} \\Leftrightarrow 2^{x} \\cdot 3^{y}=\\left(7^{d}-5^{c}\\right)\\left(7^{d}+5^{c}\\right) . \\quad$. As $\\operatorname{gcd}\\left(7^{d}-5^{c}, 7^{d}+5^{c}\\right)=2$ and $7^{c}+5^{c}>2$, there exist exactly three possibilities:(1)\n$\\left\\{\\begin{array}{l}7^{d}-5^{c}=2^{x-1} \\\\ 7^{d}+5^{c}=2 \\cdot 3^{y}\\end{array}\\right.$\n(2) $\\left\\{\\begin{array}{l}7^{d}-5^{c}=2 \\cdot 3^{y} \\\\ 7^{d}+5^{c}=2^{x-1}\\end{array}\\right.$\n(3) $\\left\\{\\begin{array}{l}7^{d}-5^{c}=2 \\\\ 7^{d}+5^{c}=2^{x-1} \\cdot 3^{y}\\end{array}\\right.$\n\nCase (1). We have $7^{d}=2^{x-2}+3^{y}$ and, reducing modulo 3 , we get $2^{x-2} \\equiv 1(\\bmod 3)$, hence $x-2$ is even, i.e. $x=2 a+2$, where $a \\in \\mathbb{N}$, since $a=0$ would mean $3^{y}+1=7^{d}$, which is impossible (even $=$ odd).\n\nWe obtain $7^{d}-5^{c}=2 \\cdot 4^{a} \\stackrel{\\text { mod } 4}{\\Longrightarrow} 7^{d} \\equiv 1(\\bmod 4) \\Rightarrow d=2 e, e \\in \\mathbb{N}$. Then $49^{e}-5^{c}=$ $2 \\cdot 4^{k} \\stackrel{\\bmod 8}{\\Longrightarrow} 5^{c} \\equiv 1(\\bmod 8) \\Rightarrow c=2 f, f \\in \\mathbb{N}$. We obtain $49^{e}-25^{f}=2: 4^{a} \\xlongequal{\\bmod 3} 0 \\equiv 2(\\bmod 3)$, false. In conclusion, in this case there are no solutions to the equation.\n\nCase (2). From $2^{x-1}=7^{d}+5^{c} \\geq 12$, we obtain $x \\geq 5$. Then $7^{d}+5^{c} \\equiv 0(\\bmod .4)$, i.e. $3^{d}+1 \\equiv 0(\\bmod 4)$, hence $d$ is odd. As $7^{d}=5^{c}+2 \\cdot 3^{y} \\geq 11$, we get $d \\geq 2$, hence $d=2 e+1$, $e \\in \\mathbb{N}$.\n\nAs in the previous case, from $7^{d}=2^{x-2}+3^{y}$, reducing modulo 3, we obtain $x=2 a+2$, with $a \\geq 2$ (because $x \\geq 5$ ). We get $7^{d}=4^{a}+3^{y}$, i.e. $7 \\cdot 49^{e}=4^{a}+3^{y}$, hence, reducing modulo 8 , we obtain $7 \\equiv 3^{y}$, which is false, because $3^{y}$ is congruent mod8 either to 1 (if $y$ is even) or to. 3 (if $y$ is odd). In conclusion, in this case there are no solutions to the equation. $k \\in \\mathbb{N}$.\n\nCase (3). From $7^{d}=5^{c}+2$, it follows that the last digit of $7^{d}$ is 7 , hence $d=4 k+1$, false.\n\nIf $c \\geq 2$, from $7^{4 k+1}=5^{c}+2$, reducing modulo 25 , we obtain $7 \\equiv 2(\\bmod 25)$, which is\n\nFor $c=1$ we get $d=1$, and the solution $x=3, y=1, z=t=2$.\n\n3 NT6. If $a, b, c, d$ are integers and $A=2(a-2 b+c)^{4}+2(b-2 c+a)^{4}+2(c-2 a+b)^{4}$, $B=d(d+1)(d+2)(d+3)+1$, prove that $(\\sqrt{A}+1)^{2}+B$ cannot be a perfect square.\n"},"answer":{"kind":"string","value":"3,1,=2"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":68,"cells":{"problem":{"kind":"string","value":"\nA1. Find all ordered triples $(x, y, z)$ of real numbers satisfying the following system of equations:\n\n$$\n\\begin{aligned}\nx^{3} & =\\frac{z}{y}-2 \\frac{y}{z} \\\\\ny^{3} & =\\frac{x}{z}-2 \\frac{z}{x} \\\\\nz^{3} & =\\frac{y}{x}-2 \\frac{x}{y}\n\\end{aligned}\n$$\n"},"solution":{"kind":"string","value":"\nSolution. We have\n\n$$\n\\begin{aligned}\n& x^{3} y z=z^{2}-2 y^{2} \\\\\n& y^{3} z x=x^{2}-2 z^{2} \\\\\n& z^{3} x y=y^{2}-2 x^{2}\n\\end{aligned}\n$$\n\nwith $x y z \\neq 0$.\n\nAdding these up we obtain $\\left(x^{2}+y^{2}+z^{2}\\right)(x y z+1)=0$. Hence $x y z=-1$. Now the system of equations becomes:\n\n$$\n\\begin{aligned}\n& x^{2}=2 y^{2}-z^{2} \\\\\n& y^{2}=2 z^{2}-x^{2} \\\\\n& z^{2}=2 x^{2}-y^{2}\n\\end{aligned}\n$$\n\nThen the first two equations give $x^{2}=y^{2}=z^{2}$. As $x y z=-1$, we conclude that $(x, y, z)=$ $(1,1,-1),(1,-1,1),(-1,1,1)$ and $(-1,-1,-1)$ are the only solutions.\n"},"answer":{"kind":"string","value":"(1,1,-1),(1,-1,1),(-1,1,1),(-1,-1,-1)"},"problem_type":{"kind":"string","value":"Algebra"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":69,"cells":{"problem":{"kind":"string","value":"\nA2. Find the largest possible value of the expression $\\left|\\sqrt{x^{2}+4 x+8}-\\sqrt{x^{2}+8 x+17}\\right|$ where $x$ is a real number.\n"},"solution":{"kind":"string","value":"\nSolution. We observe that\n\n$$\n\\left|\\sqrt{x^{2}+4 x+8}-\\sqrt{x^{2}+8 x+17}\\right|=\\left|\\sqrt{(x-(-2))^{2}+(0-2)^{2}}-\\sqrt{\\left.(x-(-4))^{2}+(0-1)^{2}\\right)}\\right|\n$$\n\nis the absolute difference of the distances from the point $P(x, 0)$ in the $x y$-plane to the points $A(-2,2)$ and $B(-4,1)$.\n\nBy the Triangle Inequality, $|P A-P B| \\leq|A B|$ and the equality occurs exactly when $P$ lies on the line passing through $A$ and $B$, but not between them.\n\nIf $P, A, B$ are collinear, then $(x-(-2)) /(0-2)=((-4)-(-2)) /(1-2)$. This gives $x=-6$, and as $-6<-4<-2$,\n\n$$\n\\left|\\sqrt{(-6)^{2}+4(-6)+8}-\\sqrt{(-6)^{2}+8(-6)+17}\\right|=|\\sqrt{20}-\\sqrt{5}|=\\sqrt{5}\n$$\n\nis the largest possible value of the expression.\n"},"answer":{"kind":"string","value":"\\sqrt{5}"},"problem_type":{"kind":"string","value":"Algebra"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":70,"cells":{"problem":{"kind":"string","value":"\nA3. Show that\n\n$$\n\\left(a+2 b+\\frac{2}{a+1}\\right)\\left(b+2 a+\\frac{2}{b+1}\\right) \\geq 16\n$$\n\nfor all positive real numbers $a, b$ satisfying $a b \\geq 1$.\n"},"solution":{"kind":"string","value":"\nSolution 1. By the AM-GM Inequality we have:\n\n$$\n\\frac{a+1}{2}+\\frac{2}{a+1} \\geq 2\n$$\n\nTherefore\n\n$$\na+2 b+\\frac{2}{a+1} \\geq \\frac{a+3}{2}+2 b\n$$\n\nand, similarly,\n\n$$\nb+2 a+\\frac{2}{b+1} \\geq 2 a+\\frac{b+3}{2}\n$$\n\nOn the other hand,\n\n$$\n(a+4 b+3)(b+4 a+3) \\geq(\\sqrt{a b}+4 \\sqrt{a b}+3)^{2} \\geq 64\n$$\n\nby the Cauchy-Schwarz Inequality as $a b \\geq 1$, and we are done.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":71,"cells":{"problem":{"kind":"string","value":"\nC3. All possible pairs of $n$ apples are weighed and the results are given to us in an arbitrary order. Can we determine the weights of the apples if a. $n=4$, b. $n=5$, c. $n=6$ ?\n"},"solution":{"kind":"string","value":"\nSolution. a. No. Four apples with weights $1,5,7,9$ and with weights $2,4,6,10$ both give the results $6,8,10,12,14,16$ when weighed in pairs.\n\nb. Yes. Let $a \\leq b \\leq c \\leq d \\leq e$ be the weights of the apples. As each apple is weighed 4 times, by adding all 10 pairwise weights and dividing the sum by 4 , we obtain $a+b+c+d+e$. Subtracting the smallest and the largest pairwise weights $a+b$ and $d+e$ from this we obtain c. Subtracting $c$ from the second largest pairwise weight $c+e$ we obtain $e$. Subtracting $e$ from the largest pairwise weight $d+e$ we obtain $d$. $a$ and $b$ are similarly determined.\n\nc. Yes. Let $a \\leq b \\leq c \\leq d \\leq e \\leq f$ be the weights of the apples. As each apple is weighed 5 times, by adding all 15 pairwise weights and dividing the sum by 5 , we obtain $a+b+c+d+e+f$. Subtracting the smallest and the largest pairwise weights $a+b$ and $e+f$ from this we obtain $c+d$.\n\nSubtracting the smallest and the second largest pairwise weights $a+b$ and $d+f$ from $a+b+c+d+e+f$ we obtain $c+e$. Similarly we obtain $b+d$. We use these to obtain $a+f$ and $b+e$.\n\nNow $a+d, a+e, b+c$ are the three smallest among the remaining six pairwise weights. If we add these up, subtract the known weights $c+d$ and $b+e$ form the sum and divide the difference by 2 , we obtain $a$. Then the rest follows.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Combinatorics"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":72,"cells":{"problem":{"kind":"string","value":"\nG1. Let $A B$ be a diameter of a circle $\\omega$ with center $O$ and $O C$ be a radius of $\\omega$ which is perpendicular to $A B$. Let $M$ be a point on the line segment $O C$. Let $N$ be the second point of intersection of the line $A M$ with $\\omega$, and let $P$ be the point of intersection of the lines tangent to $\\omega$ at $N$ and at $B$. Show that the points $M, O, P, N$ are concyclic.\n"},"solution":{"kind":"string","value":"\nSolution. Since the lines $P N$ and $B P$ are tangent to $\\omega, N P=P B$ and $O P$ is the bisector of $\\angle N O B$. Therefore the lines $O P$ and $N B$ are perpendicular. Since $\\angle A N B=90^{\\circ}$, it follows that the lines $A N$ and $O P$ are parallel. As $M O$ and $P B$ are also parallel and $A O=O B$, the triangles $A M O$ and $O P B$ are congruent and $M O=P B$. Hence $M O=N P$. Therefore $M O P N$ is an isosceles trapezoid and therefore cyclic. Hence the points $M, O, P, N$ are concyclic.\n\n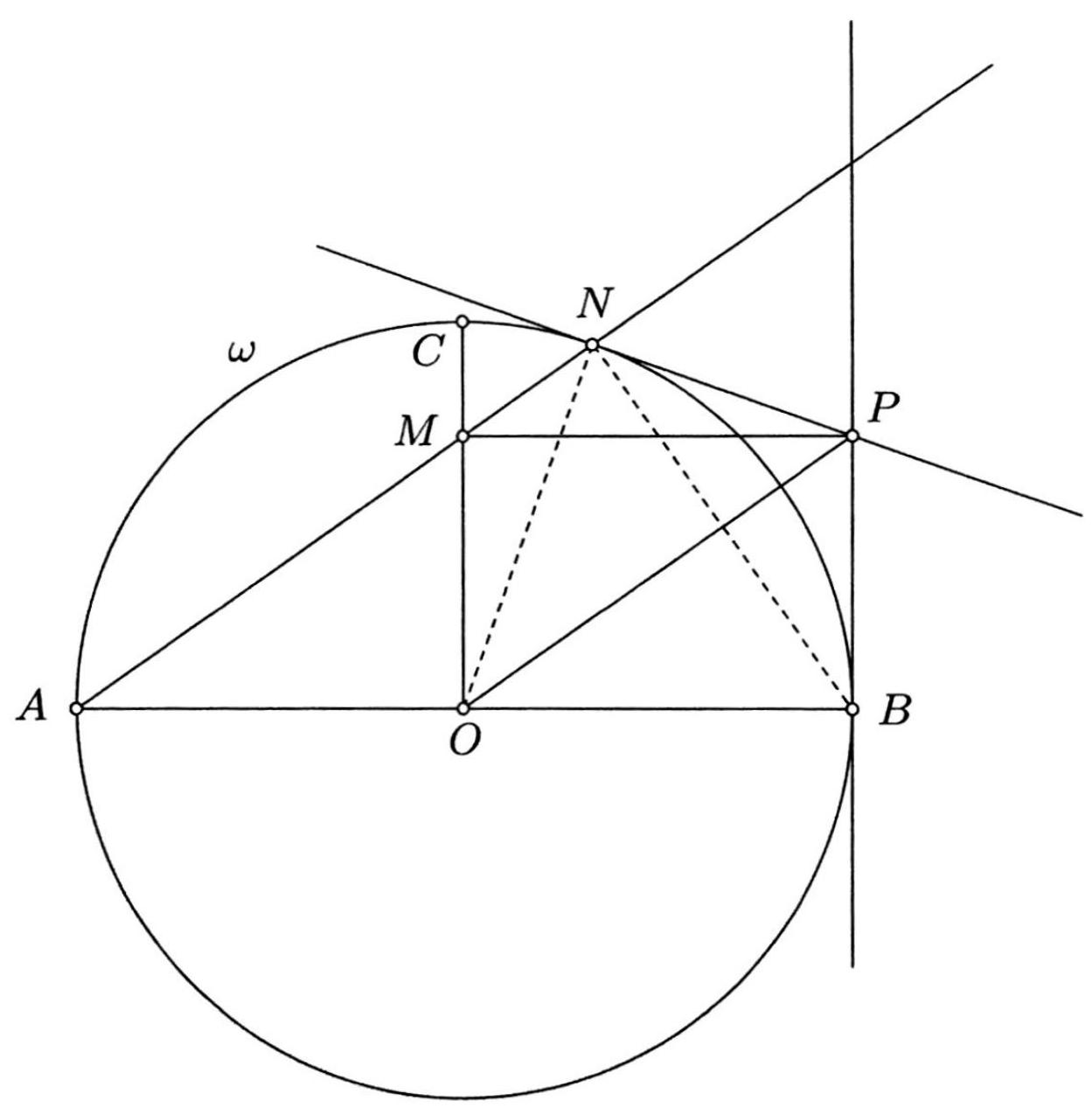![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-16.jpg?height=1267&width=1249&top_left_y=779&top_left_x=382)\n\n8.2. $\\omega_{1}$ and $\\omega_{2}$ are two circles that are externally tangent to each other at the point $M$ and internally tangent to a circle $\\omega_{3}$ at the points $K$ and $L$, respectively. Let $A$ and $B$ be the two points where the common tangent line at $M$ to $\\omega_{1}$ and $\\omega_{2}$ intersects $\\omega_{3}$. Show that if $\\angle K A B=\\angle L A B$ then the line segment $A B$ is a diameter of $\\omega_{3}$.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":73,"cells":{"problem":{"kind":"string","value":"\nG3. Let $D$ be a point on the side $B C$ of an acute triangle $A B C$ such that $\\angle B A D=\\angle C A O$ where $O$ is the center of the circumcircle $\\omega$ of the triangle $A B C$. Let $E$ be the second point of intersection of $\\omega$ and the line $A D$. Let $M, N, P$ be the midpoints of the line segments $B E, O D, A C$, respectively. Show that $M, N, P$ are collinear.\n"},"solution":{"kind":"string","value":"\nSolution. We will show that $M O P D$ is a parallelogram. From this it follows that $M, N$, $P$ are collinear.\n\nSince $\\angle B A D=\\angle C A O=90^{\\circ}-\\angle A B C, D$ is the foot of the perpendicular from $A$ to side $B C$. Since $M$ is the midpoint of the line segment $B E$, we have $B M=M E=M D$ and hence $\\angle M D E=\\angle M E D=\\angle A C B$.\n\nLet the line $M D$ intersect the line $A C$ at $D_{1}$. Since $\\angle A D D_{1}=\\angle M D E=\\angle A C D, M D$ is perpendicular to $A C$. On the other hand, since $O$ is the center of the circumcircle of triangle $A B C$ and $P$ is the midpoint of the side $A C, O P$ is perpendicular to $A C$. Therefore $M D$ and $O P$ are parallel.\n\nSimilarly, since $P$ is the midpoint of the side $A C$, we have $A P=P C=D P$ and hence $\\angle P D C=\\angle A C B$. Let the line $P D$ intersect the line $B E$ at $D_{2}$. Since $\\angle B D D_{2}=\\angle P D C=$ $\\angle A C B=\\angle B E D$, we conclude that $P D$ is perpendicular to $B E$. Since $M$ is the midpoint of the line segment $B E, O M$ is perpendicular to $B E$ and hence $O M$ and $P D$ are parallel.\n\n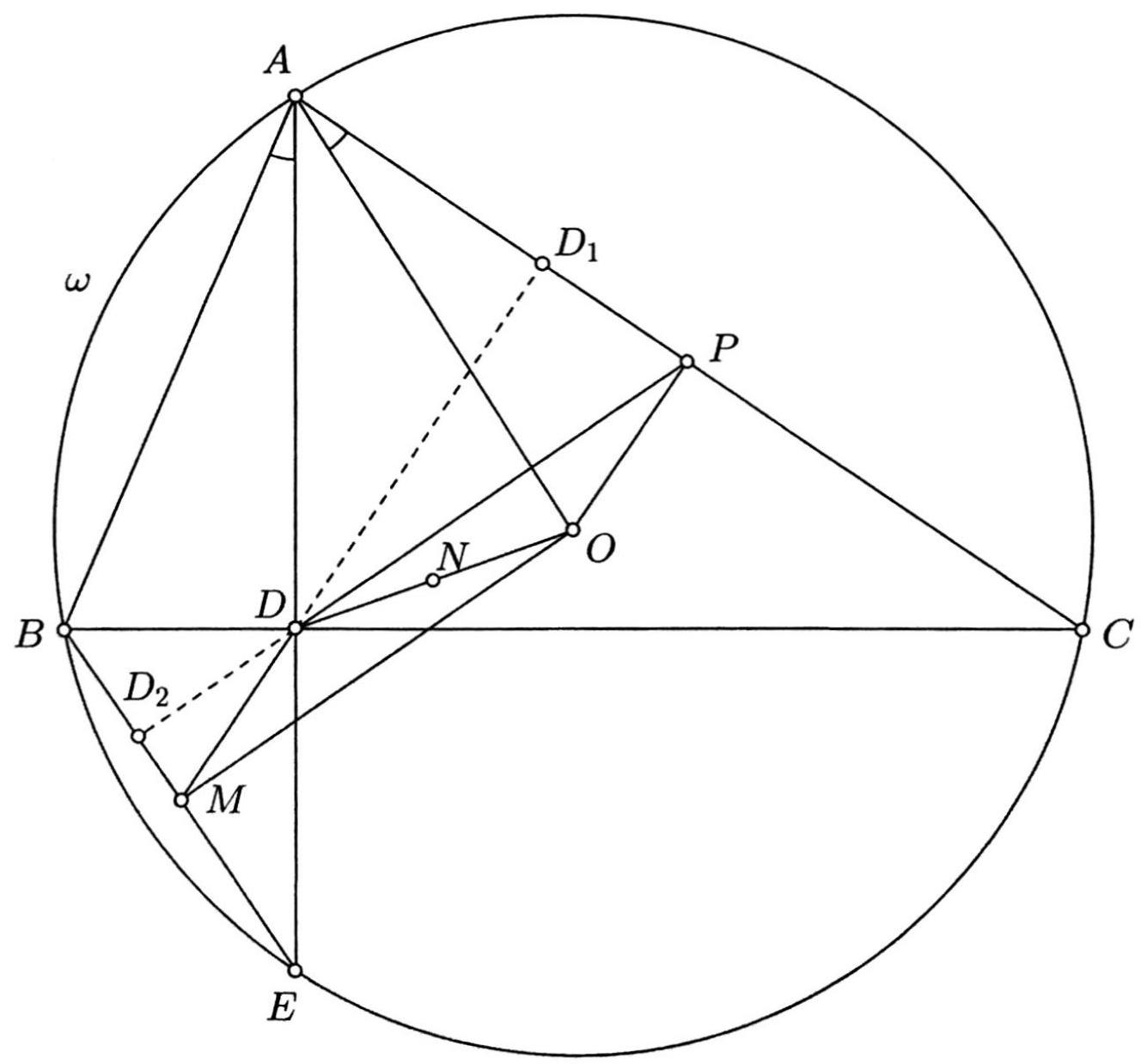![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-18.jpg?height=1238&width=1335&top_left_y=1217&top_left_x=359)\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":74,"cells":{"problem":{"kind":"string","value":"\nG4. Let $I$ be the incenter and $A B$ the shortest side of a triangle $A B C$. The circle with center $I$ and passing through $C$ intersects the ray $A B$ at the point $P$ and the ray $B A$ at the point $Q$. Let $D$ be the point where the excircle of the triangle $A B C$ belonging to angle $A$ touches the side $B C$, and let $E$ be the symmetric of the point $C$ with respect to $D$. Show that the lines $P E$ and $C Q$ are perpendicular.\n"},"solution":{"kind":"string","value":"\nSolution. First we will show that points $P$ and $Q$ are not on the line segment $A B$.\n\nAssume that $Q$ is on the line segment $A B$. Since $C I=Q I$ and $\\angle I B Q=\\angle I B C$, either the triangles $C B I$ and $Q B I$ are congruent or $\\angle I C B+\\angle I Q B=180^{\\circ}$. In the first case, we have $B C=B Q$ which contradicts $A B$ being the shortest side.\n\nIn the second case, we have $\\angle I Q A=\\angle I C B=\\angle I C A$ and the triangles $I A C$ and $I A Q$ are congruent. Hence this time we have $A C=A Q$, contradicting $A B$ being the shortest side.\n\n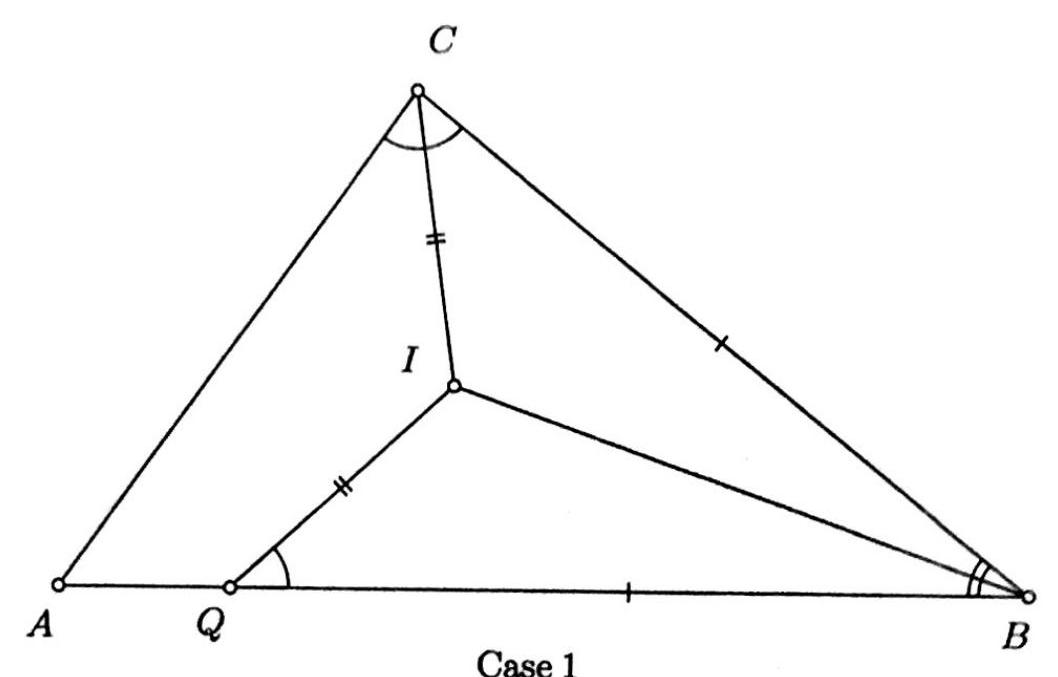![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-19.jpg?height=677&width=1058&top_left_y=874&top_left_x=520)\n\nCase 1\n\n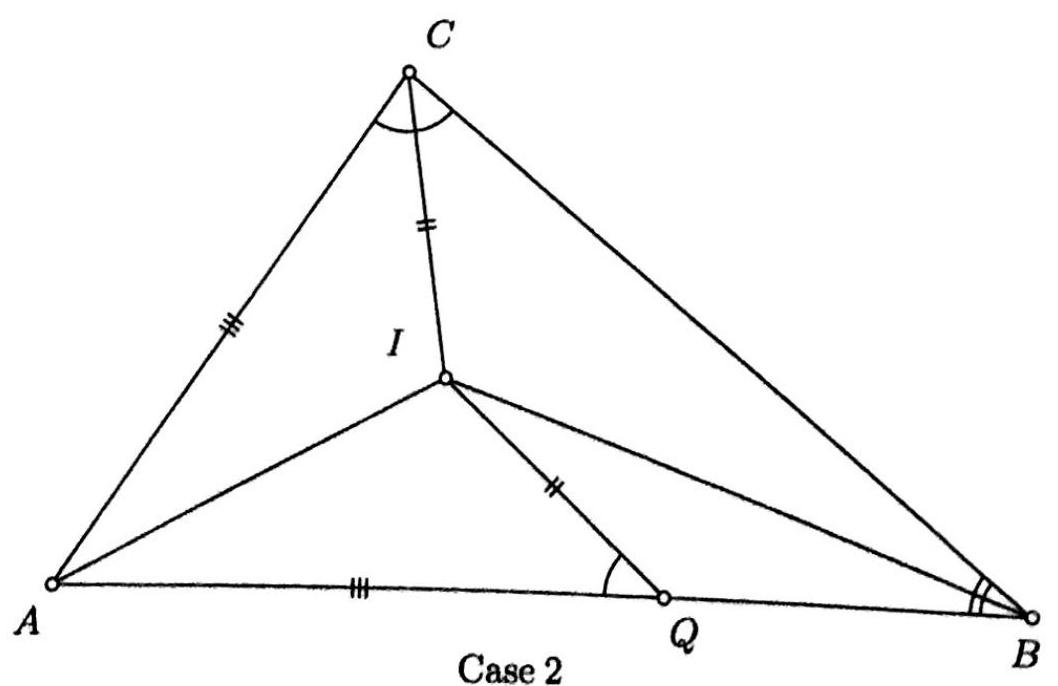![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-19.jpg?height=686&width=1058&top_left_y=1733&top_left_x=498)\n\nNow we will show that the lines $P E$ and $C Q$ are perpendicular.\n\nSince $\\angle I Q B \\leq \\angle I A B=(\\angle C A B) / 2<90^{\\circ}$ and $\\angle I C B=(\\angle A C B) / 2<90^{\\circ}$, the triangles $C B I$ and $Q B I$ are congruent. Hence $B C=B Q$ and $\\angle C Q P=\\angle C Q B=90^{\\circ}-(\\angle A B C) / 2$. Similarly, we have $A C=A P$ and hence $B P=A C-A B$.\n\nOn the other hand, as $D E=C D$ and $C D+A C=u$, where $u$ denotes the semiperimeter of the triangle $A B C$, we have $B E=B C-2(u-A C)=A C-A B$. Therefore $B P=B E$ and $\\angle Q P E=(\\angle A B C) / 2$.\n\nHence, $\\angle C Q P+\\angle Q P E=90^{\\circ}$.\n\n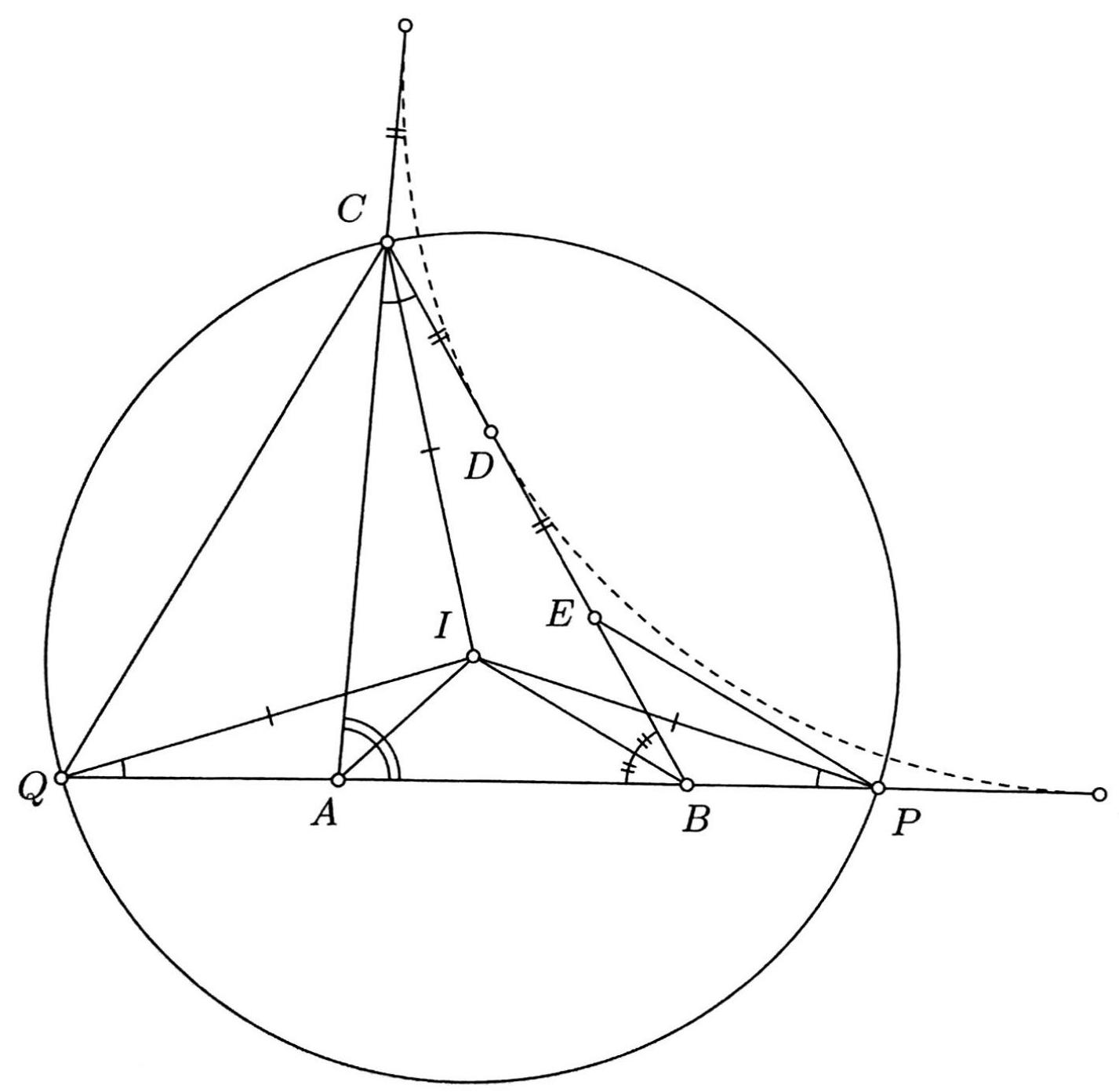![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-20.jpg?height=1393&width=1427&top_left_y=773&top_left_x=333)\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":75,"cells":{"problem":{"kind":"string","value":"\nG5. A circle passing through the midpoint $M$ of the side $B C$ and the vertex $A$ of a triangle $A B C$ intersects the sides $A B$ and $A C$ for the second time at the points $P$ and $Q$, respectively. Show that if $\\angle B A C=60^{\\circ}$ then\n\n$$\nA P+A Q+P Q<A B+A C+\\frac{1}{2} B C\n$$\n"},"solution":{"kind":"string","value":"\nSolution. Since the quadrilateral $A P M Q$ is cyclic, we have $\\angle P M Q=180^{\\circ}-\\angle P A Q=$ $180^{\\circ}-\\angle B A C=120^{\\circ}$. Therefore $\\angle P M B+\\angle Q M C=180^{\\circ}-\\angle P M Q=60^{\\circ}$.\n\nLet the point $B^{\\prime}$ be the symmetric of the point $B$ with respect to the line $P M$ and the point $C^{\\prime}$ be the symmetric of the point $C$ with respect to the line $Q M$. The triangles $B^{\\prime} M P$ and $B M P$ are congruent and the triangles $C^{\\prime} M Q$ and $C M Q$ are congruent. Hence $\\angle B^{\\prime} M C^{\\prime}=\\angle P M Q-\\angle B^{\\prime} M P-\\angle C^{\\prime} M Q=120^{\\circ}-\\angle B M P-\\angle C M Q=120^{\\circ}-60^{\\circ}=60^{\\circ}$. As we also have $B^{\\prime} M=B M=C M=C^{\\prime} M$, we conclude that the triangle $B^{\\prime} M C^{\\prime}$ is equilateral and $B^{\\prime} C^{\\prime}=B C / 2$.\n\n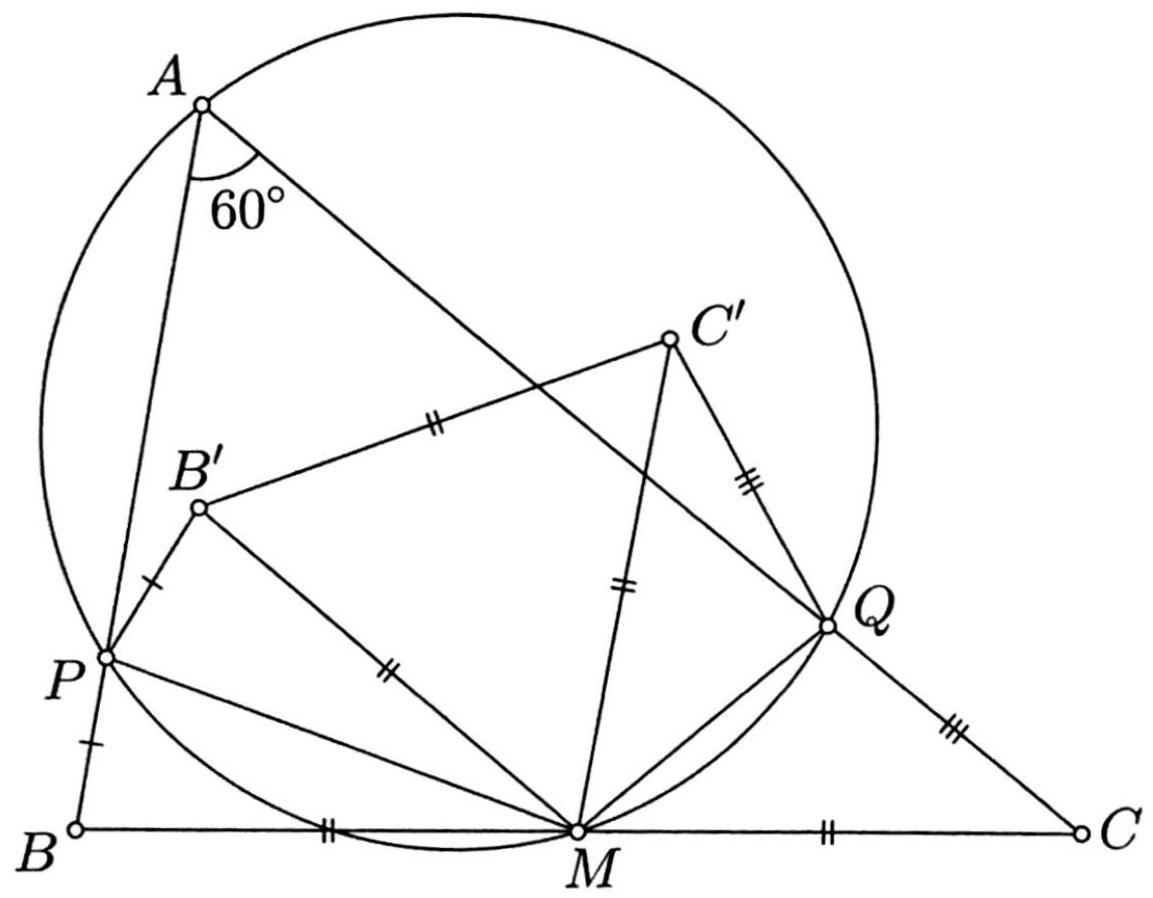![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-21.jpg?height=898&width=1153&top_left_y=978&top_left_x=493)\n\nOn the other hand, we have $P B^{\\prime}+B^{\\prime} C^{\\prime}+C^{\\prime} Q \\geq P Q$ by the Triangle Inequality, and hence $P B+B C / 2+Q C \\geq P Q$. This gives the inequality $A B+B C / 2+A C \\geq A P+P Q+A Q$.\n\nWe get an equality only when the points $B^{\\prime}$ and $C^{\\prime}$ lie on the line segment $P Q$. If this is the case, then $\\angle P Q C+\\angle Q P B=2(\\angle P Q M+\\angle Q P M)=120^{\\circ}$ and therefore $\\angle A P Q+\\angle A Q P=$ $240^{\\circ} \\neq 120^{\\circ}$, a contradiction.\n$A B C D$. Let $K$ and $M$ be the points of intersection of the line $P D$ with $Q B$ and $Q A$, respectively, and let $N$ be the point of intersection of the lines $P A$ and $Q B$.\n\nLet $X, Y, Z$ be the midpoints of the line segments $A N, K N, A M$, respectively. Let $\\ell_{1}$ be the line passing through $X$ and perpendicular to $M K, \\ell_{2}$ be the line passing through $Y$ and perpendicular to $A M, \\ell_{3}$ be the line passing through $Z$ and perpendicular to $K N$. Show that $\\ell_{1}, \\ell_{2}, \\ell_{3}$ are concurrent.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":76,"cells":{"problem":{"kind":"string","value":"\nN1. Find all positive integere on for othich $1^{2}+2^{2}+\\cdots+16^{2}+17$ is a perfort square\n"},"solution":{"kind":"string","value":"\nSolution. We bave $1^{3}+2^{5}+\\cdots+16^{2}=(1+2+\\cdots+16)^{2}=5^{2} \\quad 17^{0}$ Herese. $11^{3}+2^{3}+$\n\n![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-24.jpg?height=83&width=1607&top_left_y=309&top_left_x=263)\nmeeger t then $1 T^{\\prime}-(1+B)(t-3)$ A. $(1,5) \\quad(t-3)=16$ this can coly happen\n\n![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-24.jpg?height=74&width=1467&top_left_y=415&top_left_x=206)\n\nEirornd all ordered triples $(x, y, z)$ of integers satisfying $20^{x}+13^{y}=2013^{z}$.\n"},"answer":{"kind":"string","value":""},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Incomplete"},"solution_is_valid":{"kind":"string","value":"Incomplete"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":77,"cells":{"problem":{"kind":"string","value":"\nN3. Find all ordered pairs $(a, b)$ of positive integers for which the numbers $\\frac{a^{3} b-1}{a+1}$ and $\\frac{b^{3} a+1}{b-1}$ are positive integers.\n"},"solution":{"kind":"string","value":"\nSolution. As $a^{3} b-1=b\\left(a^{3}+1\\right)-(b+1)$ and $a+1 \\mid a^{3}+1$, we have $a+1 \\mid b+1$.\n\nAs $b^{3} a+1=a\\left(b^{3}-1\\right)+(a+1)$ and $b-1 \\mid b^{3}-1$, we have $b-1 \\mid a+1$.\n\nSo $b-1 \\mid b+1$ and hence $b-1 \\mid 2$.\n\n- If $b=2$, then $a+1 \\mid b+1=3$ gives $a=2$. Hence $(a, b)=(2,2)$ is the only solution in this case.\n- If $b=3$, then $a+1 \\mid b+1=4$ gives $a=1$ or $a=3$. Hence $(a, b)=(1,3)$ and $(3,3)$ are the only solutions in this case.\n\nTo summarize, $(a, b)=(1,3),(2,2)$ and $(3,3)$ are the only solutions.\n$\\mathbf{N 4}$. A rectangle in the $x y$-plane is called latticed if all its vertices have integer coordinates.\n\na. Find a latticed rectangle with area 2013 whose sides are not parallel to the axes.\n\nb. Show that if a latticed rectangle has area 2011, then its sides are parallel to the axes.\n"},"answer":{"kind":"string","value":"(1,3),(2,2),(3,3)"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":78,"cells":{"problem":{"kind":"string","value":"\nN5. Find all ordered triples $(x, y, z)$ of positive integers satisfying the equation\n\n$$\n\\frac{1}{x^{2}}+\\frac{y}{x z}+\\frac{1}{z^{2}}=\\frac{1}{2013}\n$$\n"},"solution":{"kind":"string","value":"\nSolution. We have $x^{2} z^{2}=2013\\left(x^{2}+x y z+z^{2}\\right)$. Let $d=\\operatorname{gcd}(x, z)$ and $x=d a, z=d b$. Then $a^{2} b^{2} d^{2}=2013\\left(a^{2}+a b y+b^{2}\\right)$.\n\nAs $\\operatorname{gcd}(a, b)=1$, we also have $\\operatorname{gcd}\\left(a^{2}, a^{2}+a b y+b^{2}\\right)=1$ and $\\operatorname{gcd}\\left(b^{2}, a^{2}+a b y+b^{2}\\right)=1$. Therefore $a^{2} \\mid 2013$ and $b^{2} \\mid 2013$. But $2013=3 \\cdot 11 \\cdot 61$ is squarefree and therefore $a=1=b$.\n\nNow we have $x=z=d$ and $d^{2}=2013(y+2)$. Once again as 2013 is squarefree, we must have $y+2=2013 n^{2}$ where $n$ is a positive integer.\n\nHence $(x, y, z)=\\left(2013 n, 2013 n^{2}-2,2013 n\\right)$ where $n$ is a positive integer.\n"},"answer":{"kind":"string","value":"(x,y,z)=(2013n,2013n^{2}-2,2013n)"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":79,"cells":{"problem":{"kind":"string","value":"\nN6. Find all ordered triples $(x, y, z)$ of integers satisfying the following system of equations:\n\n$$\n\\begin{aligned}\nx^{2}-y^{2} & =z \\\\\n3 x y+(x-y) z & =z^{2}\n\\end{aligned}\n$$\n"},"solution":{"kind":"string","value":"\nSolution. If $z=0$, then $x=0$ and $y=0$, and $(x, y, z)=(0,0,0)$.\n\nLet us assume that $z \\neq 0$, and $x+y=a$ and $x-y=b$ where $a$ and $b$ are nonzero integers such that $z=a b$. Then $x=(a+b) / 2$ and $y=(a-b) / 2$, and the second equations gives $3 a^{2}-3 b^{2}+4 a b^{2}=4 a^{2} b^{2}$.\n\nHence\n\n$$\nb^{2}=\\frac{3 a^{2}}{4 a^{2}-4 a+3}\n$$\n\nand\n\n$$\n3 a^{2} \\geq 4 a^{2}-4 a+3\n$$\n\nwhich is satisfied only if $a=1,2$ or 3 .\n\n- If $a=1$, then $b^{2}=1 .(x, y, z)=(1,0,1)$ and $(0,1,-1)$ are the only solutions in this case.\n- If $a=2$, then $b^{2}=12 / 11$. There are no solutions in this case\n- If $a=3$, then $b^{2}=1 .(x, y, z)=(1,2,-3)$ and $(2,1,3)$ are the only solutions in this case.\n\nTo summarize, $(x, y, z)=(0,0,0),(1,0,1),(0,1,-1),(1,2,-3)$ and $(2,1,3)$ are the only solutions.\n\nComments. 1. The original problem proposal asks for the solutions when $z=p$ is a prime number.\n\n2. The problem can be asked with a single equation in the form:\n\n$$\n3 x y+(x-y)^{2}(x+y)=\\left(x^{2}-y^{2}\\right)^{2}\n$$\n\n"},"answer":{"kind":"string","value":"(0,0,0),(1,0,1),(0,1,-1),(1,2,-3),(2,1,3)"},"problem_type":{"kind":"string","value":"Algebra"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":80,"cells":{"problem":{"kind":"string","value":"## A1 MLD\n\nLet $x, y, z$ be real numbers, satisfying the relations\n\n$$\n\\left\\{\\begin{array}{l}\nx \\geq 20 \\\\\ny \\geq 40 \\\\\nz \\geq 1675 \\\\\nx+y+z=2015\n\\end{array}\\right.\n$$\n\nFind the greatest value of the product $P=x \\cdot y \\cdot z$.\n\n"},"solution":{"kind":"string","value":"## Solution 1:\n\nBy virtue of $z \\geq 1675$ we have\n\n$$\ny+z<2015 \\Leftrightarrow y<2015-z \\leq 2015-1675<1675\n$$\n\nIt follows that $(1675-y) \\cdot(1675-z) \\leq 0 \\Leftrightarrow y \\cdot z \\leq 1675 \\cdot(y+z-1675)$.\n\nBy using the inequality $u \\cdot v \\leq\\left(\\frac{u+v}{2}\\right)^{2}$ for all real numbers $u, v$ we obtain\n\n$$\n\\begin{gathered}\nP=x \\cdot y \\cdot z \\leq 1675 \\cdot x \\cdot(y+z-1675) \\leq 1675 \\cdot\\left(\\frac{x+y+z-1675}{2}\\right)^{2}= \\\\\n1675 \\cdot\\left(\\frac{2015-1675}{2}\\right)^{2}=1675 \\cdot 170^{2}=48407500\n\\end{gathered}\n$$\n\n$$\n\\text { We have } P=x \\cdot y \\cdot z=48407500 \\Leftrightarrow\\left\\{\\begin{array} { l } \n{ x + y + z = 2 0 1 5 , } \\\\\n{ z = 1 6 7 5 , } \\\\\n{ x = y + z - 1 6 7 5 }\n\\end{array} \\Leftrightarrow \\left\\{\\begin{array}{l}\nx=170 \\\\\ny=170 \\\\\nz=1675\n\\end{array}\\right.\\right.\n$$\n\nSo, the greatest value of the product is $P=x \\cdot y \\cdot z=48407500$.\n\n"},"answer":{"kind":"string","value":"48407500"},"problem_type":{"kind":"string","value":"Algebra"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":81,"cells":{"problem":{"kind":"string","value":"## A2 ALB\n\n3) If $x^{3}-3 \\sqrt{3} x^{2}+9 x-3 \\sqrt{3}-64=0$, find the value of $x^{6}-8 x^{5}+13 x^{4}-5 x^{3}+49 x^{2}-137 x+2015$.\n"},"solution":{"kind":"string","value":"\nSolution\n\n$x^{3}-3 \\sqrt{3} x^{2}+9 x-3 \\sqrt{3}-64=0 \\Leftrightarrow(x-\\sqrt{3})^{3}=64 \\Leftrightarrow(x-\\sqrt{3})=4 \\Leftrightarrow x-4=\\sqrt{3} \\Leftrightarrow x^{2}-8 x+16=3 \\Leftrightarrow$ $x^{2}-8 x+13=0$\n\n$x^{6}-8 x^{5}+13 x^{4}-5 x^{3}+49 x^{2}-137 x+2015=\\left(x^{2}-8 x+13\\right)\\left(x^{4}-5 x+9\\right)+1898=0+1898=1898$\n\n"},"answer":{"kind":"string","value":"1898"},"problem_type":{"kind":"string","value":"Algebra"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":82,"cells":{"problem":{"kind":"string","value":"## A3 MNE\n\nLet $a, b, c$ be positive real numbers. Prove that\n\n$$\n\\frac{a}{b}+\\sqrt{\\frac{b}{c}}+\\sqrt[3]{\\frac{c}{a}}>2\n$$\n\n"},"solution":{"kind":"string","value":"## Solution:\n\nStarting from the double expression on the left-hand side of given inequality, and applying twice the Arithmetic-Geometric mean inequality, we find that\n\n$$\n\\begin{aligned}\n2 \\frac{a}{b}+2 \\sqrt{\\frac{b}{c}}+2 \\sqrt[3]{\\frac{c}{a}} & =\\frac{a}{b}+\\left(\\frac{a}{b}+\\sqrt{\\frac{b}{c}}+\\sqrt{\\frac{b}{c}}\\right)+2 \\sqrt[3]{\\frac{c}{a}} \\\\\n& \\geq \\frac{a}{b}+3 \\sqrt[3]{\\frac{a}{b}} \\sqrt{\\frac{b}{c}} \\sqrt{\\frac{b}{c}}+2 \\sqrt[3]{\\frac{c}{a}} \\\\\n& =\\frac{a}{b}+3 \\sqrt[3]{\\frac{a}{c}}+2 \\sqrt[3]{\\frac{c}{a}} \\\\\n& \\left.=\\frac{a}{b}+\\sqrt[3]{\\frac{a}{c}}+2 \\sqrt[3]{\\frac{a}{c}}+\\sqrt[3]{\\frac{c}{a}}\\right) \\\\\n& \\geq \\frac{a}{b}+\\sqrt[3]{\\frac{a}{c}}+2 \\cdot 2 \\sqrt{\\sqrt[3]{\\frac{a}{c}} \\sqrt[3]{\\frac{c}{a}}} \\\\\n& =\\frac{a}{b}+\\sqrt[3]{\\frac{a}{c}}+4 \\\\\n& >4\n\\end{aligned}\n$$\n\nwhich yields the given inequality.\n\n(A4) GRE\n\nLet $a, b, c$ be positive real numbers such that $a+b+c=3$. Find the minimum value of\n\n$$\nA=\\frac{2-a^{3}}{a}+\\frac{2-b^{3}}{b}+\\frac{2-c^{3}}{c}\n$$\n\n"},"answer":{"kind":"string","value":"4"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":83,"cells":{"problem":{"kind":"string","value":"## A5 MKCD\n\nLet $x, y, z$ be positive real numbers that satisfy the equality $x^{2}+y^{2}+z^{2}=3$. Prove that\n\n$$\n\\frac{x^{2}+y z}{x^{2}+y z+1}+\\frac{y^{2}+z x}{y^{2}+z x+1}+\\frac{z^{2}+x y}{z^{2}+x y+1} \\leq 2\n$$\n\n"},"solution":{"kind":"string","value":"## Solution:\n\nWe have\n\n$$\n\\begin{aligned}\n& \\frac{x^{2}+y z}{x^{2}+y z+1}+\\frac{y^{2}+z x}{y^{2}+z x+1}+\\frac{z^{2}+x y}{z^{2}+x y+1} \\leq 2 \\Leftrightarrow \\\\\n& \\frac{x^{2}+y z+1}{x^{2}+y z+1}+\\frac{y^{2}+z x+1}{y^{2}+z x+1}+\\frac{z^{2}+x y+1}{z^{2}+x y+1} \\leq 2+\\frac{1}{x^{2}+y z+1}+\\frac{1}{y^{2}+z x+1}+\\frac{1}{z^{2}+x y+1} \\Leftrightarrow \\\\\n& 3 \\leq 2+\\frac{1}{x^{2}+y z+1}+\\frac{1}{y^{2}+z x+1}+\\frac{1}{z^{2}+x y+1} \\Leftrightarrow \\\\\n& 1 \\leq \\frac{1}{x^{2}+y z+1}+\\frac{1}{y^{2}+z x+1}+\\frac{1}{z^{2}+x y+1} \\\\\n& \\frac{1}{x^{2}+y z+1}+\\frac{1}{y^{2}+z x+1}+\\frac{1}{z^{2}+x y+1} \\geq \\frac{9}{x^{2}+y z+1+y^{2}+z x+1+z^{2}+x y+1}= \\\\\n& \\frac{9}{x^{2}+y^{2}+z^{2}+x y+y z+z x+3} \\geq \\frac{9}{2 x^{2}+y^{2}+z^{2}+3}=1\n\\end{aligned}\n$$\n\nThe first inequality: AM-GM inequality (also can be achieved with Cauchy-BunjakowskiSchwarz inequality). The second inequality: $x y+y z+z x £ x^{2}+y^{2}+z^{2}$ (there are more ways to prove it, AM-GM, full squares etc.)\n\n## GEOMETRY\n\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Inequalities"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":84,"cells":{"problem":{"kind":"string","value":"## G1 MNE\n\nAround the triangle $A B C$ the circle is circumscribed, and at the vertex $C$ tangent $t$ to this circle is drawn. The line $p$ which is parallel to this tangent intersects the lines $B C$ and $A C$ at the points $D$ and $E$, respectively. Prove that the points $A, B, D, E$ belong to the same circle.\n\n"},"solution":{"kind":"string","value":"## Solution:\n\nLet $O$ be the center of a circumscribed circle $k$ of the triangle $A B C$, and let $F$ and $G$ be the points of intersection of the line $C O$ with the line $p$ and the circle $k$, respectively (see Figure). From $p \\| t$ it follows that $p \\perp C O$. Furthermore, $\\angle A B C=\\angle A G C$, because these angles are peripheral over the same chord. The quadrilateral $A G F E$ has two right angles at the vertices $A$ and $F$, and hence, $\\angle A E D+\\angle A B D=\\angle A E F+\\angle A G F=180^{\\circ}$. Hence, the quadrilateral $A B D E$ is cyclic, as asserted.\n\n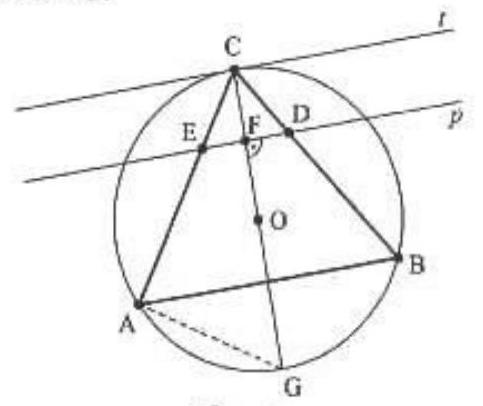![](https://cdn.mathpix.com/cropped/2024_06_05_07a1b610f48bd7c35addg-06.jpg?height=406&width=483&top_left_y=2006&top_left_x=843)\n\nFigure\n\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":85,"cells":{"problem":{"kind":"string","value":"## G2 MLD\n\nThe point $P$ is outside of the circle $\\Omega$. Two tangent lines, passing from the point $P$, touch the circle $\\Omega$ at the points $A$ and $B$. The median $A M, M \\in(B P)$, intersects the circle $\\Omega$ at the point $C$ and the line $P C$ intersects again the circle $\\Omega$ at the point $D$. Prove that the lines $A D$ and $B P$ are parallel.\n\n"},"solution":{"kind":"string","value":"## Solution:\n\nSince $\\angle B A C=\\angle B A M=\\angle M B C$, we have $\\triangle M A B \\cong \\triangle M B C$.\n\n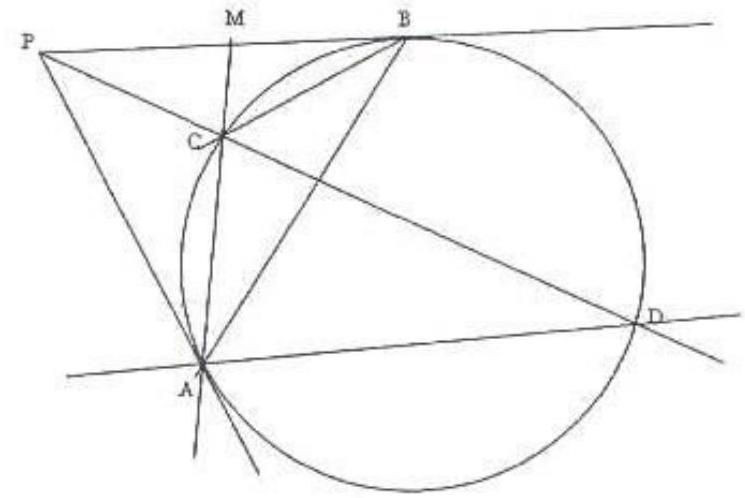![](https://cdn.mathpix.com/cropped/2024_06_05_07a1b610f48bd7c35addg-07.jpg?height=498&width=745&top_left_y=735&top_left_x=625)\n\nWe obtain $\\frac{M A}{M B}=\\frac{M B}{M C}=\\frac{A B}{B C}$. The equality $\\quad M B=M P$ implies $\\frac{M A}{M P}=\\frac{M P}{M C}$ and $\\angle P M C \\equiv \\angle P M A$ gives the relation $\\triangle P M A \\cong \\triangle C M P$. It follows that $\\angle B P D \\equiv \\angle M P C \\equiv \\angle M A P \\equiv \\angle C A P \\equiv \\angle C D A \\equiv \\angle P D A$. So, the lines $A D$ and $B P$ are parallel.\n\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":86,"cells":{"problem":{"kind":"string","value":"## G3 GRE\n\nLet $c \\equiv c(O, K)$ be a circle with center $O$ and radius $R$ and $A, B$ be two points on it, not belonging to the same diameter. The bisector of the angle $A \\hat{B} O$ intersects the circle $c$ at point $C$, the circumcircle of the triangle $A O B$, say ${ }^{c_{1}}$ at point $K$ and the circumcircle of the triangle $A O C$, say ${ }^{c_{2}}$, at point $L$. Prove that the point $K$ is the circumcenter of the triangle $A O C$ and the point $L$ is the incenter of the triangle $A O B$.\n\n"},"solution":{"kind":"string","value":"## Solution:\n\nThe segments $O B, O C$ are equal, as radii of the circle ${ }^{c}$. Hence $O B C$ is an isosceles triangle and\n\n$$\n\\hat{B}_{1}=\\hat{C}_{1}=\\hat{x}\n$$\n\n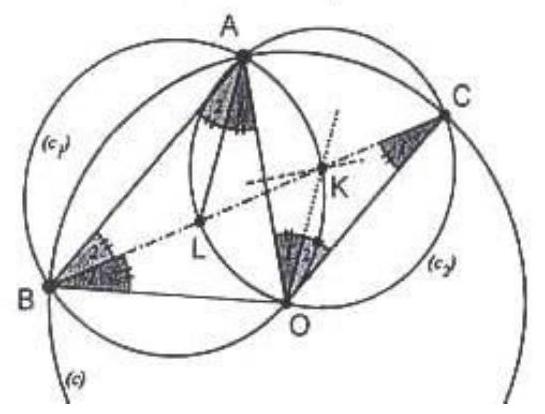![](https://cdn.mathpix.com/cropped/2024_06_05_07a1b610f48bd7c35addg-07.jpg?height=414&width=545&top_left_y=2097&top_left_x=714)\n\nThe chord $B C$ is the bisector of the angle $O \\hat{B} A$, and hence\n\n$$\n\\hat{B}_{1}=\\hat{B}_{2}=\\hat{x}\n$$\n\nThe angles $\\hat{B}_{2}$ and $\\hat{O}_{1}$ are inscribed to the same arc $O K$ of the circle ${ }^{c_{1}}$ and hence\n\n$$\n\\hat{B}_{2}=\\hat{\\mathrm{O}}_{1}=\\hat{x}\n$$\n\nThe segments $K O, K C$ are equal, as radii of the circle ${ }^{c_{2}}$. Hence the triangle $K O C$ is isosceles and so\n\n$$\n\\hat{O}_{2}=\\hat{C}_{1}=\\hat{x}\n$$\n\nFrom equalities $(1),(2),(3)$ we conclude that\n\n$$\n\\hat{O}_{1}=\\hat{O}_{2}=\\hat{x}\n$$\n\nand so $O K$ is the bisector, and hence perpendicular bisector of the isosceles triangle $O A C$. The point $K$ is the middle of the arc $O K$ (since $B K$ bisects the angle $O \\hat{B} A$ ). Hence the perpendicular bisector of the chord $A O$ of the circle ${ }^{c_{1}}$ is passing through point $K$. It means that $K$ is the circumcenter of the triangle $O A C$.\n\nFrom equalities (1),(2),(3) we conclude that $\\hat{B}_{2}=\\hat{C}_{1}=\\hat{x}$ and so $A B / / O C \\Rightarrow O \\hat{A} B=A \\hat{O} C$, that is $\\hat{A}_{1}+\\hat{A}_{2}=\\hat{O}_{1}+\\hat{O}_{2}$ and since $\\hat{O}_{1}=\\hat{O}_{2}=\\hat{x}$, we conclude that\n\n$$\n\\hat{A}_{1}+\\hat{A}_{2}=2 \\hat{O}_{1}=2 \\hat{x}\n$$\n\nThe angles $\\hat{A}_{I}$ and $\\hat{C}_{I}$ are inscribed into the circle ${ }^{c_{2}}$ and correspond to the same arc $O L$. Hence\n\n$$\n\\hat{A}_{I}=\\hat{C}_{1}=\\hat{x}\n$$\n\nFrom (5) and (6) we have $\\hat{A}_{1}=\\hat{A}_{2}$, i.e. $A L$ is the bisector of the angle $B \\hat{A} O$.\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":87,"cells":{"problem":{"kind":"string","value":"\nG4\n\nCYP\n\nLet $\\triangle A B C$ be an acute triangle. The lines $\\left(\\varepsilon_{1}\\right),\\left(\\varepsilon_{2}\\right)$ are perpendicular to $A B$ at the points $A$, $B$, respectively. The perpendicular lines from the midpoint $M$ of $A B$ to the sides of the triangle $A C_{;} B C$ intersect the lines $\\left(\\varepsilon_{1}\\right),\\left(\\xi_{2}\\right)$ at the points $E, F$, respectively. If $I$ is the intersection point of $E F, M C$, prove that\n\n$$\n\\angle A I B=\\angle E M F=\\angle C A B+\\angle C B A\n$$\n\n"},"solution":{"kind":"string","value":"## Solution:\n\nLet $H, G$ be the points of intersection of $M E, M F$, with $A C, B C$ respectively. From the similarity of triangles $\\triangle M H A$ and $\\triangle M A E$ we get\n\n$$\n\\frac{M H}{M A}=\\frac{M A}{M E}\n$$\n\nthus, $M A^{2}=M H \\cdot M E$\n\nSimilarly, from the similarity of triangles $\\triangle M B G$ and $\\triangle M F B$ we get\n\n$$\n\\frac{M B}{M F}=\\frac{M G}{M B}\n$$\n\nthus, $M B^{2}=M F \\cdot M G$\n\nSince $M A=M B$, from (1), (2), we have that the points $E, H, G, F$ are concyclic.\n\n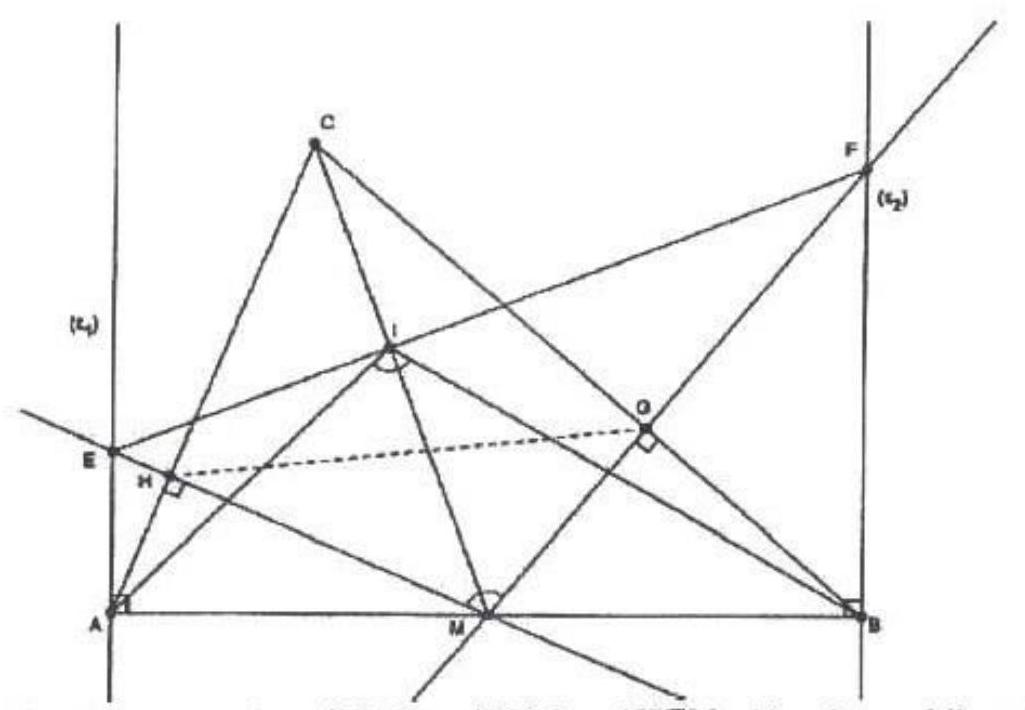![](https://cdn.mathpix.com/cropped/2024_06_05_07a1b610f48bd7c35addg-09.jpg?height=710&width=1025&top_left_y=298&top_left_x=298)\n\nTherefore, we get that $\\angle F E H=\\angle F E M=\\angle H G M$. Also, the quadrilateral $C H M G$ is cyclic, so $\\angle C M H=\\angle H G C$. We have\n\n$$\n\\angle F E H+\\angle C M H=\\angle H G M+\\angle H G C=90^{\\circ}\n$$\n\nThus $C M \\perp E F$. Now, from the cyclic quadrilaterals $F I M B$ and EIMA, we get that\n\n$\\angle I F M=\\angle I B M$ and $\\angle I E M=\\angle I A M$. Therefore, the triangles $\\triangle E M F$ and $\\triangle A I B$ are similar, so $\\angle A J B=\\angle E M F$. Finally\n\n$$\n\\angle A I B=\\angle A I M+\\angle M I B=\\angle A E M+\\angle M F B=\\angle C A B+\\angle C B A\n$$\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":88,"cells":{"problem":{"kind":"string","value":"\nG5 ROU\n\nLet $A B C$ be an acute triangle with $A B \\neq A C$. The incircle $\\omega$ of the triangle touches the sides $B C, C A$ and $A B$ at $D, E$ and $F$, respectively. The perpendicular line erected at $C$ onto $B C$ meets $E F$ at $M$, and similarly, the perpendicular line erected at $B$ onto $B C$ meets $E F$ at $N$. The line $D M$ meets $\\omega$ again in $P$, and the line $D N$ meets $\\omega$ again at $Q$. Prove that $D P=D Q$.\n\n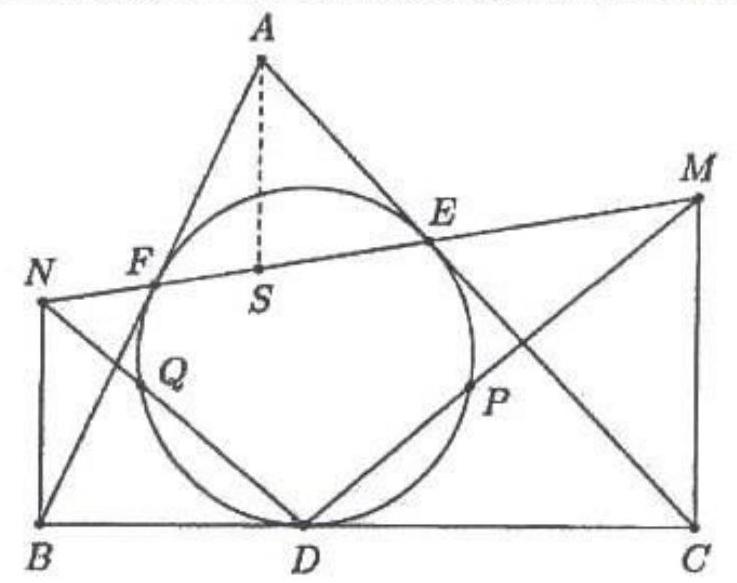![](https://cdn.mathpix.com/cropped/2024_06_05_07a1b610f48bd7c35addg-09.jpg?height=583&width=737&top_left_y=1595&top_left_x=607)\n\n"},"solution":{"kind":"string","value":"## Solution:\n\n## Proof 1.1.\n\nLet $\\{T\\}=E F \\cap B C$. Applying Menelaus' theorem to the triangle $A B C$ and the transversal line $E-F-T$ we obtain $\\frac{T B}{T C} \\cdot \\frac{E C}{E A} \\cdot \\frac{F A}{F B}=1$, i.e. $\\frac{T B}{T C} \\cdot \\frac{s-c}{s-a} \\cdot \\frac{s-a}{s-b}=1$, or $\\frac{T B}{T C}=\\frac{s-b}{s-c}$, where the notations are the usual ones.\n\nThis means that triangles $T B N$ and $T C M$ are similar, therefore $\\frac{T B}{T C}=\\frac{B N}{C M}$. From the above it follows $\\frac{B N}{C M}=\\frac{s-b}{s-c}, \\frac{B D}{C D}=\\frac{s-b}{s-c}$, and $\\angle D B N=\\angle D C M=90^{\\circ}$, which means that triangles $B D N$ and $C D M$ are similar, hence angles $B D N$ and $C D M$ are equal. This leads to the arcs $D Q$ and $D P$ being equal, and finally to $D P=D Q$.\n\n## Proof 1.2.\n\nLet $S$ be the meeting point of the altitude from $A$ with the line $E F$. Lines $B N, A S, C M$ are parallel, therefore triangles $B N F$ and $A S F$ are similar, as are triangles $A S E$ and $C M E$. We obtain $\\frac{B N}{A S}=\\frac{B F}{F A}$ and $\\frac{A S}{C M}=\\frac{A E}{E C}$.\n\nMultiplying the two relations, we obtain $\\frac{B N}{C M}=\\frac{B F}{F A} \\cdot \\frac{A E}{E C}=\\frac{B F}{E C}=\\frac{B D}{D C}$ (we have used that $A E=A F, B F=B D$ and $C E=C D)$.\n\nIt follows that the right triangles $B D N$ and $C D M$ are similar (SAS), which leads to the same ending as in the first proof.\n\n## NUMBER THEORY\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Geometry"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":89,"cells":{"problem":{"kind":"string","value":"\nNT1 SAU\n\nWhat is the greatest number of integers that can be selected from a set of 2015 consecutive numbers so that no sum of any two selected numbers is divisible by their difference?\n\n"},"solution":{"kind":"string","value":"## Solution:\n\nWe take any two chosen numbers. If their difference is 1 , it is clear that their sum is divisible by their difference. If their difference is 2 , they will be of the same parity, and their sum is divisible by their difference. Therefore, the difference between any chosen numbers will be at least 3 . In other words, we can choose at most one number of any three consecutive numbers. This implies that we can choose at most 672 numbers.\n\nNow, we will show that we can choose 672 such numbers from any 2015 consecutive numbers. Suppose that these numbers are $a, a+1, \\ldots, a+2014$. If $a$ is divisible by 3 , we can choose $a+1, a+4, \\ldots, a+2014$. If $a$ is not divisible by 3 , we can choose $a, a+3, \\ldots, a+$ 2013.\n"},"answer":{"kind":"string","value":"672"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"math-word-problem"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}},{"rowIdx":90,"cells":{"problem":{"kind":"string","value":"\nNT2 BUL\n\nA positive integer is called a repunit, if it is written only by ones. The repunit with $n$ digits will be denoted by $\\underbrace{11 \\ldots 1}_{n}$. Prove that:\n\na) the repunit $\\underbrace{11 \\ldots 1}_{n}$ is divisible by 37 if and only if $n$ is divisible by 3 ;\n\nb) there exists a positive integer $k$ such that the repunit $\\underbrace{11 \\ldots 1}_{n}$ is divisible by 41 if and only if $n$ is divisible by $k$.\n\n"},"solution":{"kind":"string","value":"## Solution:\n\na) Let $n=3 m+r$, where $m$ and $r$ are non-negative integers and $r<3$.\n\nDenote by $\\underbrace{00 \\ldots 0}_{p}$ a recording with $p$ zeroes and $\\underbrace{a b c a b c \\ldots a b c}_{p x a b c c}$ recording with $p$ times $a b c$. We\n\nhave: $\\quad \\underbrace{11 \\ldots 1}_{n}=\\underbrace{11 \\ldots 1}_{3 m+r}=\\underbrace{11 \\ldots 1}_{3 m} \\cdot \\underbrace{00 \\ldots 0}_{r}+\\underbrace{11 \\ldots 1}_{\\tau}=111 \\cdot \\underbrace{100100 \\ldots 100100 \\ldots 0}_{(m-1) \\times 100}+\\underbrace{11 \\ldots 1}_{r}$.\n\nSince $111=37.3$, the numbers $\\underbrace{11 \\ldots 1}_{n}$ and $\\underbrace{11 \\ldots 1}_{r}$ are equal modulo 37 . On the other hand the numbers 1 and 11 are not divisible by 37 . We conclude that $\\underbrace{11 \\ldots 1}_{n}$ is divisible by 37 if only if $r=0$, i.e. if and only if $n$ is divisible by 3 .\n\nb) Using the idea from a), we look for a repunit, which is divisible by 41 . Obviously, 1 and 11 are not divisible by 41 , while the residues of 111 and 1111 are 29 and 4 , respectively. We have $11111=41 \\cdot 271$. Since 11111 is a repunit with 5 digits, it follows in the same way as in a) that $\\underbrace{1}_{11 \\ldots 1}$ is divisible by 41 if and only if $n$ is divisible by 5 .\n\n"},"answer":{"kind":"string","value":"proof"},"problem_type":{"kind":"string","value":"Number Theory"},"question_type":{"kind":"string","value":"proof"},"problem_is_valid":{"kind":"string","value":"Yes"},"solution_is_valid":{"kind":"string","value":"Yes"},"source":{"kind":"string","value":"olympiads"},"synthetic":{"kind":"string","value":"false"}}}],"truncated":true},"paginationData":{"pageIndex":0,"numItemsPerPage":100,"numTotalItems":896215,"offset":0,"length":100}},"jwt":"eyJhbGciOiJFZERTQSJ9.eyJyZWFkIjp0cnVlLCJwZXJtaXNzaW9ucyI6eyJyZXBvLmNvbnRlbnQucmVhZCI6dHJ1ZX0sImlhdCI6MTc0MDE1Nzc2NSwic3ViIjoiL2RhdGFzZXRzL0FJLU1PL051bWluYU1hdGgtMS41IiwiZXhwIjoxNzQwMTYxMzY1LCJpc3MiOiJodHRwczovL2h1Z2dpbmdmYWNlLmNvIn0.60e04HFdn4xdNBalzpbXAtkTs0ycYnHKsbuw5jZ-PTFKkGymswloGMXyb59KxxGpkjHf9yM4NmqyppI4D3nNCg","displayUrls":true},"dataset":"AI-MO/NuminaMath-1.5","isGated":false,"isPrivate":false,"hasParquetFormat":true,"author":{"avatarUrl":"https://cdn-avatars.huggingface.co/v1/production/uploads/661d3f3e85f70e208d6f20db/kaXbnZDekN1gPzmRG_aFV.png","fullname":"Project-Numina","name":"AI-MO","type":"org","isHf":false,"isMod":false,"isEnterprise":true,"followerCount":248},"compact":true}"><div class="overflow-hidden px-2.5 mx-auto mb-10 rounded-lg border pt-2 shadow-sm "><div class="mb-2 flex flex-wrap items-center gap-2"><div class="mr-auto flex items-center"><svg class="mr-1 flex-none" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 12 12"><path fill="currentColor" d="M2.5 2h7a1 1 0 0 1 1 1v6a1 1 0 0 1-1 1h-7a1 1 0 0 1-1-1V3a1 1 0 0 1 1-1Zm0 2v2h3V4h-3Zm4 0v2h3V4h-3Zm-4 3v2h3V7h-3Zm4 0v2h3V7h-3Z"></path></svg> <div class="whitespace-nowrap font-semibold">Dataset Viewer</div> </div> <a href="/datasets/AI-MO/NuminaMath-1.5/tree/refs%2Fconvert%2Fparquet/default" class="group mr-1 text-xs text-gray-400 max-sm:hidden"><svg class="text-[.6rem] mr-1 inline -translate-y-px" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32"><path fill="currentColor" d="M12 10H6.78A11 11 0 0 1 27 16h2A13 13 0 0 0 6 7.68V4H4v8h8zm8 12h5.22A11 11 0 0 1 5 16H3a13 13 0 0 0 23 8.32V28h2v-8h-8z"></path></svg> <span class="underline decoration-gray-300 group-hover:decoration-gray-400 dark:decoration-gray-500 dark:group-hover:decoration-gray-300">Auto-converted</span> to Parquet </a> <button class="btn flex cursor-pointer items-center rounded border px-1 py-0.5 text-xs font-normal text-gray-700 shadow-sm hover:text-gray-800 hover:shadow dark:hover:text-gray-200"><svg class="mr-1.5" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32" style="transform: rotate(360deg);"><path d="M31 16l-7 7l-1.41-1.41L28.17 16l-5.58-5.59L24 9l7 7z" fill="currentColor"></path><path d="M1 16l7-7l1.41 1.41L3.83 16l5.58 5.59L8 23l-7-7z" fill="currentColor"></path><path d="M12.419 25.484L17.639 6l1.932.518L14.35 26z" fill="currentColor"></path></svg>API</button> <button class="btn flex cursor-pointer items-center rounded border px-1 py-0.5 text-xs font-normal text-gray-700 shadow-sm hover:text-gray-800 hover:shadow dark:hover:text-gray-200"><svg class="mr-1.5" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" fill="currentColor" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 12 12"><path d="M9.80603 2.86737H3.56107C3.37704 2.86737 3.20055 2.94048 3.07042 3.0706C2.94029 3.20073 2.86719 3.37723 2.86719 3.56126V9.80622C2.86719 9.99025 2.94029 10.1667 3.07042 10.2969C3.20055 10.427 3.37704 10.5001 3.56107 10.5001H9.80603C9.99006 10.5001 10.1666 10.427 10.2967 10.2969C10.4268 10.1667 10.4999 9.99025 10.4999 9.80622V3.56126C10.4999 3.37723 10.4268 3.20073 10.2967 3.0706C10.1666 2.94048 9.99006 2.86737 9.80603 2.86737Z" fill="currentColor" fill-opacity="0.3"></path><path fill-rule="evenodd" clip-rule="evenodd" d="M2.40942 1.66191C2.05175 1.66191 1.7618 1.95186 1.7618 2.30953V6.76191H1.43799V2.30953C1.43799 1.77303 1.87291 1.3381 2.40942 1.3381H6.45704V1.66191H2.40942Z" fill="currentColor"></path></svg>Embed</button> <a href="/datasets/AI-MO/NuminaMath-1.5/viewer/default/train" class="btn flex items-center rounded-full border px-2 py-0.5 text-xs font-normal text-gray-700 shadow-sm hover:text-gray-800 hover:shadow dark:hover:text-gray-200"><svg class="mr-1 text-red-500" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 12 12"><path fill="currentColor" d="M2.5 2h7a1 1 0 0 1 1 1v6a1 1 0 0 1-1 1h-7a1 1 0 0 1-1-1V3a1 1 0 0 1 1-1Zm0 2v2h3V4h-3Zm4 0v2h3V4h-3Zm-4 3v2h3V7h-3Zm4 0v2h3V7h-3Z"></path></svg> <div class="hidden sm:block">Full Screen Viewer</div> <div class="block sm:hidden">Full Screen</div></a></div> <div class="-mx-2.5 flex flex-nowrap border-t "><div class="grid flex-1 grid-cols-1 overflow-hidden text-sm md:grid-cols-2 md:place-content-center"><label class="relative block flex-1 px-3 py-2 hover:bg-gray-50 dark:border-gray-850 dark:hover:bg-gray-950 md:border-r md:border-r-0 hidden" title="default"><span class="text-gray-500">Subset (1)</span> <div class="flex items-center whitespace-nowrap"><span class="truncate">default</span> <span class="mx-2 text-gray-500">·</span> <span class="text-gray-500">896k rows</span> <svg class="ml-auto min-w-6 pl-2" width="1em" height="1em" viewBox="0 0 12 7" fill="none" xmlns="http://www.w3.org/2000/svg"><path d="M1 1L6 6L11 1" stroke="currentColor"></path></svg></div> <select class="absolute inset-0 z-10 w-full cursor-pointer border-0 bg-white text-base opacity-0"><optgroup label="Subset (1)"><option value="default" selected>default (896k rows)</option></optgroup></select></label> <label class="relative block flex-1 px-3 py-2 hover:bg-gray-50 dark:border-gray-850 dark:hover:bg-gray-900 md:border-r md:border-r" title="train"><div class="text-gray-500">Split (1)</div> <div class="flex items-center overflow-hidden whitespace-nowrap"><span class="truncate">train</span> <span class="mx-2 text-gray-500">·</span> <span class="text-gray-500">896k rows</span> <svg class="ml-auto min-w-6 pl-2" width="1em" height="1em" viewBox="0 0 12 7" fill="none" xmlns="http://www.w3.org/2000/svg"><path d="M1 1L6 6L11 1" stroke="currentColor"></path></svg></div> <select class="absolute inset-0 z-10 w-full cursor-pointer border-0 bg-white text-base opacity-0"><optgroup label="Split (1)"><option value="train" selected>train (896k rows)</option></optgroup></select></label></div> </div> <div class="relative -mx-2.5 flex items-center border-t bg-gradient-to-r text-smd dark:border-gray-900 dark:bg-gray-950 [&:has(:focus)]:from-gray-50 [&:has(:focus)]:to-transparent [&:has(:focus)]:to-20% dark:[&:has(:focus)]:from-gray-900"><form class="flex-1"><svg class="absolute left-3 top-1/2 transform -translate-y-1/2 pointer-events-none text-gray-400" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32"><path d="M30 28.59L22.45 21A11 11 0 1 0 21 22.45L28.59 30zM5 14a9 9 0 1 1 9 9a9 9 0 0 1-9-9z" fill="currentColor"></path></svg> <input disabled class="h-9 w-full border-none bg-transparent px-1 pl-9 pr-3 outline-none placeholder:text-gray-400 " placeholder="Search this dataset" dir="auto"></form> <div class="flex items-center gap-2 px-2 py-1"><button type="button" class="mr-2 flex items-center gap-1 rounded-md border border-yellow-200 bg-yellow-100 pl-0.5 pr-1 text-[.8rem] leading-normal text-gray-700 hover:bg-yellow-200/70 dark:border-orange-500/25 dark:bg-orange-500/20 dark:text-gray-300 dark:hover:brightness-110"><div class="rounded bg-yellow-300 px-1 font-mono text-[.7rem] font-bold text-black dark:bg-yellow-700 dark:text-gray-200">SQL </div> Console </button> </div></div> <div class="-mx-2.5 flex flex-1 flex-col overflow-hidden border-t min-h-64"> <div class="max-h-96 relative overflow-auto"><table class="w-full table-auto rounded-lg font-mono text-xs text-gray-900"><thead class="sticky left-0 right-0 top-0 z-1 bg-white align-top shadow-sm"><tr class="space-y-54 h-full min-w-fit divide-x border-b text-left"><th class="h-full max-w-sm p-2 text-left "><div class="flex h-full flex-col flex-nowrap justify-between"><div><div class="flex items-center justify-between">problem <form class="flex flex-col"><button id="asc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="-rotate-180 transform text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button> <button id="desc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button></form></div> <div class="mb-2 whitespace-nowrap text-xs font-normal text-gray-500"><span>string</span><span class="italic text-gray-400 before:mx-1 before:content-['·']">lengths</span></div></div> <div><div class="" style="height: 40px; padding-top: 2px"><svg width="130" height="28"><g><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="0" y="0" width="11.2" height="30" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="13.2" y="25" width="11.2" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="26.4" y="25" width="11.2" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="39.599999999999994" y="25" width="11.2" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="52.8" y="25" width="11.2" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="66" y="25" width="11.2" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="79.19999999999999" y="25" width="11.2" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="92.39999999999999" y="25" width="11.2" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="105.6" y="25" width="11.2" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="118.8" y="25" width="11.2" height="5" fill-opacity="1"></rect></g><rect class="fill-white dark:fill-gray-900" x="0" y="26" width="130" height="2" stroke-opacity="1"></rect><line class="stroke-gray-100 dark:stroke-gray-500/20" x1="0" y1="27.5" x2="130" y2="27.5" stroke-opacity="1"></line><g><rect class="fill-indigo-500 cursor-pointer" x="-1" y="0" width="13.2" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="12.2" y="0" width="13.2" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="25.4" y="0" width="13.2" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="38.599999999999994" y="0" width="13.2" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="51.8" y="0" width="13.2" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="65" y="0" width="13.2" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="78.19999999999999" y="0" width="13.2" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="91.39999999999999" y="0" width="13.2" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="104.6" y="0" width="13.2" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="117.8" y="0" width="13.2" height="30" fill-opacity="0"></rect></g></svg> <div class="relative font-light text-gray-400" style="height: 10px; width: 130px;"><div class="absolute left-0 overflow-hidden text-ellipsis whitespace-nowrap" style="max-width: 60px">0</div> <div class="absolute overflow-hidden text-ellipsis whitespace-nowrap" style="right: 0px; max-width: 60px">45.3k</div> </div></div></div></div></th><th class="h-full max-w-sm p-2 text-left "><div class="flex h-full flex-col flex-nowrap justify-between"><div><div class="flex items-center justify-between">solution <form class="flex flex-col"><button id="asc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="-rotate-180 transform text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button> <button id="desc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button></form></div> <div class="mb-2 whitespace-nowrap text-xs font-normal text-gray-500"><span>string</span><span class="italic text-gray-400 before:mx-1 before:content-['·']">lengths</span></div></div> <div><div class="" style="height: 40px; padding-top: 2px"><svg width="130" height="28"><g><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="0" y="0" width="10" height="30" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="12" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="24" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="36" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="48" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="60" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="72" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="84" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="96" y="26" width="10" height="4" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="108" y="25" width="10" height="5" fill-opacity="1"></rect><rect class=" fill-gray-200 dark:fill-gray-500/80" rx="2" x="120" y="24.996604682990686" width="10" height="5.003395317009312" fill-opacity="1"></rect></g><rect class="fill-white dark:fill-gray-900" x="0" y="26" width="130" height="2" stroke-opacity="1"></rect><line class="stroke-gray-100 dark:stroke-gray-500/20" x1="0" y1="27.5" x2="130" y2="27.5" stroke-opacity="1"></line><g><rect class="fill-indigo-500 cursor-pointer" x="-1" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="11" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="23" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="35" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="47" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="59" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="71" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="83" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="95" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="107" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-gray-200 cursor-pointer" x="119" y="0" width="12" height="30" fill-opacity="0"></rect></g></svg> <div class="relative font-light text-gray-400" style="height: 10px; width: 130px;"><div class="absolute left-0 overflow-hidden text-ellipsis whitespace-nowrap" style="max-width: 54px">0</div> <div class="absolute overflow-hidden text-ellipsis whitespace-nowrap" style="right: 12px; max-width: 54px">26.8k</div> <div class="absolute -translate-x-1/2" style="left: 125px">⌀</div></div></div></div></div></th><th class="h-full max-w-sm p-2 text-left "><div class="flex h-full flex-col flex-nowrap justify-between"><div><div class="flex items-center justify-between">answer <form class="flex flex-col"><button id="asc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="-rotate-180 transform text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button> <button id="desc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button></form></div> <div class="mb-2 whitespace-nowrap text-xs font-normal text-gray-500"><span>string</span><span class="italic text-gray-400 before:mx-1 before:content-['·']">lengths</span></div></div> <div><div class="" style="height: 40px; padding-top: 2px"><svg width="130" height="28"><g><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="0" y="0" width="10" height="30" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="12" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="24" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="36" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="48" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="60" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="72" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="84" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="96" y="25" width="10" height="5" fill-opacity="1"></rect><rect class="fill-gray-400 dark:fill-gray-500/80" rx="2" x="108" y="25" width="10" height="5" fill-opacity="1"></rect><rect class=" fill-gray-200 dark:fill-gray-500/80" rx="2" x="120" y="24.390732136643674" width="10" height="5.609267863356326" fill-opacity="1"></rect></g><rect class="fill-white dark:fill-gray-900" x="0" y="26" width="130" height="2" stroke-opacity="1"></rect><line class="stroke-gray-100 dark:stroke-gray-500/20" x1="0" y1="27.5" x2="130" y2="27.5" stroke-opacity="1"></line><g><rect class="fill-indigo-500 cursor-pointer" x="-1" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="11" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="23" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="35" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="47" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="59" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="71" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="83" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="95" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-indigo-500 cursor-pointer" x="107" y="0" width="12" height="30" fill-opacity="0"></rect><rect class="fill-gray-200 cursor-pointer" x="119" y="0" width="12" height="30" fill-opacity="0"></rect></g></svg> <div class="relative font-light text-gray-400" style="height: 10px; width: 130px;"><div class="absolute left-0 overflow-hidden text-ellipsis whitespace-nowrap" style="max-width: 54px">0</div> <div class="absolute overflow-hidden text-ellipsis whitespace-nowrap" style="right: 12px; max-width: 54px">575</div> <div class="absolute -translate-x-1/2" style="left: 125px">⌀</div></div></div></div></div></th><th class="h-full max-w-sm p-2 text-left "><div class="flex h-full flex-col flex-nowrap justify-between"><div><div class="flex items-center justify-between">problem_type <form class="flex flex-col"><button id="asc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="-rotate-180 transform text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button> <button id="desc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button></form></div> <div class="mb-2 whitespace-nowrap text-xs font-normal text-gray-500"><span>string</span><span class="italic text-gray-400 before:mx-1 before:content-['·']">classes</span></div></div> <div><div class="" style="height: 40px; padding-top: 2px"><svg width="130" height="28"><defs><clipPath id="rounded-bar"><rect x="0" y="0" width="130" height="8" rx="4"></rect></clipPath><pattern id="hatching" patternUnits="userSpaceOnUse" patternTransform="rotate(-45)" height="1" width="5"><line y1="0" class="stroke-gray-400 dark:stroke-gray-500/80" stroke-width="3" y2="1" x1="2" x2="2"></line></pattern><pattern id="hatching-faded" patternUnits="userSpaceOnUse" patternTransform="rotate(-45)" height="1" width="5"><line y1="0" class="stroke-gray-100 dark:stroke-gray-500/20" stroke-width="3" y2="1" x1="2" x2="2"></line></pattern></defs><g height="8" style="transform: translateY(20px)" clip-path="url(#rounded-bar)"><g style="transform: scaleX(1.0153846153846153) translateX(-1px)"><g><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="1" y="0" width="59.34571503489676" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="62.34571503489676" y="0" width="24.660433043410343" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="89.0061480783071" y="0" width="11.255513464960975" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="102.26166154326808" y="0" width="8.682247005461859" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="112.94390854872994" y="0" width="4.054719012736899" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="118.99862756146683" y="0" width="3.4991603577266615" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="124.4977879191935" y="0" width="1.9113940293344789" height="8" fill-opacity="1"></rect></g></g></g><g style="transform: scaleX(1.0153846153846153) translateX(-1px)"><g><rect class="fill-white cursor-pointer" x="0" y="0" width="61.34571503489676" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="61.34571503489676" y="0" width="26.660433043410343" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="88.0061480783071" y="0" width="13.255513464960975" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="101.26166154326808" y="0" width="10.682247005461859" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="111.94390854872994" y="0" width="6.054719012736899" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="117.99862756146683" y="0" width="5.4991603577266615" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="123.4977879191935" y="0" width="3.911394029334479" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="127.40918194852797" y="0" width="1.8342138884084735" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="129.24339583693646" y="0" width="0.7566041630635506" height="28" fill-opacity="0"></rect></g></g></svg> <div class="relative font-light text-gray-400" style="height: 10px; width: 130px;"><div class="absolute left-0 max-w-full overflow-hidden text-ellipsis whitespace-nowrap">9 values</div></div></div></div></div></th><th class="h-full max-w-sm p-2 text-left "><div class="flex h-full flex-col flex-nowrap justify-between"><div><div class="flex items-center justify-between">question_type <form class="flex flex-col"><button id="asc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="-rotate-180 transform text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button> <button id="desc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button></form></div> <div class="mb-2 whitespace-nowrap text-xs font-normal text-gray-500"><span>string</span><span class="italic text-gray-400 before:mx-1 before:content-['·']">classes</span></div></div> <div><div class="" style="height: 40px; padding-top: 2px"><svg width="130" height="28"><defs><clipPath id="rounded-bar"><rect x="0" y="0" width="130" height="8" rx="4"></rect></clipPath><pattern id="hatching" patternUnits="userSpaceOnUse" patternTransform="rotate(-45)" height="1" width="5"><line y1="0" class="stroke-gray-400 dark:stroke-gray-500/80" stroke-width="3" y2="1" x1="2" x2="2"></line></pattern><pattern id="hatching-faded" patternUnits="userSpaceOnUse" patternTransform="rotate(-45)" height="1" width="5"><line y1="0" class="stroke-gray-100 dark:stroke-gray-500/20" stroke-width="3" y2="1" x1="2" x2="2"></line></pattern></defs><g height="8" style="transform: translateY(20px)" clip-path="url(#rounded-bar)"><g style="transform: scaleX(1.0153846153846153) translateX(-1px)"><g><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="1" y="0" width="89.60509475962799" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="92.60509475962799" y="0" width="19.24308341190451" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="113.8481781715325" y="0" width="14.100757072800612" height="8" fill-opacity="1"></rect></g></g></g><g style="transform: scaleX(1.0153846153846153) translateX(-1px)"><g><rect class="fill-white cursor-pointer" x="0" y="0" width="91.60509475962799" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="91.60509475962799" y="0" width="21.24308341190451" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="112.8481781715325" y="0" width="16.10075707280061" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="128.94893524433311" y="0" width="0.7566041630635506" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="129.70553940739666" y="0" width="0.29446059260333735" height="28" fill-opacity="0"></rect></g></g></svg> <div class="relative font-light text-gray-400" style="height: 10px; width: 130px;"><div class="absolute left-0 max-w-full overflow-hidden text-ellipsis whitespace-nowrap">5 values</div></div></div></div></div></th><th class="h-full max-w-sm p-2 text-left "><div class="flex h-full flex-col flex-nowrap justify-between"><div><div class="flex items-center justify-between">problem_is_valid <form class="flex flex-col"><button id="asc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="-rotate-180 transform text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button> <button id="desc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button></form></div> <div class="mb-2 whitespace-nowrap text-xs font-normal text-gray-500"><span>string</span><span class="italic text-gray-400 before:mx-1 before:content-['·']">classes</span></div></div> <div><div class="" style="height: 40px; padding-top: 2px"><svg width="130" height="28"><defs><clipPath id="rounded-bar"><rect x="0" y="0" width="130" height="8" rx="4"></rect></clipPath><pattern id="hatching" patternUnits="userSpaceOnUse" patternTransform="rotate(-45)" height="1" width="5"><line y1="0" class="stroke-gray-400 dark:stroke-gray-500/80" stroke-width="3" y2="1" x1="2" x2="2"></line></pattern><pattern id="hatching-faded" patternUnits="userSpaceOnUse" patternTransform="rotate(-45)" height="1" width="5"><line y1="0" class="stroke-gray-100 dark:stroke-gray-500/20" stroke-width="3" y2="1" x1="2" x2="2"></line></pattern></defs><g height="8" style="transform: translateY(20px)" clip-path="url(#rounded-bar)"><g style="transform: scaleX(1.0153846153846153) translateX(-1px)"><g><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="1" y="0" width="122.65343695430226" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="125.65343695430226" y="0" width="2.40631991207467" height="8" fill-opacity="1"></rect></g></g></g><g style="transform: scaleX(1.0153846153846153) translateX(-1px)"><g><rect class="fill-white cursor-pointer" x="0" y="0" width="124.65343695430226" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="124.65343695430226" y="0" width="4.40631991207467" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="129.05975686637694" y="0" width="0.7570393265008954" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="129.81679619287783" y="0" width="0.1602851994220137" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="129.97708139229985" y="0" width="0.022918607700161235" height="28" fill-opacity="0"></rect></g></g></svg> <div class="relative font-light text-gray-400" style="height: 10px; width: 130px;"><div class="absolute left-0 max-w-full overflow-hidden text-ellipsis whitespace-nowrap">5 values</div></div></div></div></div></th><th class="h-full max-w-sm p-2 text-left "><div class="flex h-full flex-col flex-nowrap justify-between"><div><div class="flex items-center justify-between">solution_is_valid <form class="flex flex-col"><button id="asc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="-rotate-180 transform text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button> <button id="desc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button></form></div> <div class="mb-2 whitespace-nowrap text-xs font-normal text-gray-500"><span>string</span><span class="italic text-gray-400 before:mx-1 before:content-['·']">classes</span></div></div> <div><div class="" style="height: 40px; padding-top: 2px"><svg width="130" height="28"><defs><clipPath id="rounded-bar"><rect x="0" y="0" width="130" height="8" rx="4"></rect></clipPath><pattern id="hatching" patternUnits="userSpaceOnUse" patternTransform="rotate(-45)" height="1" width="5"><line y1="0" class="stroke-gray-400 dark:stroke-gray-500/80" stroke-width="3" y2="1" x1="2" x2="2"></line></pattern><pattern id="hatching-faded" patternUnits="userSpaceOnUse" patternTransform="rotate(-45)" height="1" width="5"><line y1="0" class="stroke-gray-100 dark:stroke-gray-500/20" stroke-width="3" y2="1" x1="2" x2="2"></line></pattern></defs><g height="8" style="transform: translateY(20px)" clip-path="url(#rounded-bar)"><g style="transform: scaleX(1.0153846153846153) translateX(-1px)"><g><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="1" y="0" width="120.56929419837874" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="123.56929419837874" y="0" width="2.717461769776225" height="8" fill-opacity="1"></rect></g></g></g><g style="transform: scaleX(1.0153846153846153) translateX(-1px)"><g><rect class="fill-white cursor-pointer" x="0" y="0" width="122.56929419837874" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="122.56929419837874" y="0" width="4.717461769776225" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="127.28675596815496" y="0" width="1.950402526179544" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="129.2371584943345" y="0" width="0.758199762333815" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="129.9953582566683" y="0" width="0.004641743331678224" height="28" fill-opacity="0"></rect></g></g></svg> <div class="relative font-light text-gray-400" style="height: 10px; width: 130px;"><div class="absolute left-0 max-w-full overflow-hidden text-ellipsis whitespace-nowrap">5 values</div></div></div></div></div></th><th class="h-full max-w-sm p-2 text-left "><div class="flex h-full flex-col flex-nowrap justify-between"><div><div class="flex items-center justify-between">source <form class="flex flex-col"><button id="asc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="-rotate-180 transform text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button> <button id="desc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button></form></div> <div class="mb-2 whitespace-nowrap text-xs font-normal text-gray-500"><span>string</span><span class="italic text-gray-400 before:mx-1 before:content-['·']">classes</span></div></div> <div><div class="" style="height: 40px; padding-top: 2px"><svg width="130" height="28"><defs><clipPath id="rounded-bar"><rect x="0" y="0" width="130" height="8" rx="4"></rect></clipPath><pattern id="hatching" patternUnits="userSpaceOnUse" patternTransform="rotate(-45)" height="1" width="5"><line y1="0" class="stroke-gray-400 dark:stroke-gray-500/80" stroke-width="3" y2="1" x1="2" x2="2"></line></pattern><pattern id="hatching-faded" patternUnits="userSpaceOnUse" patternTransform="rotate(-45)" height="1" width="5"><line y1="0" class="stroke-gray-100 dark:stroke-gray-500/20" stroke-width="3" y2="1" x1="2" x2="2"></line></pattern></defs><g height="8" style="transform: translateY(20px)" clip-path="url(#rounded-bar)"><g style="transform: scaleX(1.0153846153846153) translateX(-1px)"><g><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="1" y="0" width="36.99340002120027" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="39.99340002120027" y="0" width="26.587916961889725" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="68.58131698309" y="0" width="20.03870722984998" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="90.62002421293998" y="0" width="19.571341698141627" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="112.1913659110816" y="0" width="7.840640917636952" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="122.03200682871855" y="0" width="2.343511322617899" height="8" fill-opacity="1"></rect></g></g></g><g style="transform: scaleX(1.0153846153846153) translateX(-1px)"><g><rect class="fill-white cursor-pointer" x="0" y="0" width="38.99340002120027" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="38.99340002120027" y="0" width="28.587916961889725" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="67.58131698309" y="0" width="22.03870722984998" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="89.62002421293998" y="0" width="21.571341698141627" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="111.1913659110816" y="0" width="9.840640917636952" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="121.03200682871855" y="0" width="4.343511322617899" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="125.37551815133645" y="0" width="1.597630032971999" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="126.97314818430846" y="0" width="1.0609284602467042" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="128.03407664455517" y="0" width="0.8517599013629542" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="128.88583654591812" y="0" width="0.5864552590617207" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="129.47229180497985" y="0" width="0.5277081950201681" height="28" fill-opacity="0"></rect></g></g></svg> <div class="relative font-light text-gray-400" style="height: 10px; width: 130px;"><div class="absolute left-0 max-w-full overflow-hidden text-ellipsis whitespace-nowrap">11 values</div></div></div></div></div></th><th class="h-full max-w-sm p-2 text-left "><div class="flex h-full flex-col flex-nowrap justify-between"><div><div class="flex items-center justify-between">synthetic <form class="flex flex-col"><button id="asc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="-rotate-180 transform text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button> <button id="desc" class="-mr-1 ml-2 h-[0.4rem] w-[0.8rem] transition ease-in-out"><svg class="text-gray-300 hover:text-gray-500" xmlns="http://www.w3.org/2000/svg" viewBox="0 64 256 128" fill="currentColor" aria-hidden="true"><path d="M213.65674,101.657l-80,79.99976a7.99945,7.99945,0,0,1-11.31348,0l-80-79.99976A8,8,0,0,1,48,88H208a8,8,0,0,1,5.65674,13.657Z"></path></svg></button></form></div> <div class="mb-2 whitespace-nowrap text-xs font-normal text-gray-500"><span>bool</span></div></div> <div><div class="" style="height: 40px; padding-top: 2px"><svg width="130" height="28"><defs><clipPath id="rounded-bar"><rect x="0" y="0" width="130" height="8" rx="4"></rect></clipPath><pattern id="hatching" patternUnits="userSpaceOnUse" patternTransform="rotate(-45)" height="1" width="5"><line y1="0" class="stroke-gray-400 dark:stroke-gray-500/80" stroke-width="3" y2="1" x1="2" x2="2"></line></pattern><pattern id="hatching-faded" patternUnits="userSpaceOnUse" patternTransform="rotate(-45)" height="1" width="5"><line y1="0" class="stroke-gray-100 dark:stroke-gray-500/20" stroke-width="3" y2="1" x1="2" x2="2"></line></pattern></defs><g height="8" style="transform: translateY(20px)" clip-path="url(#rounded-bar)"><g style="transform: scaleX(1.0153846153846153) translateX(-1px)"><g><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="1" y="0" width="82.7923210390364" height="8" fill-opacity="1"></rect><rect class="fill-indigo-500 dark:fill-indigo-600/80" x="85.7923210390364" y="0" width="43.207678960963605" height="8" fill-opacity="1"></rect></g></g></g><g style="transform: scaleX(1.0153846153846153) translateX(-1px)"><g><rect class="fill-white cursor-pointer" x="0" y="0" width="84.7923210390364" height="28" fill-opacity="0"></rect><rect class="fill-white cursor-pointer" x="84.7923210390364" y="0" width="45.207678960963605" height="28" fill-opacity="0"></rect></g></g></svg> <div class="relative font-light text-gray-400" style="height: 10px; width: 130px;"><div class="absolute left-0 max-w-full overflow-hidden text-ellipsis whitespace-nowrap">2 classes</div></div></div></div></div></th></tr></thead> <tbody class="h-16 overflow-scroll"><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="0"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 1. Find all prime numbers $p$ for which there exist positive integers $x, y$ and $z$ such that the number $$ x^{p}+y^{p}+z^{p}-x-y-z $$ is a product of exactly three distinct prime numbers. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Let $A=x^{p}+y^{p}+z^{p}-x-y-z$. For $p=2$, we take $x=y=4$ and $z=3$. Then $A=30=2 \cdot 3 \cdot 5$. For $p=3$ we can take $x=3$ and $y=2$ and $z=1$. Then again $A=30=2 \cdot 3 \cdot 5$. For $p=5$ we can take $x=2$ and $y=1$ and $z=1$. Again $A=30=2 \cdot 3 \cdot 5$. Assume now that $p \geqslant 7$. Working modulo 2 and modulo 3 we see that $A$ is divisible by both 2 and 3. Moreover, by Fermat's Little Theorem, we have $$ x^{p}+y^{p}+z^{p}-x-y-z \equiv x+y+z-x-y-z=0 \bmod p \text {. } $$ Therefore, by the given condition, we have to solve the equation $$ x^{p}+y^{p}+z^{p}-x-y-z=6 p $$ If one of the numbers $x, y$ and $z$ is bigger than or equal to 2 , let's say $x \geqslant 2$, then $$ 6 p \geqslant x^{p}-x=x\left(x^{p-1}-1\right) \geqslant 2\left(2^{p-1}-1\right)=2^{p}-2 $$ It is easy to check by induction that $2^{n}-2>6 n$ for all natural numbers $n \geqslant 6$. This contradiction shows that there are no more values of $p$ which satisfy the required property. Remark. There are a couple of other ways to prove that $2^{p}-2>6 p$ for $p \geqslant 7$. For example, we can use the Binomial Theorem as follows: $$ 2^{p}-2 \geqslant 1+p+\frac{p(p-1)}{2}+\frac{p(p-1)(p-2)}{6}-2 \geqslant 1+p+3 p+5 p-2>6 p $$ We can also use Bernoulli's Inequality as follows: $$ 2^{p}-2=8(1+1)^{p-3}-2 \geqslant 8(1+(p-3))-2=8 p-18>6 p $$ The last inequality is true for $p \geqslant 11$. For $p=7$ we can see directly that $2^{p}-2>6 p$. One can also use calculus to show that $f(x)=2^{x}-6 x$ is increasing for $x \geqslant 5$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="1"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 2. Let $a, b$ be two distinct real numbers and let $c$ be a positive real number such that $$ a^{4}-2019 a=b^{4}-2019 b=c . $$ Prove that $-\sqrt{c}<a b<0$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Firstly, we see that $$ 2019(a-b)=a^{4}-b^{4}=(a-b)(a+b)\left(a^{2}+b^{2}\right) $$ Since $a \neq b$, we get $(a+b)\left(a^{2}+b^{2}\right)=2019$, so $a+b \neq 0$. Thus $$ \begin{aligned} 2 c & =a^{4}-2019 a+b^{4}-2019 b \\ & =a^{4}+b^{4}-2019(a+b) \\ & =a^{4}+b^{4}-(a+b)^{2}\left(a^{2}+b^{2}\right) \\ & =-2 a b\left(a^{2}+a b+b^{2}\right) \end{aligned} $$ Hence $a b\left(a^{2}+a b+b^{2}\right)=-c0 $$ thus $a b-a b$ (the equality does not occur since $a+b \neq 0$ ). So $$ -c=a b\left(a^{2}+a b+b^{2}\right)<-(a b)^{2} \Longrightarrow(a b)^{2}<c \Rightarrow-\sqrt{c}<a b<\sqrt{c} $$ Therefore, we have $-\sqrt{c}<a b<0$. Remark. We can get $c=-a b\left(a^{2}+a b+b^{2}\right)$ in several other ways. For example using that, $$ (a-b) c=a\left(b^{4}-2019 b\right)-b\left(a^{4}-2019 a\right)=a b\left(b^{3}-a^{3}\right)=a b(b-a)\left(a^{2}+a b+b^{2}\right) $$ We can also divide $f(x)=x^{4}-2019 x-c$ by $(x-a)(x-b)$ and look at the constant term of the remainder. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Algebra</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Incomplete</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="2"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 3. Triangle $A B C$ is such that $A B<A C$. The perpendicular bisector of side $B C$ intersects lines $A B$ and $A C$ at points $P$ and $Q$, respectively. Let $H$ be the orthocentre of triangle $A B C$, and let $M$ and $N$ be the midpoints of segments $B C$ and $P Q$, respectively. Prove that lines $H M$ and $A N$ meet on the circumcircle of $A B C$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. We have $$ \angle A P Q=\angle B P M=90^{\circ}-\angle M B P=90^{\circ}-\angle C B A=\angle H C B $$ and $$ \angle A Q P=\angle M Q C=90^{\circ}-\angle Q C M=90^{\circ}-\angle A C B=\angle C B H $$ From these two equalities, we see that the triangles $A P Q$ and $H C B$ are similar. Moreover, since $M$ and $N$ are the midpoints of the segments $B C$ and $P Q$ respectively, then the triangles $A Q N$ and $H B M$ are also similar. Therefore, we have $\angle A N Q=\angle H M B$. ![](https://cdn.mathpix.com/cropped/2024_06_05_fe2687448771fc19bd4eg-4.jpg?height=883&width=545&top_left_y=865&top_left_x=779) Let $L$ be the intersection of $A N$ and $H M$. We have $$ \angle M L N=180^{\circ}-\angle L N M-\angle N M L=180^{\circ}-\angle L M B-\angle N M L=180^{\circ}-\angle N M B=90^{\circ} . $$ Now let $D$ be the point on the circumcircle of $A B C$ diametrically oposite to $A$. It is known that $D$ is also the relfection of point $H$ over the point $M$. Therefore, we have that $D$ belongs on $M H$ and that $\angle D L A=\angle M L A=\angle M L N=90^{\circ}$. But, as $D A$ is the diameter of the circumcirle of $A B C$, the condition that $\angle D L A=90^{\circ}$ is enough to conclude that $L$ belongs on the circumcircle of $A B C$. Remark. There is a spiral similarity mapping $A Q P$ to $H B C$. Since the similarity maps $A N$ to $H M$, it also maps $A H$ to $N M$, and since these two lines are parallel, the centre of the similarity is $L=A N \cap H M$. Since the similarity maps $B C$ to $Q P$, its centre belongs on the circumcircle of $B C X$, where $X=B Q \cap P C$. But $X$ is the reflection of $A$ on $Q M$ and so it must belong on the circumcircle of $A B C$. Hence so must $L$. Remark. Students have also submitted correct proofs using radical axes, harmonic quadruples, coordinate geometry and complex numbers. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="3"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 4. A $5 \times 100$ table is divided into 500 unit square cells, where $n$ of them are coloured black and the rest are coloured white. Two unit square cells are called adjacent if they share a common side. Each of the unit square cells has at most two adjacent black unit square cells. Find the largest possible value of $n$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. If we colour all the cells along all edges of the board together with the entire middle row except the second and the last-but-one cell, the condition is satisfied and there are 302 black cells. The figure below exhibits this colouring for the $5 \times 8$ case. ![](https://cdn.mathpix.com/cropped/2024_06_05_fe2687448771fc19bd4eg-5.jpg?height=320&width=493&top_left_y=629&top_left_x=816) We can cover the table by one fragment like the first one on the figure below, 24 fragments like the middle one, and one fragment like the third one. ![](https://cdn.mathpix.com/cropped/2024_06_05_fe2687448771fc19bd4eg-5.jpg?height=317&width=737&top_left_y=1132&top_left_x=694) In each fragment, among the cells with the same letter, there are at most two coloured black, so the total number of coloured cells is at most $(5+24 \cdot 6+1) \cdot 2+2=302$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">302</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="4"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 1. A trapezoid $A B C D(A B \| C D, A B>C D)$ is circumscribed. The incircle of the triangle $A B C$ touches the lines $A B$ and $A C$ at the points $M$ and $N$, respectively. Prove that the incenter of the trapezoid $A B C D$ lies on the line $M N$. ![](https://cdn.mathpix.com/cropped/2024_06_05_bc5716af31e6d23d397cg-1.jpg?height=437&width=643&top_left_y=752&top_left_x=661) </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution. Version 1. Let $I$ be the incenter of triangle $A B C$ and $R$ be the common point of the lines $B I$ and $M N$. Since $$ m(\widehat{A N M})=90^{\circ}-\frac{1}{2} m(\widehat{M A N}) \quad \text { and } \quad m(\widehat{B I C})=90^{\circ}+\frac{1}{2} m(\widehat{M A N}) $$ the quadrilateral $I R N C$ is cyclic. It follows that $m(\widehat{B R C})=90^{\circ}$ and therefore $$ m(\widehat{B C R})=90^{\circ}-m(\widehat{C B R})=90^{\circ}-\frac{1}{2}\left(180^{\circ}-m(\widehat{B C D})\right)=\frac{1}{2} m(\widehat{B C D}) $$ So, $(C R$ is the angle bisector of $\widehat{D C B}$ and $R$ is the incenter of the trapezoid. Version 2. If $R$ is the incentre of the trapezoid $A B C D$, then $B, I$ and $R$ are collinear, and $m(\widehat{B R C})=90^{\circ}$. The quadrilateral $I R N C$ is cyclic. Then $m(\widehat{M N C})=90^{\circ}+\frac{1}{2} \cdot m(\widehat{B A C})$ and $m(\widehat{R N C})=m(\widehat{B I C})=90^{\circ}+\frac{1}{2} \cdot m(\widehat{B A C})$, so that $m(\widehat{M N C})=m(\widehat{R N C})$ and the points $M, R$ and $N$ are collinear. Version 3. If $R$ is the incentre of the trapezoid $A B C D$, let $M^{\prime} \in(A B)$ and $N^{\prime} \in(A C)$ be the unique points, such that $R \in M^{\prime} N^{\prime}$ and $\left(A M^{\prime}\right) \equiv\left(A N^{\prime}\right)$. Let $S$ be the intersection point of $C R$ and $A B$. Then $C R=R S$. Consider $K \in A C$ such that $S K \| M^{\prime} N^{\prime}$. Then $N^{\prime}$ is the midpoint of $(C K)$. We deduce $$ A N^{\prime}=\frac{A K+A C}{2}=\frac{A S+A C}{2}=\frac{A B-B S+A C}{2}=\frac{A B+A C-B C}{2}=A N $$ We conclude that $N=N^{\prime}$, hence $M=M^{\prime}$, and $R, M, N$ are collinear. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="5"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 2. Let $a, b$ and $c$ be positive real numbers. Prove that $$ \frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+\frac{8}{(c+a)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3} $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Since $2 a b \leq a^{2}+b^{2}$, it follows that $(a+b)^{2} \leq 2\left(a^{2}+b^{2}\right)$ and $4 a b c \leq 2 c\left(a^{2}+b^{2}\right)$, for any positive reals $a, b, c$. Adding these inequalities, we find $$ (a+b)^{2}+4 a b c \leq 2\left(a^{2}+b^{2}\right)(c+1) $$ so that $$ \frac{8}{(a+b)^{2}+4 a b c} \geq \frac{4}{\left(a^{2}+b^{2}\right)(c+1)} $$ Using the AM-GM inequality, we have $$ \frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq 2 \sqrt{\frac{2}{c+1}}=\frac{4}{\sqrt{2(c+1)}} $$ respectively $$ \frac{c+3}{8}=\frac{(c+1)+2}{8} \geq \frac{\sqrt{2(c+1)}}{4} $$ We conclude that $$ \frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq \frac{8}{c+3} $$ and finally $$ \frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(a+c)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3} $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="6"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 3. Find all the triples of integers $(a, b, c)$ such that the number $$ N=\frac{(a-b)(b-c)(c-a)}{2}+2 $$ is a power of 2016 . (A power of 2016 is an integer of the form $2016^{n}$, where $n$ is a non-negative integer.) </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Let $a, b, c$ be integers and $n$ be a positive integer such that $$ (a-b)(b-c)(c-a)+4=2 \cdot 2016^{n} $$ We set $a-b=-x, b-c=-y$ and we rewrite the equation as $$ x y(x+y)+4=2 \cdot 2016^{n} $$ If $n>0$, then the right hand side is divisible by 7 , so we have that $$ x y(x+y)+4 \equiv 0 \quad(\bmod 7) $$ or $$ 3 x y(x+y) \equiv 2 \quad(\bmod 7) $$ or $$ (x+y)^{3}-x^{3}-y^{3} \equiv 2 \quad(\bmod 7) $$ Note that, by Fermat's Little Theorem, for any integer $k$ the cubic residues are $k^{3} \equiv-1,0,1$ $(\bmod 7)$. It follows that in (1) some of $(x+y)^{3}, x^{3}$ and $y^{3}$ should be divisible by 7 . But in this case, $x y(x+y)$ is divisible by 7 and this is a contradiction. So, the only possibility is to have $n=0$ and consequently, $x y(x+y)+4=2$, or, equivalently, $x y(x+y)=-2$. The solutions for this are $(x, y) \in\{(-1,-1),(2,-1),(-1,2)\}$, so the required triples are $(a, b, c)=(k+2, k+1, k), k \in \mathbb{Z}$, and all their cyclic permutations. (9) Alternative version: If $n>0$ then 9 divides $(a-b)(b-c)(c-a)+4$, that is, the equation $x y(x+y)+4 \equiv 0(\bmod 9))$ has the solution $x=b-a, y=c-b$. But then $x$ and $y$ have to be 1 modulo 3 , implying $x y(x+y) \equiv 2(\bmod 9)$, which is a contradiction. We can continue now as in the first version. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">(,b,)=(k+2,k+1,k),k\in\mathbb{Z}</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="7"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 2. Let $n$ three-digit numbers satisfy the following properties: (1) No number contains the digit 0 . (2) The sum of the digits of each number is 9 . (3) The units digits of any two numbers are different. (4) The tens digits of any two numbers are different. (5) The hundreds digits of any two numbers are different. Find the largest possible value of $n$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Let $S$ denote the set of three-digit numbers that have digit sum equal to 9 and no digit equal to 0 . We will first find the cardinality of $S$. We start from the number 111 and each element of $S$ can be obtained from 111 by a string of 6 A's (which means that we add 1 to the current digit) and $2 G$ 's (which means go to the next digit). Then for example 324 can be obtained from 111 by the string AAGAGAAA. There are in total $$ \frac{8!}{6!\cdot 2!}=28 $$ such words, so $S$ contains 28 numbers. Now, from the conditions (3), (4), (5), if $\overline{a b c}$ is in $T$ then each of the other numbers of the form $\overline{* c}$ cannot be in $T$, neither $\overline{* *}$ can be, nor $\overline{a * *}$. Since there are $a+b-2$ numbers of the first category, $a+c-2$ from the second and $b+c-2$ from the third one. In these three categories there are $$ (a+b-2)+(b+c-2)+(c+a-2)=2(a+b+c)-6=2 \cdot 9-6=12 $$ distinct numbers that cannot be in $T$ if $\overline{a b c}$ is in $T$. So, if $T$ has $n$ numbers, then $12 n$ are the forbidden ones that are in $S$, but each number from $S$ can be a forbidden number no more than three times, once for each of its digits, so $$ n+\frac{12 n}{3} \leq 28 \Longleftrightarrow n \leq \frac{28}{5} $$ and since $n$ is an integer, we get $n \leq 5$. A possible example for $n=5$ is $$ T=\{144,252,315,423,531\} $$ Comment by PSC. It is classical to compute the cardinality of $S$ and this can be done in many ways. In general, the number of solutions of the equation $$ x_{1}+x_{2}+\cdots+x_{k}=n $$ in positive integers, where the order of $x_{i}$ matters, is well known that equals to $\binom{n-1}{k-1}$. In our case, we want to count the number of positive solutions to $a+b+c=9$. By the above, this equals to $\binom{9-1}{3-1}=28$. Using the general result above, we can also find that there are $a+b-2$ numbers of the form $\overline{* c}$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">5</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="8"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 4. Let $A B C$ be an acute triangle, $A^{\prime}, B^{\prime}$ and $C^{\prime}$ be the reflections of the vertices $A, B$ and $C$ with respect to $B C, C A$, and $A B$, respectively, and let the circumcircles of triangles $A B B^{\prime}$ and $A C C^{\prime}$ meet again at $A_{1}$. Points $B_{1}$ and $C_{1}$ are defined similarly. Prove that the lines $A A_{1}, B B_{1}$ and $C C_{1}$ have a common point. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Let $O_{1}, O_{2}$ and $O$ be the circumcenters of triangles $A B B^{\prime}, A C C^{\prime}$ and $A B C$ respectively. As $A B$ is the perpendicular bisector of the line segment $C C^{\prime}, O_{2}$ is the intersection of the perpendicular bisector of $A C$ with $A B$. Similarly, $O_{1}$ is the intersection of the perpendicular bisector of $A B$ with $A C$. It follows that $O$ is the orthocenter of triangle $A O_{1} O_{2}$. This means that $A O$ is perpendicular to $O_{1} O_{2}$. On the other hand, the segment $A A_{1}$ is the common chord of the two circles, thus it is perpendicular to $O_{1} O_{2}$. As a result, $A A_{1}$ passes through $O$. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent at $O$. ![](https://cdn.mathpix.com/cropped/2024_06_05_9020024f2910a9287423g-4.jpg?height=897&width=1087&top_left_y=820&top_left_x=497) Comment by PSC. We present here a different approach. We first prove that $A_{1}, B$ and $C^{\prime}$ are collinear. Indeed, since $\angle B A B^{\prime}=\angle C A C^{\prime}=2 \angle B A C$, then from the circles $\left(A B B^{\prime}\right),\left(A C C^{\prime}\right)$ we get $$ \angle A A_{1} B=\frac{\angle B A_{1} B^{\prime}}{2}=\frac{180^{\circ}-\angle B A B^{\prime}}{2}=90^{\circ}-\angle B A C=\angle A A_{1} C^{\prime} $$ It follows that $$ \angle A_{1} A C=\angle A_{1} C^{\prime} C=\angle B C^{\prime} C=90^{\circ}-\angle A B C $$ On the other hand, if $O$ is the circumcenter of $A B C$, then $$ \angle O A C=90^{\circ}-\angle A B C \text {. } $$ From (1) and (2) we conclude that $A_{1}, A$ and $O$ are collinear. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent in $O$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="9"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"># Problem 1 Let $a, b$ and $c$ be positive real numbers such that $a+b+c=1$. Prove that $$ \frac{a}{b}+\frac{b}{a}+\frac{b}{c}+\frac{c}{b}+\frac{c}{a}+\frac{a}{c}+6 \geq 2 \sqrt{2}\left(\sqrt{\frac{1-a}{a}}+\sqrt{\frac{1-b}{b}}+\sqrt{\frac{1-c}{c}}\right) $$ When does equality hold? </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution Replacing $1-a, 1-b, 1-c$ with $b+c, c+a, a+b$ respectively on the right hand side, the given inequality becomes 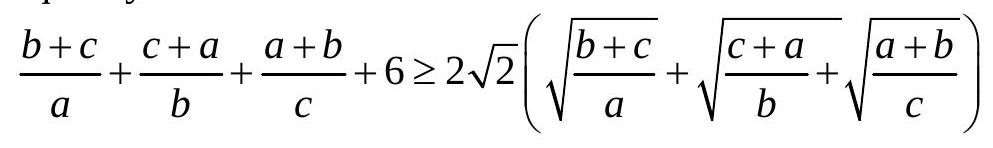![](https://cdn.mathpix.com/cropped/2024_06_05_0ffcf6c39e8d83d98455g-1.jpg?height=148&width=993&top_left_y=1268&top_left_x=497) and equivalently $$ \left(\frac{b+c}{a}-2 \sqrt{2} \sqrt{\frac{b+c}{a}}+2\right)+\left(\frac{c+a}{b}-2 \sqrt{2} \sqrt{\frac{c+a}{b}}+2\right)+\left(\frac{a+b}{c}-2 \sqrt{2} \sqrt{\frac{a+b}{c}}+2\right) \geq 0 $$ which can be written as $$ \left(\sqrt{\frac{b+c}{a}}-\sqrt{2}\right)^{2}+\left(\sqrt{\frac{c+a}{b}}-\sqrt{2}\right)^{2}+\left(\sqrt{\frac{a+b}{c}}-\sqrt{2}\right)^{2} \geq 0 $$ which is true. The equality holds if and only if $$ \frac{b+c}{a}=\frac{c+a}{b}=\frac{a+b}{c} $$ which together with the given condition $a+b+c=1$ gives $a=b=c=\frac{1}{3}$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">=b==\frac{1}{3}</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="10"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Problem 2 Let the circles $k_{1}$ and $k_{2}$ intersect at two distinct points $A$ and $B$, and let $t$ be a common tangent of $k_{1}$ and $k_{2}$, that touches $k_{1}$ and $k_{2}$ at $M$ and $N$, respectively. If $t \perp A M$ and $M N=2 A M$, evaluate $\angle N M B$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution 1 Let $P$ be the symmetric of $A$ with respect to $M$ (Figure 1). Then $A M=M P$ and $t \perp A P$, hence the triangle $A P N$ is isosceles with $A P$ as its base, so $\angle N A P=\angle N P A$. We have $\angle B A P=\angle B A M=\angle B M N$ and $\angle B A N=\angle B N M$. Thus we have $$ 180^{\circ}-\angle N B M=\angle B N M+\angle B M N=\angle B A N+\angle B A P=\angle N A P=\angle N P A $$ so the quadrangle $M B N P$ is cyclic (since the points $B$ and $P$ lie on different sides of $M N$ ). Hence $\angle A P B=\angle M P B=\angle M N B$ and the triangles $A P B$ and $M N B$ are congruent ( $M N=2 A M=A M+M P=A P$ ). From that we get $A B=M B$, i.e. the triangle $A M B$ is isosceles, and since $t$ is tangent to $k_{1}$ and perpendicular to $A M$, the centre of $k_{1}$ is on $A M$, hence $A M B$ is a right-angled triangle. From the last two statements we infer $\angle A M B=45^{\circ}$, and so $\angle N M B=90^{\circ}-\angle A M B=45^{\circ}$. ![](https://cdn.mathpix.com/cropped/2024_06_05_0ffcf6c39e8d83d98455g-2.jpg?height=423&width=809&top_left_y=1162&top_left_x=632) Figure 1 </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">45</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="11"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Problem 3 On a board there are $n$ nails each two connected by a string. Each string is colored in one of $n$ given distinct colors. For each three distinct colors, there exist three nails connected with strings in these three colors. Can $n$ be a) 6 ? b) 7 ? </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. (a) The answer is no. Suppose it is possible. Consider some color, say blue. Each blue string is the side of 4 triangles formed with vertices on the given points. As there exist $\binom{5}{2}=\frac{5 \cdot 4}{2}=10$ pairs of colors other than blue, and for any such pair of colors together with the blue color there exists a triangle with strings in these colors, we conclude that there exist at least 3 blue strings (otherwise the number of triangles with a blue string as a side would be at most $2 \cdot 4=8$, a contradiction). The same is true for any color, so altogether there exist at least $6 \cdot 3=18$ strings, while we have just $\binom{6}{2}=\frac{6 \cdot 5}{2}=15$ of them. (b) The answer is yes Put the nails at the vertices of a regular 7-gon and color each one of its sides in a different color. Now color each diagonal in the color of the unique side parallel to it. It can be checked directly that each triple of colors appears in some triangle (because of symmetry, it is enough to check only the triples containing the first color). ![](https://cdn.mathpix.com/cropped/2024_06_05_0ffcf6c39e8d83d98455g-3.jpg?height=794&width=780&top_left_y=1322&top_left_x=638) Remark. The argument in (a) can be applied to any even n. The argument in (b) can be applied to any odd $n=2 k+1$ as follows: first number the nails as $0,1,2 \ldots, 2 k$ and similarly number the colors as $0,1,2 \ldots, 2 k$. Then connect nail $x$ with nail $y$ by a string of color $x+y(\bmod n)$. For each triple of colors $(p, q, r)$ there are vertices $x, y, z$ connected by these three colors. Indeed, we need to solve $(\bmod n)$ the system $$ (*)(x+y \equiv p, x+z \equiv q, y+z \equiv r) $$ Adding all three, we get $2(x+y+z) \equiv p+q+r$ and multiplying by $k+1$ we get $x+y+z \equiv(k+1)(p+q+r)$. We can now find $x, y, z$ from the identities $(*)$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="12"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Problem 4 Find all positive integers $x, y, z$ and $t$ such that $$ 2^{x} \cdot 3^{y}+5^{z}=7^{t} $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution Reducing modulo 3 we get $5^{z} \equiv 1$, therefore $z$ is even, $z=2 c, c \in \mathbb{N}$. Next we prove that $t$ is even: Obviously, $t \geq 2$. Let us suppose that $t$ is odd, say $t=2 d+1, d \in \mathbb{N}$. The equation becomes $2^{x} \cdot 3^{y}+25^{c}=7 \cdot 49^{d}$. If $x \geq 2$, reducing modulo 4 we get $1 \equiv 3$, a contradiction. And if $x=1$, we have $2 \cdot 3^{y}+25^{c}=7 \cdot 49^{d}$ and reducing modulo 24 we obtain $$ 2 \cdot 3^{y}+1 \equiv 7 \Rightarrow 24 \mid 2\left(3^{y}-3\right) \text {, i.e. } 4 \mid 3^{y-1}-1 $$ which means that $y-1$ is even. Then $y=2 b+1, b \in \mathbb{N}$. We obtain $6 \cdot 9^{b}+25^{c}=7 \cdot 49^{d}$, and reducing modulo 5 we get $(-1)^{b} \equiv 2 \cdot(-1)^{d}$, which is false for all $b, d \in \mathbb{N}$. Hence $t$ is even, $t=2 d, d \in \mathbb{N}$, as claimed. Now the equation can be written as $$ 2^{x} \cdot 3^{y}+25^{d}=49^{d} \Leftrightarrow 2^{x} \cdot 3^{y}=\left(7^{d}-5^{c}\right)\left(7^{d}+5^{c}\right) $$ As $\operatorname{gcd}\left(7^{d}-5^{c}, 7^{d}+5^{c}\right)=2$ and $7^{d}+5^{c}>2$, there exist exactly three possibilities: (1) $\left\{\begin{array}{l}7^{\mathrm{d}}-5^{\mathrm{d}}=2^{\mathrm{x-1}} \\ 7^{\mathrm{d}}+5^{\mathrm{d}}=2 \cdot 3^{y}\end{array} ;\right.$ (2) $\left\{\begin{array}{l}7^{\mathrm{d}}-5^{\mathrm{d}}=2 \cdot 3^{\mathrm{y}} \\ 7^{\mathrm{d}}+5^{\mathrm{d}}=2^{\mathrm{x-1}}\end{array}\right.$; (3) $\left\{\begin{array}{l}7^{d}-5^{d}=2 \\ 7^{d}+5^{d}=2^{x-1} \cdot 3^{y}\end{array}\right.$ ## Case (1) We have $7^{d}=2^{x-2}+3^{y}$ and reducing modulo 3 , we get $2^{x-2} \equiv 1(\bmod 3)$, hence $x-2$ is even, i.e. $x=2 a+2, a \in \mathbb{N}$, where $a>0$, since $a=0$ would mean $3^{y}+1=7^{d}$, which is impossible (even $=$ odd). We obtain $$ 7^{d}-5^{d}=2 \cdot 4^{a} \stackrel{\bmod 4}{\Rightarrow} 7^{d} \equiv 1(\bmod 4) \Rightarrow d=2 e, e \in \mathbb{N} $$ Then we have $$ 49^{e}-5^{d}=2 \cdot 4^{a} \stackrel{\bmod 8}{\Rightarrow} 5^{c} \equiv 1(\bmod 8) \Rightarrow c=2 f, f \in \mathbb{N} $$ We obtain $49^{e}-25^{f}=2 \cdot 4^{a} \stackrel{\text { mod } 3}{\Rightarrow} 0 \equiv 2(\bmod 3)$, false. In conclusion, in this case there are no solutions to the equation. ## Case (2) From $2^{x-1}=7^{d}+5^{c} \geq 12$ we obtain $x \geq 5$. Then $7^{d}+5^{c} \equiv 0(\bmod 4)$, i.e. $3^{d}+1 \equiv 0(\bmod 4)$, hence $d$ is odd. As $7^{d}=5^{c}+2 \cdot 3^{y} \geq 11$, we get $d \geq 2$, hence $d=2 e+1, e \in \mathbb{N}$. As in the previous case, from $7^{d}=2^{x-2}+3^{y}$ reducing modulo 3 we obtain $x=2 a+2$ with $a \geq 2$ (because $x \geq 5$ ). We get $7^{d}=4^{a}+3^{y}$ i.e. $7 \cdot 49^{e}=4^{a}+3^{y}$, hence, reducing modulo 8 we obtain $7 \equiv 3^{y}$ which is false, because $3^{y}$ is congruent either to 1 (if $y$ is even) or to 3 (if $y$ is odd). In conclusion, in this case there are no solutions to the equation. ## Case (3) From $7^{d}=5^{c}+2$ it follows that the last digit of $7^{d}$ is 7 , hence $d=4 k+1, k \in \mathbb{N}$. If $c \geq 2$, from $7^{4 k+1}=5^{c}+2$ reducing modulo 25 we obtain $7 \equiv 2(\bmod 25)$ which is false. For $c=1$ we get $d=1$ and the solution $x=3, y=1, z=t=2$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">3,1,=2</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="13"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 1. The real numbers $a, b, c, d$ satisfy simultaneously the equations $$ a b c-d=1, b c d-a=2, c d a-b=3, d a b-c=-6 $$ Prove that $a+b+c+d \neq 0$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Suppose that $a+b+c+d=0$. Then $$ a b c+b c d+c d a+d a b=0 $$ If $a b c d=0$, then one of numbers, say $d$, must be 0 . In this case $a b c=0$, and so at least two of the numbers $a, b, c, d$ will be equal to 0 , making one of the given equations impossible. Hence $a b c d \neq 0$ and, from (1), $$ \frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}=0 $$ implying $$ \frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c} $$ It follows that $(a+b)(b+c)(c+a)=0$, which is impossible (for instance, if $a+b=0$, then adding the second and third given equations would lead to $0=2+3$, a contradiction). Thus $a+b+c+d \neq 0$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Algebra</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="14"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 3. Let $A L$ and $B K$ be angle bisectors in the non-isosceles triangle $A B C$ ( $L$ lies on the side $B C, K$ lies on the side $A C$ ). The perpendicular bisector of $B K$ intersects the line $A L$ at point $M$. Point $N$ lies on the line $B K$ such that $L N$ is parallel to $M K$. Prove that $L N=N A$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. The point $M$ lies on the circumcircle of $\triangle A B K$ (since both $A L$ and the perpendicular bisector of $B K$ bisect the arc $B K$ of this circle). Then $\angle C B K=$ $\angle A B K=\angle A M K=\angle N L A$. Thus $A B L N$ is cyclic, whence $\angle N A L=\angle N B L=$ $\angle C B K=\angle N L A$. Now it follows that $L N=N A$. ![](https://cdn.mathpix.com/cropped/2024_06_05_3a1fd0d6eb71bd45a2e0g-2.jpg?height=440&width=719&top_left_y=400&top_left_x=677) </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">LN=NA</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="15"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 4. A $9 \times 7$ rectangle is tiled with tiles of the two types shown in the picture below (the tiles are composed by three, respectively four unit squares and the L-shaped tiles can be rotated repeatedly with $90^{\circ}$ ). ![](https://cdn.mathpix.com/cropped/2024_06_05_3a1fd0d6eb71bd45a2e0g-2.jpg?height=130&width=506&top_left_y=1094&top_left_x=776) Let $n \geqslant 0$ be the number of the $2 \times 2$ tiles which can be used in such a tiling. Find all the values of $n$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Answer: 0 or 3 . Denote by $x$ the number of the pieces of the type ornerănd by $y$ the number of the pieces of the type of $2 \times 2$. Mark 20 squares of the rectangle as in the figure below. ![](https://cdn.mathpix.com/cropped/2024_06_05_3a1fd0d6eb71bd45a2e0g-2.jpg?height=300&width=389&top_left_y=1549&top_left_x=842) Obviously, each piece covers at most one marked square. Thus, $x+y \geq 20$ (1) and consequently $3 x+3 y \geq 60(2)$. On the other hand $3 x+4 y=63$ (3). From (2) and (3) it follows $y \leq 3$ and from (3), $3 \mid y$. The proof is finished if we produce tilings with 3 , respectively $0,2 \times 2$ tiles: ![](https://cdn.mathpix.com/cropped/2024_06_05_3a1fd0d6eb71bd45a2e0g-2.jpg?height=306&width=834&top_left_y=2130&top_left_x=614) </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">0or3</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Incomplete</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="16"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 1. Let $n(n \geq 1)$ be an integer. Consider the equation $$ 2 \cdot\left\lfloor\frac{1}{2 x}\right\rfloor-n+1=(n+1)(1-n x) $$ where $x$ is the unknown real variable. (a) Solve the equation for $n=8$. (b) Prove that there exists an integer $n$ for which the equation has at least 2021 solutions. (For any real number $y$ by $\lfloor y\rfloor$ we denote the largest integer $m$ such that $m \leq y$.) </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Let $k=\left[\frac{1}{2 x}\right], k \in \mathbb{Z}$. (a) For $n=8$, the equation becomes $$ k=\left[\frac{1}{2 x}\right]=8-36 x \Rightarrow x \neq 0 \text { and } x=\frac{8-k}{36} $$ Since $x \neq 0$, we have $k \neq 8$, and the last relation implies $k=\left[\frac{1}{2 x}\right]=\left[\frac{18}{8-k}\right]$. Checking signs, we see that $02021$ ensures that there exist at least 2021 integer values of $k$ which satisfy (2). </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"></div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Algebra</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="17"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 2. For any set $A=\left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right\}$ of five distinct positive integers denote by $S_{A}$ the sum of its elements, and denote by $T_{A}$ the number of triples $(i, j, k)$ with $1 \leqslant i<j<k \leqslant 5$ for which $x_{i}+x_{j}+x_{k}$ divides $S_{A}$. Find the largest possible value of $T_{A}$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. We will prove that the maximum value that $T_{A}$ can attain is 4 . Let $A=$ $\left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right\}$ be a set of five positive integers such that $x_{1}x_{4}$ and $x_{3}>x_{2}$. Analogously we can show that any triple of form $(x, y, 5)$ where $y>2$ isn't good. By above, the number of good triples can be at most 5 and only triples $(1,2,5),(2,3,4)$, $(1,3,4),(1,2,4),(1,2,3)$ can be good. But if triples $(1,2,5)$ and $(2,3,4)$ are simultaneously good we have that: $$ x_{1}+x_{2}+x_{5} \mid x_{3}+x_{4} \Rightarrow x_{5}<x_{3}+x_{4} $$ and $$ x_{2}+x_{3}+x_{4} \mid x_{1}+x_{5} \Rightarrow x_{2}+x_{3}+x_{4} \leqslant x_{1}+x_{5} \stackrel{(1)}{<} x_{1}+x_{3}+x_{4}<x_{2}+x_{3}+x_{4}, $$ which is impossible. Therefore, $T_{A} \leqslant 4$. Alternatively, one can prove the statement above by adding up the two inequalities $x_{1}+x_{2}+x_{4}<x_{3}+x_{4}$ and $x_{2}+x_{3}+x_{4}<x_{1}+x_{5}$ that are derived from the divisibilities. To show that $T_{A}=4$ is possible, consider the numbers $1,2,3,4,494$. This works because $6|498,7| 497,8 \mid 496$, and $9 \mid 495$. Remark. The motivation for construction is to realize that if we choose $x_{1}, x_{2}, x_{3}, x_{4}$ we can get all the conditions $x_{5}$ must satisfy. Let $S=x_{1}+x_{2}+x_{3}+x_{4}$. Now we have to choose $x_{5}$ such that $$ S-x_{i} \mid x_{i}+x_{5} \text {, i.e. } x_{5} \equiv-x_{i} \quad \bmod \left(S-x_{i}\right) \forall i \in\{1,2,3,4\} $$ By the Chinese Remainder Theorem it is obvious that if $S-x_{1}, S-x_{2}, S-x_{3}, S-x_{4}$ are pairwise coprime, such $x_{5}$ must exist. To make all these numbers pairwise coprime it's natural to take $x_{1}, x_{2}, x_{3}, x_{4}$ to be all odd and then solve mod 3 issues. Fortunately it can be seen that $1,5,7,11$ easily works because $13,17,19,23$ are pairwise coprime. However, even without the knowledge of this theorem it makes sense intuitively that this system must have a solution for some $x_{1}, x_{2}, x_{3}, x_{4}$. By taking $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=$ $(1,2,3,4)$ we get pretty simple system which can be solved by hand rather easily. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">4</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="18"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 3. Let $A B C$ be an acute scalene triangle with circumcenter $O$. Let $D$ be the foot of the altitude from $A$ to the side $B C$. The lines $B C$ and $A O$ intersect at $E$. Let $s$ be the line through $E$ perpendicular to $A O$. The line $s$ intersects $A B$ and $A C$ at $K$ and $L$, respectively. Denote by $\omega$ the circumcircle of triangle $A K L$. Line $A D$ intersects $\omega$ again at $X$. Prove that $\omega$ and the circumcircles of triangles $A B C$ and $D E X$ have a common point. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution. ![](https://cdn.mathpix.com/cropped/2024_06_05_59a54a44649abed37d52g-3.jpg?height=821&width=853&top_left_y=798&top_left_x=598) Let us denote angles of triangle $A B C$ with $\alpha, \beta, \gamma$ in a standard way. By basic anglechasing we have $$ \angle B A D=90^{\circ}-\beta=\angle O A C \text { and } \angle C A D=\angle B A O=90^{\circ}-\gamma $$ Using the fact that lines $A E$ and $A X$ are isogonal with respect to $\angle K A L$ we can conclude that $X$ is an $A$-antipode on $\omega$. (This fact can be purely angle-chased: we have $$ \angle K A X+\angle A X K=\angle K A X+\angle A L K=90^{\circ}-\beta+\beta=90^{\circ} $$ which implies $\angle A K X=90^{\circ}$ ). Now let $F$ be the projection of $X$ on the line $A E$. Using that $A X$ is a diameter of $\omega$ and $\angle E D X=90^{\circ}$ it's clear that $F$ is the intersection point of $\omega$ and the circumcircle of triangle $D E X$. Now it suffices to show that $A B F C$ is cyclic. We have $\angle K L F=\angle K A F=90^{\circ}-\gamma$ and from $\angle F E L=90^{\circ}$ we have that $\angle E F L=\gamma=\angle E C L$ so quadrilateral $E F C L$ is cyclic. Next, we have $$ \angle A F C=\angle E F C=180^{\circ}-\angle E L C=\angle E L A=\beta $$ (where last equality holds because of $\angle A E L=90^{\circ}$ and $\angle E A L=90^{\circ}-\beta$ ). ![](https://cdn.mathpix.com/cropped/2024_06_05_59a54a44649abed37d52g-4.jpg?height=834&width=857&top_left_y=369&top_left_x=596) </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="19"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 4. Let $M$ be a subset of the set of 2021 integers $\{1,2,3, \ldots, 2021\}$ such that for any three elements (not necessarily distinct) $a, b, c$ of $M$ we have $|a+b-c|>10$. Determine the largest possible number of elements of $M$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. The set $M=\{1016,1017, \ldots, 2021\}$ has 1006 elements and satisfies the required property, since $a, b, c \in M$ implies that $a+b-c \geqslant 1016+1016-2021=11$. We will show that this is optimal. Suppose $M$ satisfies the condition in the problem. Let $k$ be the minimal element of $M$. Then $k=|k+k-k|>10 \Rightarrow k \geqslant 11$. Note also that for every $m$, the integers $m, m+k-10$ cannot both belong to $M$, since $k+m-(m+k-10)=10$. Claim 1: $M$ contains at most $k-10$ out of any $2 k-20$ consecutive integers. Proof: We can partition the set $\{m, m+1, \ldots, m+2 k-21\}$ into $k-10$ pairs as follows: $$ \{m, m+k-10\},\{m+1, m+k-9\}, \ldots,\{m+k-11, m+2 k-21\} $$ It remains to note that $M$ can contain at most one element of each pair. Claim 2: $M$ contains at most $[(t+k-10) / 2]$ out of any $t$ consecutive integers. Proof: Write $t=q(2 k-20)+r$ with $r \in\{0,1,2 \ldots, 2 k-21\}$. From the set of the first $q(2 k-20)$ integers, by Claim 1 at most $q(k-10)$ can belong to $M$. Also by claim 1, it follows that from the last $r$ integers, at $\operatorname{most} \min \{r, k-10\}$ can belong to $M$. Thus, - If $r \leqslant k-10$, then at most $$ q(k-10)+r=\frac{t+r}{2} \leqslant \frac{t+k-10}{2} \text { integers belong to } M $$ - If $r>k-10$, then at most $$ q(k-10)+k-10=\frac{t-r+2(k-10)}{2} \leqslant \frac{t+k-10}{2} \text { integers belong to } M $$ By Claim 2, the number of elements of $M$ amongst $k+1, k+2, \ldots, 2021$ is at most $$ \left[\frac{(2021-k)+(k-10)}{2}\right]=1005 $$ Since amongst $\{1,2, \ldots, k\}$ only $k$ belongs to $M$, we conclude that $M$ has at most 1006 elements as claimed. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">1006</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="20"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 1. Find all distinct prime numbers $p, q$ and $r$ such that $$ 3 p^{4}-5 q^{4}-4 r^{2}=26 $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. First notice that if both primes $q$ and $r$ differ from 3 , then $q^{2} \equiv r^{2} \equiv 1(\bmod 3)$, hence the left hand side of the given equation is congruent to zero modulo 3 , which is impossible since 26 is not divisible by 3 . Thus, $q=3$ or $r=3$. We consider two cases. Case 1. $q=3$. The equation reduces to $3 p^{4}-4 r^{2}=431$ If $p \neq 5, \quad$ by Fermat's little theorem, $\quad p^{4} \equiv 1(\bmod 5)$, which yields $3-4 r^{2} \equiv 1(\bmod 5), \quad$ or equivalently, $\quad r^{2}+2 \equiv 0(\bmod 5)$. The last congruence is impossible in view of the fact that a residue of a square of a positive integer belongs to the set $\{0,1,4\}$. Therefore $p=5$ and $r=19$. Case 2. $r=3$. The equation becomes $3 p^{4}-5 q^{4}=62$ Obviously $p \neq 5$. Hence, Fermat's little theorem gives $p^{4} \equiv 1(\bmod 5)$. But then $5 q^{4} \equiv 1(\bmod 5)$, which is impossible . Hence, the only solution of the given equation is $p=5, q=3, r=19$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">p=5,q=3,r=19</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="21"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 2. Consider an acute triangle $A B C$ with area S. Let $C D \perp A B \quad(D \in A B)$, $D M \perp A C \quad(M \in A C)$ and $\quad D N \perp B C \quad(N \in B C)$. Denote by $H_{1}$ and $H_{2}$ the orthocentres of the triangles $M N C$ and $M N D$ respectively. Find the area of the quadrilateral $\mathrm{AH}_{1} \mathrm{BH}_{2}$ in terms of $S$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution 1. Let $O, P, K, R$ and $T$ be the mid-points of the segments $C D, M N$, $C N, C H_{1}$ and $M H_{1}$, respectively. From $\triangle M N C$ we have that $\overline{P K}=\frac{1}{2} \overline{M C}$ and $P K \| M C$. Analogously, from $\Delta M H_{1} C$ we have that $\overline{T R}=\frac{1}{2} \overline{M C}$ and $T R \| M C$. Consequently, $\overline{P K}=\overline{T R}$ and $P K \| T R$. Also $O K \| D N \quad$ (from ![](https://cdn.mathpix.com/cropped/2024_06_05_e8f9a14accde81c04529g-2.jpg?height=657&width=834&top_left_y=554&top_left_x=994) $\triangle C D N$ ) and since $D N \perp B C$ and $M H_{1} \perp B C$, it follows that $T H_{1} \| O K$. Since $O$ is the circumcenter of $\triangle C M N, O P \perp M N$. Thus, $C H_{1} \perp M N$ implies $O P \| C H_{1}$. We conclude $\triangle T R H_{1} \cong \triangle K P O \quad$ (they have parallel sides and $\overline{T R}=\overline{P K}$ ), hence $\overline{R H_{1}}=\overline{P O}$, i.e. $\overline{C H_{1}}=2 \overline{P O}$ and $C H_{1} \| P O$. Analogously, $\overline{D H_{2}}=2 \overline{P O} \quad$ and $\quad D H_{2} \| P O$. From $\quad \overline{C H_{1}}=2 \overline{P O}=\overline{D H_{2}} \quad$ and $C H_{1}\|P O\| D H_{2}$ the quadrilateral $C H_{1} H_{2} D$ is a parallelogram, thus $\overline{H_{1} H_{2}}=\overline{C D}$ and $H_{1} H_{2} \| C D$. Therefore the area of the quadrilateral $A H_{1} B H_{2}$ is $\frac{\overline{A B} \cdot \overline{H_{1} H_{2}}}{2}=\frac{\overline{A B} \cdot \overline{C D}}{2}=S$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">S</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="22"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 3. Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that $$ \left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq 3(a+b+c+1) $$ When does equality hold? </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution 1. By using AM-GM $\left(x^{2}+y^{2}+z^{2} \geq x y+y z+z x\right)$ we have $$ \begin{aligned} \left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} & \geq\left(a+\frac{1}{b}\right)\left(b+\frac{1}{c}\right)+\left(b+\frac{1}{c}\right)\left(c+\frac{1}{a}\right)+\left(c+\frac{1}{a}\right)\left(a+\frac{1}{b}\right) \\ & =\left(a b+1+\frac{a}{c}+a\right)+\left(b c+1+\frac{b}{a}+b\right)+\left(c a+1+\frac{c}{b}+c\right) \\ & =a b+b c+c a+\frac{a}{c}+\frac{c}{b}+\frac{b}{a}+3+a+b+c \end{aligned} $$ Notice that by AM-GM we have $a b+\frac{b}{a} \geq 2 b, b c+\frac{c}{b} \geq 2 c$, and $c a+\frac{a}{c} \geq 2 a$. Thus , $\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq\left(a b+\frac{b}{a}\right)+\left(b c+\frac{c}{b}\right)+\left(c a+\frac{a}{c}\right)+3+a+b+c \geq 3(a+b+c+1)$. The equality holds if and only if $a=b=c=1$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="23"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 4. For a positive integer $n$, two players A and B play the following game: Given a pile of $s$ stones, the players take turn alternatively with A going first. On each turn the player is allowed to take either one stone, or a prime number of stones, or a multiple of $n$ stones. The winner is the one who takes the last stone. Assuming both $\mathrm{A}$ and $\mathrm{B}$ play perfectly, for how many values of $s$ the player A cannot win? </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Denote by $k$ the sought number and let $\left\{s_{1}, \mathrm{~s}_{2}, \ldots, \mathrm{s}_{k}\right\}$ be the corresponding values for $s$. We call each $s_{i}$ a losing number and every other nonnegative integer a winning numbers. ## Clearly every multiple of $n$ is a winning number. Suppose there are two different losing numbers $s_{i}>s_{j}$, which are congruent modulo $n$. Then, on his first turn of play, player $A$ may remove $s_{i}-s_{j}$ stones (since $n \mid s_{i}-s_{j}$ ), leaving a pile with $s_{j}$ stones for B. This is in contradiction with both $s_{i}$ and $s_{j}$ being losing numbers. Hence, there are at most $n-1$ losing numbers, i.e. $k \leq n-1$. Suppose there exists an integer $r \in\{1,2, \ldots, n-1\}$, such that $m n+r$ is a winning number for every $m \in \mathbb{N}_{0}$. Let us denote by $u$ the greatest losing number (if $k>0$ ) or 0 (if $k=0)$, and let $s=\operatorname{LCM}(2,3, \ldots, u+n+1)$. Note that all the numbers $s+2, s+3, \ldots$, $s+u+n+1 \quad$ are composite. Let $m^{\prime} \in \mathbb{N}_{0}$, be such that $s+u+2 \leq m^{\prime} n+r \leq s+u+n+1$. In order for $m^{\prime} n+r$ to be a winning number, there must exist an integer $p$, which is either one, or prime, or a positive multiple of $n$, such that $m^{\prime} n+r-p$ is a losing number or 0 , and hence lesser than or equal to $u$. Since $s+2 \leq m^{\prime} n+r-u \leq p \leq m^{\prime} n+r \leq s+u+n+1, p$ must be a composite, hence $p$ is a multiple of $n$ (say $p=q n$ ). But then $m^{\prime} n+r-p=\left(m^{\prime}-q\right) n+r$ must be a winning number, according to our assumption. This contradicts our assumption that all numbers $m n+r, m \in \mathbb{N}_{0}$ are winning. Hence, each nonzero residue class modulo $n$ contains a loosing number. There are exactly $n-1$ losing numbers . Lemma: No pair $(u, n)$ of positive integers satisfies the following property: $(*) \quad$ In $\mathbb{N}$ exists an arithmetic progression $\left(a_{t}\right)_{t=1}^{\infty}$ with difference $n$ such that each segment $\left[a_{i}-u, a_{i}+u\right]$ contains a prime. Proof of the lemma: Suppose such a pair $(u, n)$ and a corresponding arithmetic progression $\left(\mathrm{a}_{t}\right)_{t=1}^{\infty}$ exist. In $\mathbb{N}$ exist arbitrarily long patches of consecutive composites. Take such a patch $P$ of length $3 u n$. Then, at least one segment $\left[a_{i}-u, a_{i}+u\right]$ is fully contained in $P$, a contradiction. Suppose such a nonzero residue class modulo $n$ exists (hence $n>1$ ). Let $u \in \mathbb{N}$ be greater than every loosing number. Consider the members of the supposed residue class which are greater than $u$. They form an arithmetic progression with the property $\left({ }^{*}\right)$, a contradiction (by the lemma). </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">n-1</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="24"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 1. Find all pairs $(a, b)$ of positive integers such that $$ 11 a b \leq a^{3}-b^{3} \leq 12 a b $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution 1. Let $a-b=t$. Due to $a^{3}-b^{3} \geq 11 a b$ we conclude that $a>b$ so $t$ is a positive integer and the condition can be written as $$ 11 b(b+t) \leq t\left[b^{2}+b(b+t)+(b+t)^{2}\right] \leq 12 b(b+t) $$ Since $$ t\left[b^{2}+b(b+t)+(b+t)^{2}\right]=t\left(b^{2}+b^{2}+b t+b^{2}+2 b t+t^{2}\right)=3 t b(b+t)+t^{3} $$ the condition can be rewritten as $$ (11-3 t) b(b+t) \leq t^{3} \leq(12-3 t) b(b+t) $$ We can not have $t \geq 4$ since in that case $t^{3} \leq(12-3 t) b(b+t)$ is not satisfied as the right hand side is not positive. Therefore it remains to check the cases when $t \in\{1,2,3\}$. If $t=3$, the above condition becomes $$ 2 b(b+3) \leq 27 \leq 3 b(b+3) $$ If $b \geq 3$, the left hand side is greater than 27 and if $b=1$ the right hand side is smaller than 27 so there are no solutions in these cases. If $b=2$, we get a solution $(a, b)=(5,2)$. If $t \leq 2$, we have $$ (11-3 t) b(b+t) \geq(11-6) \cdot 1 \cdot(1+1)=10>t^{3} $$ so there are no solutions in this case. In summary, the only solution is $(a, b)=(5,2)$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">(5,2)</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="25"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 2. Let $A B C$ be an acute triangle such that $A H=H D$, where $H$ is the orthocenter of $A B C$ and $D \in B C$ is the foot of the altitude from the vertex $A$. Let $\ell$ denote the line through $H$ which is tangent to the circumcircle of the triangle $B H C$. Let $S$ and $T$ be the intersection points of $\ell$ with $A B$ and $A C$, respectively. Denote the midpoints of $B H$ and $C H$ by $M$ and $N$, respectively. Prove that the lines $S M$ and $T N$ are parallel. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution 1. In order to prove that $S M$ and $T N$ are parallel, it suffices to prove that both of them are perpendicular to $S T$. Due to symmetry, we will provide a detailed proof of $S M \perp S T$, whereas the proof of $T N \perp S T$ is analogous. In this solution we will use the following notation: $\angle B A C=\alpha, \angle A B C=\beta, \angle A C B=\gamma$. ![](https://cdn.mathpix.com/cropped/2024_06_05_6dbeb2bed8a94e31d91eg-3.jpg?height=1047&width=1489&top_left_y=913&top_left_x=318) We first observe that, due to the tangency condition, we have $$ \angle S H B=\angle H C B=90^{\circ}-\beta $$ Combining the above with $$ \angle S B H=\angle A B H=90^{\circ}-\alpha $$ we get $$ \angle B S H=180^{\circ}-\left(90^{\circ}-\beta\right)-\left(90^{\circ}-\alpha\right)=\alpha+\beta=180^{\circ}-\gamma $$ from which it follows that $\angle A S T=\gamma$. Since $A H=H D, H$ is the midpoint of $A D$. If $K$ denotes the midpoint of $A B$, we have that $K H$ and $B C$ are parallel. Since $M$ is the midpoint of $B H$, the lines $K M$ and $A D$ are parallel, from which it follows that $K M$ is perpendicular to $B C$. As $K H$ and $B C$ are parallel, we have that $K M$ is perpendicular to $K H$ so $\angle M K H=90^{\circ}$. Using the parallel lines $K H$ and $B C$ we also have $$ \angle K H M=\angle K H B=\angle H B C $$ Now, $$ \angle H M K=90^{\circ}-\angle K H M=90^{\circ}-\angle H B C=90^{\circ}-\left(90^{\circ}-\gamma\right)=\gamma=\angle A S T=\angle K S H $$ so the quadrilateral $M S K H$ is cyclic, which implies that $\angle M S H=\angle M K H=90^{\circ}$. In other words, the lines $S M$ and $S T$ are perpendicular, which completes our proof. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="26"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 4. We call an even positive integer $n$ nice if the set $\{1,2, \ldots, n\}$ can be partitioned into $\frac{n}{2}$ two-element subsets, such that the sum of the elements in each subset is a power of 3 . For example, 6 is nice, because the set $\{1,2,3,4,5,6\}$ can be partitioned into subsets $\{1,2\},\{3,6\},\{4,5\}$. Find the number of nice positive integers which are smaller than $3^{2022}$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. For a nice number $n$ and a given partition of the set $\{1,2, \ldots, n\}$ into twoelement subsets such that the sum of the elements in each subset is a power of 3 , we say that $a, b \in\{1,2, \ldots, n\}$ are paired if both of them belong to the same subset. Let $x$ be a nice number and $k$ be a (unique) non-negative integer such that $3^{k} \leq x3^{k} $$ implies that $s>k$. From these we conclude that $s$ must be equal to $k+1$, so $x+y=3^{k+1}$. The last equation, combined with $x>y$, implies that $x>\frac{3^{k+1}}{2}$. Similarly as above, we can conclude that each number $z$ from the closed interval $\left[3^{k+1}-x, x\right]$ is paired with $3^{k+1}-z$. Namely, for any such $z$, the larger of the numbers $z$ and $3^{k+1}-z$ is greater than $\frac{3^{k+1}}{2}$ which is greater than $3^{k}$, so the numbers $z$ and $3^{k+1}-z$ must necessarily be in the same subset. In other words, each number from the interval $\left[3^{k+1}-x, x\right]$ is paired with another number from this interval. Note that this implies that all numbers smaller than $3^{k+1}-x$ are paired among themselves, so the number $3^{k+1}-x-1$ is either nice or equals zero. Also, the number $3^{k}$ must be paired with $2 \cdot 3^{k}$, so $x \geq 2 \cdot 3^{k}$. Finally, we prove by induction that $a_{n}=2^{n}-1$, where $a_{n}$ is the number of nice positive integers smaller than $3^{n}$. For $n=1$, the claim is obviously true, because 2 is the only nice positive integer smaller than 3 . Now, assume that $a_{n}=2^{n}-1$ for some positive integer $n$. We will prove that $a_{n+1}=2^{n+1}-1$. To prove this, first observe that the number of nice positive integers between $2 \cdot 3^{n}$ and $3^{n+1}$ is exactly $a_{n+1}-a_{n}$. Next, observe that $3^{n+1}-1$ is nice. For every nice number $2 \cdot 3^{n} \leq x<3^{n+1}-1$, the number $3^{n+1}-x-1$ is also nice and is strictly smaller than $3^{n}$. Also, for every positive integer $y<3^{n}$, obviously there is a unique number $x$ such that $2 \cdot 3^{n} \leq x<3^{n+1}-1$ and $3^{n+1}-x-1=y$. Thus, $$ a_{n+1}-a_{n}=a_{n}+1 \Leftrightarrow a_{n+1}=2 a_{n}+1=2\left(2^{n}-1\right)+1=2^{n+1}-1 $$ completing the proof. In summary, there are $2^{2022}-1$ nice positive integers smaller than $3^{2022}$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">2^{2022}-1</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="27"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Problem 1. Find all pairs $(a, b)$ of positive integers such that $a!+b$ and $b!+a$ are both powers of 5 . </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. The condition is symmetric so we can assume that $b \leq a$. The first case is when $a=b$. In this case, $a!+a=5^{m}$ for some positive integer $m$. We can rewrite this as $a \cdot((a-1)!+1)=5^{m}$. This means that $a=5^{k}$ for some integer $k \geq 0$. It is clear that $k$ cannot be 0 . If $k \geq 2$, then $(a-1)!+1=5^{l}$ for some $l \geq 1$, but $a-1=5^{k}-1>5$, so $5 \mid(a-1)$ !, which is not possible because $5 \mid(a-1)!+1$. This means that $k=1$ and $a=5$. In this case, $5!+5=125$, which gives us the solution $(5,5)$. Let us now assume that $1 \leq b5$, so $5 \mid a$ !. However, $5 \mid 5^{y}=a!+1$, which leads to a contradiction. We conclude that $x=1$ and $a=4$. From here $a!+b=25$ and $b!+a=5$, so we get two more solutions: $(1,4)$ and $(4,1)$. Now we focus on the case $1b$. Because $b \mid 5^{x}$ and $b>1$, we have $b=5^{z}$ for $z \geq 1$. If $z \geq 2$, then $5b=5$, which gives us $a \geq 10$. However, this would mean that $25|a!, 5| b$ and $25 \nmid b$, which is not possible, because $a!+b=5^{x}$ and $25 \mid 5^{x}$. We conclude that the only solutions are $(1,4),(4,1)$ and $(5,5)$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">(1,4),(4,1),(5,5)</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="28"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Problem 2. Prove that for all non-negative real numbers $x, y, z$, not all equal to 0 , the following inequality holds $$ \frac{2 x^{2}-x+y+z}{x+y^{2}+z^{2}}+\frac{2 y^{2}+x-y+z}{x^{2}+y+z^{2}}+\frac{2 z^{2}+x+y-z}{x^{2}+y^{2}+z} \geqslant 3 $$ Determine all the triples $(x, y, z)$ for which the equality holds. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Let us first write the expression $L$ on the left hand side in the following way $$ \begin{aligned} L & =\left(\frac{2 x^{2}-x+y+z}{x+y^{2}+z^{2}}+2\right)+\left(\frac{2 y^{2}+x-y+z}{x^{2}+y+z^{2}}+2\right)+\left(\frac{2 z^{2}+x+y-z}{x^{2}+y^{2}+z}+2\right)-6 \\ & =\left(2 x^{2}+2 y^{2}+2 z^{2}+x+y+z\right)\left(\frac{1}{x+y^{2}+z^{2}}+\frac{1}{x^{2}+y+z^{2}}+\frac{1}{x^{2}+y^{2}+z}\right)-6 \end{aligned} $$ If we introduce the notation $A=x+y^{2}+z^{2}, B=x^{2}+y+z^{2}, C=x^{2}+y^{2}+z$, then the previous relation becomes $$ L=(A+B+C)\left(\frac{1}{A}+\frac{1}{B}+\frac{1}{C}\right)-6 $$ Using the arithmetic-harmonic mean inequality or Cauchy-Schwartz inequality for positive real numbers $A, B, C$, we easily obtain $$ (A+B+C)\left(\frac{1}{A}+\frac{1}{B}+\frac{1}{C}\right) \geqslant 9 $$ so it holds $L \geqslant 3$. The equality occurs if and only if $A=B=C$, which is equivalent to the system of equations $$ x^{2}-y^{2}=x-y, \quad y^{2}-z^{2}=y-z, \quad x^{2}-z^{2}=x-z $$ It follows easily that the only solutions of this system are $(x, y, z) \in\{(t, t, t) \mid t>0\} \cup\{(t, t, 1-t) \mid t \in[0,1]\} \cup\{(t, 1-t, t) \mid t \in[0,1]\} \cup\{(1-t, t, t) \mid t \in[0,1]\}$. PSC Remark We feel the equality case needs more explanations in order to have a complete solution, our suggestion follows: Clearly if $x, y, z$ are all equal and not 0 satisfy the condition. Now suppose that not all of them are equal it means we can't simultaneously have $x+y=y+z=z+x=1$ otherwise we would have all $x, y, z$ equal to $\frac{1}{2}$ which we already discussed. We can suppose now that $x=y$ and $y+z=z+x=1$ where we get $z=1-x$. So, all triples which satisfy the equality are $(x, y, z)=(a, a, a),(b, b, 1-b)$ and all permutations for any $a>0$ and $b \in[0,1]$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="29"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Problem 3. Alice and Bob play the following game on a $100 \times 100$ grid, taking turns, with Alice starting first. Initially the grid is empty. At their turn, they choose an integer from 1 to $100^{2}$ that is not written yet in any of the cells and choose an empty cell, and place it in the chosen cell. When there is no empty cell left, Alice computes the sum of the numbers in each row, and her score is the maximum of these 100 sums. Bob computes the sum of the numbers in each column, and his score is the maximum of these 100 sums. Alice wins if her score is greater than Bob's score, Bob wins if his score is greater than Alice's score, otherwise no one wins. Find if one of the players has a winning strategy, and if so which player has a winning strategy. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. We denote by $(i, j)$ the cell in the $i$-th line and in the $j$-th column for every $1 \leq i, j \leq n$. Bob associates the following pair of cells : $(i, 2 k+1),(i, 2 k+2)$ for $1 \leq i \leq 100$ and $0 \leq k \leq 49$ except for $(i, k)=(100,0)$ and $(100,1)$, and the pairs $(100,1),(100,3)$ and $(100,2),(100,4)$. Each time Alice writes the number $j$ in one of the cell, Bob writes the number $100^{2}+1-j$ in the other cell of the pair. One can prove by induction that after each of Bob's turn, for each pair of cell, either there is a number written in each of the cell of the pair, or in neither of them. And that if a number $j$ is written, $100^{2}+1-j$ is also written. Thus Bob can always apply the previous strategy (since $j=100^{2}+1-j$ is impossible). At the end, every line has sum $\left(100^{2}+1\right) \times 50$. Assume by contradiction that Alice can stop Bob from winning if he applies this strategy. Let $c_{j}$ be the sum of the number in the $j$-th column for $1 \leq j \leq 100$ : then $c_{j} \leq 50\left(100^{2}+1\right)$. Note that : $$ 100 \times 50\left(100^{2}+1\right) \geq c_{1}+\cdots+c_{100}=1+\cdots+100^{2}=\frac{100^{2}\left(100^{2}+1\right)}{2}=100 \times 50\left(100^{2}+1\right) $$ Thus we have equality in the previous inequality : $c_{1}=\cdots=c_{100}=50\left(100^{2}+1\right)$. But if $a$ is the number written in the case $(100,1)$ and $b$ the number written in the case $(100,2)$, then $c_{1}-b+c_{2}-c=99\left(100^{2}+1\right)$. Thus $b+c=100\left(100^{2}+1\right)-99\left(100^{2}+1\right)=100^{2}+1$ : by hypothesis $c$ is also written in the cell $(100,3)$ which is a contradiction. Thus Bob has a winning strategy </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="30"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Problem 4. Let $A B C$ be an acute triangle with circumcenter $O$. Let $D$ be the foot of the altitude from $A$ to $B C$ and let $M$ be the midpoint of $O D$. The points $O_{b}$ and $O_{c}$ are the circumcenters of triangles $A O C$ and $A O B$, respectively. If $A O=A D$, prove that the points $A, O_{b}, M$ and $O_{c}$ are concyclic. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution. ![](https://cdn.mathpix.com/cropped/2024_06_05_5f128255869e7ca2fe94g-4.jpg?height=1211&width=920&top_left_y=591&top_left_x=568) Note that $A B=A C$ cannot hold since $A O=A D$ would imply that $O$ is the midpoint of $B C$, which is not possible for an acute triangle. So we may assume without loss of generality that $A B90^{\circ}$ so that $O_{c}$ is in the interior of triangle $A O B$ and $O_{b}$ in external to the triangles $A O C$ (the other cases are analogous and if $\angle A O B=90^{\circ}$ or $\angle A O C=90^{\circ}$, then $M_{b} \equiv O_{b}$ or $M_{c} \equiv O_{c}$ and we are automatically done). We have $$ \angle M_{c} M_{b} O_{b}=90^{\circ}+\angle A M_{b} M_{c}=90^{\circ}+\angle A C B $$ as well as (since $O_{c} O_{b}$ is a perpendicular bisector of $A O$ and hence bisects $\angle A O_{C} O$ ) $$ \angle M_{c} O_{c} O_{b}=180^{\circ}-\angle O O_{c} O_{b}=90^{\circ}+\frac{\angle A O_{c} M_{c}}{2} $$ $$ =90^{\circ}+\frac{\angle A O_{c} B}{4}=90^{\circ}+\frac{\angle A O B}{2}=90^{\circ}+\angle A C B $$ and therefore $O_{b} M_{b} O_{c} M_{c}$ is cyclic, as desired. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Incomplete</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="31"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 1. Find all triples $(a, b, c)$ of real numbers such that the following system holds: $$ \left\{\begin{array}{l} a+b+c=\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \\ a^{2}+b^{2}+c^{2}=\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}} \end{array}\right. $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. First of all if $(a, b, c)$ is a solution of the system then also $(-a,-b,-c)$ is a solution. Hence we can suppose that $a b c>0$. From the first condition we have $$ a+b+c=\frac{a b+b c+c a}{a b c} $$ Now, from the first condition and the second condition we get $$ (a+b+c)^{2}-\left(a^{2}+b^{2}+c^{2}\right)=\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^{2}-\left(\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}\right) $$ The last one simplifies to $$ a b+b c+c a=\frac{a+b+c}{a b c} $$ First we show that $a+b+c$ and $a b+b c+c a$ are different from 0 . Suppose on contrary then from relation (1) or (2) we have $a+b+c=a b+b c+c a=0$. But then we would have $$ a^{2}+b^{2}+c^{2}=(a+b+c)^{2}-2(a b+b c+c a)=0 $$ which means that $a=b=c=0$. This is not possible since $a, b, c$ should be different from 0 . Now multiplying (1) and (2) we have $$ (a+b+c)(a b+b c+c a)=\frac{(a+b+c)(a b+b c+c a)}{(a b c)^{2}} $$ Since $a+b+c$ and $a b+b c+c a$ are different from 0 , we get $(a b c)^{2}=1$ and using the fact that $a b c>0$ we obtain that $a b c=1$. So relations (1) and (2) transform to $$ a+b+c=a b+b c+c a . $$ Therefore, $$ (a-1)(b-1)(c-1)=a b c-a b-b c-c a+a+b+c-1=0 \text {. } $$ This means that at least one of the numbers $a, b, c$ is equal to 1 . Suppose that $c=1$ then relations (1) and (2) transform to $a+b+1=a b+a+b \Rightarrow a b=1$. Taking $a=t$ then we have $b=\frac{1}{t}$. We can now verify that any triple $(a, b, c)=\left(t, \frac{1}{t}, 1\right)$ satisfies both conditions. $t \in \mathbb{R} \backslash\{0\}$. From the initial observation any triple $(a, b, c)=\left(t, \frac{1}{t},-1\right)$ satisfies both conditions. $t \in \mathbb{R} \backslash\{0\}$. So, all triples that satisfy both conditions are $(a, b, c)=\left(t, \frac{1}{t}, 1\right),\left(t, \frac{1}{t},-1\right)$ and all permutations for any $t \in \mathbb{R} \backslash\{0\}$. Comment by PSC. After finding that $a b c=1$ and $$ a+b+c=a b+b c+c a $$ we can avoid the trick considering $(a-1)(b-1)(c-1)$ as follows. By the Vieta's relations we have that $a, b, c$ are roots of the polynomial $$ P(x)=x^{3}-s x^{2}+s x-1 $$ which has one root equal to 1 . Then, we can conclude as in the above solution. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">(,b,)=(,\frac{1}{},1),(,\frac{1}{},-1)</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Algebra</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="32"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 2. Let $\triangle A B C$ be a right-angled triangle with $\angle B A C=90^{\circ}$ and let $E$ be the foot of the perpendicular from $A$ on $B C$. Let $Z \neq A$ be a point on the line $A B$ with $A B=B Z$. Let (c) be the circumcircle of the triangle $\triangle A E Z$. Let $D$ be the second point of intersection of $(c)$ with $Z C$ and let $F$ be the antidiametric point of $D$ with respect to (c). Let $P$ be the point of intersection of the lines $F E$ and $C Z$. If the tangent to (c) at $Z$ meets $P A$ at $T$, prove that the points $T, E, B, Z$ are concyclic. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. We will first show that $P A$ is tangent to $(c)$ at $A$. Since $E, D, Z, A$ are concyclic, then $\angle E D C=\angle E A Z=\angle E A B$. Since also the triangles $\triangle A B C$ and $\triangle E B A$ are similar, then $\angle E A B=\angle B C A$, therefore $\angle E D C=\angle B C A$. Since $\angle F E D=90^{\circ}$, then $\angle P E D=90^{\circ}$ and so $$ \angle E P D=90^{\circ}-\angle E D C=90^{\circ}-\angle B C A=\angle E A C $$ Therefore the points $E, A, C, P$ are concyclic. It follows that $\angle C P A=90^{\circ}$ and therefore the triangle $\angle P A Z$ is right-angled. Since also $B$ is the midpoint of $A Z$, then $P B=A B=B Z$ and so $\angle Z P B=$ $\angle P Z B$. ![](https://cdn.mathpix.com/cropped/2024_06_05_aa04e63f5bdef252b2edg-2.jpg?height=1215&width=1016&top_left_y=1008&top_left_x=530) Furthermore, $\angle E P D=\angle E A C=\angle C B A=\angle E B A$ from which it follows that the points $P, E, B, Z$ are also concyclic. Now observe that $$ \angle P A E=\angle P C E=\angle Z P B-\angle P B E=\angle P Z B-\angle P Z E=\angle E Z B $$ Therefore $P A$ is tangent to $(c)$ at $A$ as claimed. It now follows that $T A=T Z$. Therefore $$ \begin{aligned} \angle P T Z & =180^{\circ}-2(\angle T A B)=180^{\circ}-2(\angle P A E+\angle E A B)=180^{\circ}-2(\angle E C P+\angle A C B) \\ & =180^{\circ}-2\left(90^{\circ}-\angle P Z B\right)=2(\angle P Z B)=\angle P Z B+\angle B P Z=\angle P B A . \end{aligned} $$ Thus $T, P, B, Z$ are concyclic, and since $P, E, B, Z$ are also concyclic then $T, E, B, Z$ are concyclic as required. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="33"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 3. Alice and Bob play the following game: Alice picks a set $A=\{1,2, \ldots, n\}$ for some natural number $n \geqslant 2$. Then starting with Bob, they alternatively choose one number from the set $A$, according to the following conditions: initially Bob chooses any number he wants, afterwards the number chosen at each step should be distinct from all the already chosen numbers, and should differ by 1 from an already chosen number. The game ends when all numbers from the set $A$ are chosen. Alice wins if the sum of all of the numbers that she has chosen is composite. Otherwise Bob wins. Decide which player has a winning strategy. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. To say that Alice has a winning strategy means that she can find a number $n$ to form the set A, so that she can respond appropriately to all choices of Bob and always get at the end a composite number for the sum of her choices. If such $n$ does not exist, this would mean that Bob has a winning strategy instead. Alice can try first to check the small values of $n$. Indeed, this gives the following winning strategy for her: she initially picks $n=8$ and responds to all possible choices made by Bob as in the list below (in each row the choices of Bob and Alice are given alternatively, starting with Bob): $\begin{array}{llllllll}1 & 2 & 3 & 4 & 5 & 6 & 7 & 8\end{array}$ $\begin{array}{llllllll}2 & 3 & 1 & 4 & 5 & 6 & 7 & 8\end{array}$ $\begin{array}{llllllll}2 & 3 & 4 & 1 & 5 & 6 & 7 & 8\end{array}$ $\begin{array}{llllllll}3 & 2 & 1 & 4 & 5 & 6 & 7 & 8\end{array}$ $\begin{array}{llllllll}3 & 2 & 4 & 5 & 1 & 6 & 7 & 8\end{array}$ $\begin{array}{llllllll}3 & 2 & 4 & 5 & 6 & 1 & 7 & 8\end{array}$ $\begin{array}{llllllll}4 & 5 & 3 & 6 & 2 & 1 & 7 & 8\end{array}$ $\begin{array}{llllllll}4 & 5 & 3 & 6 & 7 & 8 & 2 & 1\end{array}$ $\begin{array}{llllllll}4 & 5 & 6 & 7 & 3 & 2 & 1 & 8\end{array}$ $\begin{array}{llllllll}4 & 5 & 6 & 7 & 3 & 2 & 8 & 1\end{array}$ $\begin{array}{llllllll}4 & 5 & 6 & 7 & 8 & 3 & 2 & 1\end{array}$ $\begin{array}{llllllll}5 & 4 & 3 & 2 & 1 & 6 & 7 & 8\end{array}$ $\begin{array}{llllllll}5 & 4 & 3 & 2 & 6 & 7 & 1 & 8\end{array}$ $\begin{array}{llllllll}5 & 4 & 3 & 2 & 6 & 7 & 8 & 1\end{array}$ $\begin{array}{llllllll}5 & 4 & 6 & 3 & 2 & 1 & 7 & 8\end{array}$ $\begin{array}{llllllll}5 & 4 & 6 & 3 & 7 & 8 & 2 & 1\end{array}$ $\begin{array}{llllllll}6 & 7 & 5 & 4 & 3 & 8 & 2 & 1\end{array}$ $\begin{array}{llllllll}6 & 7 & 5 & 4 & 8 & 3 & 2 & 1\end{array}$ $\begin{array}{llllllll}6 & 7 & 8 & 5 & 4 & 3 & 2 & 1\end{array}$ $\begin{array}{llllllll}7 & 6 & 8 & 5 & 4 & 3 & 2 & 1\end{array}$ $\begin{array}{llllllll}7 & 6 & 5 & 8 & 4 & 3 & 2 & 1\end{array}$ $\begin{array}{llllllll}8 & 7 & 6 & 5 & 4 & 3 & 2 & 1\end{array}$ In all cases, Alice's sum is either an even number greater than 2 , or else 15 or 21 , thus Alice always wins. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="34"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 4. Find all pairs $(p, q)$ of prime numbers such that $$ 1+\frac{p^{q}-q^{p}}{p+q} $$ is a prime number. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. It is clear that $p \neq q$. We set $$ 1+\frac{p^{q}-q^{p}}{p+q}=r $$ and we have that $$ p^{q}-q^{p}=(r-1)(p+q) $$ From Fermat's Little Theorem we have $$ p^{q}-q^{p} \equiv-q \quad(\bmod p) $$ Since we also have that $$ (r-1)(p+q) \equiv-r q-q \quad(\bmod p) $$ from (3) we get that $$ r q \equiv 0 \quad(\bmod p) \Rightarrow p \mid q r $$ hence $p \mid r$, which means that $p=r$. Therefore, (3) takes the form $$ p^{q}-q^{p}=(p-1)(p+q) $$ We will prove that $p=2$. Indeed, if $p$ is odd, then from Fermat's Little Theorem we have $$ p^{q}-q^{p} \equiv p \quad(\bmod q) $$ and since $$ (p-1)(p+q) \equiv p(p-1) \quad(\bmod q) $$ we have $$ p(p-2) \equiv 0 \quad(\bmod q) \Rightarrow q|p(p-2) \Rightarrow q| p-2 \Rightarrow q \leq p-2n^{2}+n+2$. This means that $q \leq 5$ and the only solution is for $q=5$. Hence the only pair which satisfy the condition is $(p, q)=(2,5)$. Comment by the PSC. From the problem condition, we get that $p^{q}$ should be bigger than $q^{p}$, which gives $$ q \ln p>p \ln q \Longleftrightarrow \frac{\ln p}{p}>\frac{\ln q}{q} $$ The function $\frac{\ln x}{x}$ is decreasing for $x>e$, thus if $p$ and $q$ are odd primes, we obtain $q>p$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">(2,5)</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="35"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 2. Let $x, y, z$ be positive integers such that $x \neq y \neq z \neq x$. Prove that $$ (x+y+z)(x y+y z+z x-2) \geq 9 x y z $$ When does the equality hold? </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Since $x, y, z$ are distinct positive integers, the required inequality is symmetric and WLOG we can suppose that $x \geq y+1 \geq z+2$. We consider 2 possible cases: Case 1. $y \geq z+2$. Since $x \geq y+1 \geq z+3$ it follows that $$ (x-y)^{2} \geq 1, \quad(y-z)^{2} \geq 4, \quad(x-z)^{2} \geq 9 $$ which are equivalent to $$ x^{2}+y^{2} \geq 2 x y+1, \quad y^{2}+z^{2} \geq 2 y z+4, \quad x^{2}+z^{2} \geq 2 x z+9 $$ or otherwise $$ z x^{2}+z y^{2} \geq 2 x y z+z, \quad x y^{2}+x z^{2} \geq 2 x y z+4 x, \quad y x^{2}+y z^{2} \geq 2 x y z+9 y $$ Adding up the last three inequalities we have $$ x y(x+y)+y z(y+z)+z x(z+x) \geq 6 x y z+4 x+9 y+z $$ which implies that $(x+y+z)(x y+y z+z x-2) \geq 9 x y z+2 x+7 y-z$. Since $x \geq z+3$ it follows that $2 x+7 y-z \geq 0$ and our inequality follows. Case 2. $y=z+1$. Since $x \geq y+1=z+2$ it follows that $x \geq z+2$, and replacing $y=z+1$ in the required inequality we have to prove $$ (x+z+1+z)(x(z+1)+(z+1) z+z x-2) \geq 9 x(z+1) z $$ which is equivalent to $$ (x+2 z+1)\left(z^{2}+2 z x+z+x-2\right)-9 x(z+1) z \geq 0 $$ Doing easy algebraic manipulations, this is equivalent to prove $$ (x-z-2)(x-z+1)(2 z+1) \geq 0 $$ which is satisfied since $x \geq z+2$. The equality is achieved only in the Case 2 for $x=z+2$, so we have equality when $(x, y, z)=$ $(k+2, k+1, k)$ and all the permutations for any positive integer $k$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="36"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 3. Let $A B C$ be an acute triangle such that $A B \neq A C$, with circumcircle $\Gamma$ and circumcenter $O$. Let $M$ be the midpoint of $B C$ and $D$ be a point on $\Gamma$ such that $A D \perp B C$. Let $T$ be a point such that $B D C T$ is a parallelogram and $Q$ a point on the same side of $B C$ as $A$ such that $$ \angle B Q M=\angle B C A \quad \text { and } \quad \angle C Q M=\angle C B A $$ Let the line $A O$ intersect $\Gamma$ at $E,(E \neq A)$ and let the circumcircle of $\triangle E T Q$ intersect $\Gamma$ at point $X \neq E$. Prove that the points $A, M$, and $X$ are collinear. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Let $X^{\prime}$ be symmetric point to $Q$ in line $B C$. Now since $\angle C B A=\angle C Q M=\angle C X^{\prime} M$, $\angle B C A=\angle B Q M=\angle B X^{\prime} M$, we have $$ \angle B X^{\prime} C=\angle B X^{\prime} M+\angle C X^{\prime} M=\angle C B A+\angle B C A=180^{\circ}-\angle B A C $$ we have that $X^{\prime} \in \Gamma$. Now since $\angle A X^{\prime} B=\angle A C B=\angle M X^{\prime} B$ we have that $A, M, X^{\prime}$ are collinear. Note that since $$ \angle D C B=\angle D A B=90^{\circ}-\angle A B C=\angle O A C=\angle E A C $$ we get that $D B C E$ is an isosceles trapezoid. ![](https://cdn.mathpix.com/cropped/2024_06_05_7b55aeb0100cae01314ag-2.jpg?height=802&width=771&top_left_y=1478&top_left_x=677) Since $B D C T$ is a parallelogram we have $M T=M D$, with $M, D, T$ being collinear, $B D=C T$, and since $B D E C$ is an isosceles trapezoid we have $B D=C E$ and $M E=M D$. Since $$ \angle B T C=\angle B D C=\angle B E D, \quad C E=B D=C T \quad \text { and } \quad M E=M T $$ we have that $E$ and $T$ are symmetric with respect to the line $B C$. Now since $Q$ and $X^{\prime}$ are symmetric with respect to the line $B C$ as well, this means that $Q X^{\prime} E T$ is an isosceles trapezoid which means that $Q, X^{\prime}, E, T$ are concyclic. Since $X^{\prime} \in \Gamma$ this means that $X \equiv X^{\prime}$ and therefore $A, M, X$ are collinear. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="37"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 4. Consider a regular $2 n$-gon $P, A_{1} A_{2} \ldots A_{2 n}$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We color the sides of $P$ in 3 different colors (ignore the vertices of $P$, we consider them colorless), such that every side is colored in exactly one color, and each color is used at least once. Moreover, from every point in the plane external to $P$, points of at most 2 different colors on $P$ can be seen. Find the number of distinct such colorings of $P$ (two colorings are considered distinct if at least one of the sides is colored differently). </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution Answer: For $n=2$, the answer is 36 ; for $n=3$, the answer is 30 and for $n \geq 4$, the answer is $6 n$. Lemma 1. Given a regular $2 n$-gon in the plane and a sequence of $n$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n}$ there is an external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n$. Proof. It is obvious that for a semi-circle $S$, there is a point $R$ in the plane far enough on the bisector of its diameter such that almost the entire semi-circle can be seen from $R$. Now, it is clear that looking at the circumscribed circle around the $2 n$-gon, there is a semi-circle $S$ such that each $s_{i}$ either has both endpoints on it, or has an endpoint that's on the semi-circle, and is not on the semi-circle's end. So, take $Q$ to be a point in the plane from which almost all of $S$ can be seen, clearly, the color of each $s_{i}$ can be seen from $Q$. Lemma 2. Given a regular $2 n$-gon in the plane, and a sequence of $n+1$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n+1}$ there is no external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n+1$. Proof. Since $s_{1}$ and $s_{n+1}$ are parallel opposite sides of the $2 n$-gon, they cannot be seen at the same time from an external point. For $n=2$, we have a square, so all we have to do is make sure each color is used. Two sides will be of the same color, and we have to choose which are these 2 sides, and then assign colors according to this choice, so the answer is $\binom{4}{2} .3 .2=36$. For $n=3$, we have a hexagon. Denote the sides as $a_{1}, a_{2}, \ldots q_{6}$, in that order. There must be 2 consecutive sides of different colors, say $a_{1}$ is red, $a_{2}$ is blue. We must have a green side, and only $a_{4}$ and $a_{5}$ can be green. We have 3 possibilities: 1) $a_{4}$ is green, $a_{5}$ is not. So, $a_{3}$ must be blue and $a_{5}$ must be blue (by elimination) and $a_{6}$ must be blue, so we get a valid coloring. 2) Both $a_{4}$ and $a_{5}$ are green, thus $a_{6}$ must be red and $a_{5}$ must be blue, and we get the coloring rbbggr. 3) $a_{5}$ is green, $a_{4}$ is not. Then $a_{6}$ must be red. Subsequently, $a_{4}$ must be red (we assume it is not green). It remains that $a_{3}$ must be red, and the coloring is rbrrgr. Thus, we have 2 kinds of configurations: i) 2 opposite sides have 2 opposite colors and all other sides are of the third color. This can happen in 3.(3.2.1) $=18$ ways (first choosing the pair of opposite sides, then assigning colors), ii) 3 pairs of consecutive sides, each pair in one of the 3 colors. This can happen in $2.6=12$ ways (2 partitioning into pairs of consecutive sides, for each partitioning, 6 ways to assign the colors). Thus, for $n=3$, the answer is $18+12=30$. Finally, let's address the case $n \geq 4$. The important thing now is that any 4 consecutive sides can be seen from an external point, by Lemma 1 . Denote the sides as $a_{1}, a_{2}, \ldots, a_{2 n}$. Again, there must be 2 adjacent sides that are of different colors, say $a_{1}$ is blue and $a_{2}$ is red. We must have a green side, and by Lemma 1 , that can only be $a_{n+1}$ or $a_{n+2}$. So, we have 2 cases: Case 1: $a_{n+1}$ is green, so $a_{n}$ must be red (cannot be green due to Lemma 1 applied to $a_{1}, a_{2}, \ldots, a_{n}$, cannot be blue for the sake of $a_{2}, \ldots, a_{n+1}$. If $a_{n+2}$ is red, so are $a_{n+3}, \ldots, a_{2 n}$, and we get a valid coloring: $a_{1}$ is blue, $a_{n+1}$ is green, and all the others are red. If $a_{n+2}$ is green: a) $a_{n+3}$ cannot be green, because of $a_{2}, a_{1}, a_{2 n} \ldots, a_{n+3}$. b) $a_{n+3}$ cannot be blue, because the 4 adjacent sides $a_{n}, \ldots, a_{n+3}$ can be seen (this is the case that makes the separate treatment of $n \geq 4$ necessary) c) $a_{n+3}$ cannot be red, because of $a_{1}, a_{2 n}, \ldots, a_{n+2}$. So, in the case that $a_{n+2}$ is also green, we cannot get a valid coloring. Case 2: $a_{n+2}$ is green is treated the same way as Case 1. This means that the only valid configuration for $n \geq 4$ is having 2 opposite sides colored in 2 different colors, and all other sides colored in the third color. This can be done in $n .3 .2=6 n$ ways. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">6n</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="38"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 1. Find all prime numbers $a, b, c$ and positive integers $k$ which satisfy the equation $$ a^{2}+b^{2}+16 \cdot c^{2}=9 \cdot k^{2}+1 $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"># Solution: The relation $9 \cdot k^{2}+1 \equiv 1(\bmod 3)$ implies $$ a^{2}+b^{2}+16 \cdot c^{2} \equiv 1(\bmod 3) \Leftrightarrow a^{2}+b^{2}+c^{2} \equiv 1(\bmod 3) $$ Since $a^{2} \equiv 0,1(\bmod 3), \quad b^{2} \equiv 0,1(\bmod 3), c^{2} \equiv 0,1(\bmod 3)$, we have: | $a^{2}$ | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | $b^{2}$ | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | | $c^{2}$ | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | | $a^{2}+b^{2}+c^{2}$ | 0 | 1 | 1 | 2 | 1 | 2 | 2 | 0 | From the previous table it follows that two of three prime numbers $a, b, c$ are equal to 3 . Case 1. $a=b=3$ We have $$ \begin{aligned} & a^{2}+b^{2}+16 \cdot c^{2}=9 \cdot k^{2}+1 \Leftrightarrow 9 \cdot k^{2}-16 \cdot c^{2}=17 \Leftrightarrow(3 k-4 c) \cdot(3 k+4 c)=17, \\ & \Leftrightarrow\left\{\begin{array} { l } { 3 k - 4 c = 1 , } \\ { 3 k + 4 c = 1 7 , } \end{array} \Leftrightarrow \left\{\begin{array}{l} c=2, \\ k=3, \end{array} \text { and } \quad(a, b, c, k)=(3,3,2,3) .\right.\right. \end{aligned} $$ Case 2. $c=3$ If $\left(3, b_{0}, c, k\right)$ is a solution of the given equation, then $\left(b_{0}, 3, c, k\right)$ is a solution too. Let $a=3$. We have $$ a^{2}+b^{2}+16 \cdot c^{2}=9 \cdot k^{2}+1 \Leftrightarrow 9 \cdot k^{2}-b^{2}=152 \Leftrightarrow(3 k-b) \cdot(3 k+b)=152 . $$ Both factors shall have the same parity and we obtain only 2 cases: - $\left\{\begin{array}{l}3 k-b=2, \\ 3 k+b=76,\end{array} \Leftrightarrow\left\{\begin{array}{l}b=37, \\ k=13,\end{array}\right.\right.$ and $(a, b, c, k)=(3,37,3,13)$; - $\left\{\begin{array}{l}3 k-b=4, \\ 3 k+b=38,\end{array} \Leftrightarrow\left\{\begin{array}{l}b=17, \\ k=7,\end{array}\right.\right.$ and $(a, b, c, k)=(3,17,3,7)$. So, the given equation has 5 solutions: $\{(37,3,3,13),(17,3,3,7),(3,37,3,13),(3,17,3,7),(3,3,2,3)\}$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">(37,3,3,13),(17,3,3,7),(3,37,3,13),(3,17,3,7),(3,3,2,3)</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="39"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 2. Let $a, b, c$ be positive real numbers such that $a+b+c=3$. Find the minimum value of the expression $$ A=\frac{2-a^{3}}{a}+\frac{2-b^{3}}{b}+\frac{2-c^{3}}{c} $$ ![](https://cdn.mathpix.com/cropped/2024_06_05_f56efd4e6fb711c0f78eg-2.jpg?height=348&width=477&top_left_y=109&top_left_x=241) $19^{\text {th }}$ Junior Balkan Mathematical Olympiad June 24-29, 2015, Belgrade, Serbia </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution: We can rewrite $A$ as follows: $$ \begin{aligned} & A=\frac{2-a^{3}}{a}+\frac{2-b^{3}}{b}+\frac{2-c^{3}}{c}=2\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)-a^{2}-b^{2}-c^{2}= \\ & 2\left(\frac{a b+b c+c a}{a b c}\right)-\left(a^{2}+b^{2}+c^{2}\right)=2\left(\frac{a b+b c+c a}{a b c}\right)-\left((a+b+c)^{2}-2(a b+b c+c a)\right)= \\ & 2\left(\frac{a b+b c+c a}{a b c}\right)-(9-2(a b+b c+c a))=2\left(\frac{a b+b c+c a}{a b c}\right)+2(a b+b c+c a)-9= \\ & 2(a b+b c+c a)\left(\frac{1}{a b c}+1\right)-9 \end{aligned} $$ Recall now the well-known inequality $(x+y+z)^{2} \geq 3(x y+y z+z x)$ and set $x=a b, y=b c, z=c a$, to obtain $(a b+b c+c a)^{2} \geq 3 a b c(a+b+c)=9 a b c$, where we have used $a+b+c=3$. By taking the square roots on both sides of the last one we obtain: $$ a b+b c+c a \geq 3 \sqrt{a b c} $$ Also by using AM-GM inequality we get that $$ \frac{1}{a b c}+1 \geq 2 \sqrt{\frac{1}{a b c}} $$ Multiplication of (1) and (2) gives: $$ (a b+b c+c a)\left(\frac{1}{a b c}+1\right) \geq 3 \sqrt{a b c} \cdot 2 \sqrt{\frac{1}{a b c}}=6 $$ So $A \geq 2 \cdot 6-9=3$ and the equality holds if and only if $a=b=c=1$, so the minimum value is 3. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">3</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="40"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem 3. Let $\triangle A B C$ be an acute triangle. The lines $l_{1}, l_{2}$ are perpendicular to $A B$ at the points $A, B$ respectively. The perpendicular lines from the midpoint $M$ of $A B$ to the sides of the triangle $A C, B C$ intersect the lines $l_{1}, l_{2}$ at the points $E, F$, respectively. If $D$ is the intersection point of $E F$ and $M C$, prove that $$ \angle A D B=\angle E M F $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution: Let $H, G$ be the points of intersection of $M E, M F$ with $A C, B C$ respectively. From the similarity of triangles $\triangle M H A$ and $\triangle M A E$ we get $\frac{M H}{M A}=\frac{M A}{M E}$, thus $$ M A^{2}=M H \cdot M E $$ Similarly, from the similarity of triangles $\triangle M B G$ and $\triangle M F B$ we get $\frac{M B}{M F}=\frac{M G}{M B}$, thus $$ M B^{2}=M F \cdot M G $$ Since $M A=M B$, from (1), (2), we conclude that the points $E, H, G, F$ are concyclic. ![](https://cdn.mathpix.com/cropped/2024_06_05_f56efd4e6fb711c0f78eg-3.jpg?height=1040&width=1220&top_left_y=110&top_left_x=226) Therefore, we get that $\angle F E H=\angle F E M=\angle H G M$. Also, the quadrilateral $C H M G$ is cyclic, so $\angle C M H=\angle H G C$. We have $$ \angle F E H+\angle C M H=\angle H G M+\angle H G C=90^{\circ} $$ thus $C M \perp E F$. Now, from the cyclic quadrilaterals $F D M B$ and $E A M D$, we get that $\angle D F M=\angle D B M$ and $\angle D E M=\angle D A M$. Therefore, the triangles $\triangle E M F$ and $\triangle A D B$ are similar, so $\angle A D B=\angle E M F$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="41"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Problem 4. An $L$-figure is one of the following four pieces, each consisting of three unit squares: ![](https://cdn.mathpix.com/cropped/2024_06_05_f56efd4e6fb711c0f78eg-3.jpg?height=208&width=1008&top_left_y=1692&top_left_x=524) A $5 \times 5$ board, consisting of 25 unit squares, a positive integer $k \leq 25$ and an unlimited supply $L$-figures are given. Two players, $\boldsymbol{A}$ and $\boldsymbol{B}$, play the following game: starting with $\boldsymbol{A}$ they alternatively mark a previously unmarked unit square until they marked a total of $k$ unit squares. We say that a placement of $L$-figures on unmarked unit squares is called good if the $L$-figure do not overlap and each of them covers exactly three unmarked unit squares of the board. $\boldsymbol{B}$ wins if every $\boldsymbol{g o o d}$ placement of $L$-figures leaves uncovered at least three unmarked unit squares. Determine the minimum value of $k$ for which $\boldsymbol{B}$ has a winning strategy. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution: We will show that player $\boldsymbol{A}$ wins if $k=1,2,3$, but player $\boldsymbol{B}$ wins if $k=4$. Thus the smallest $k$ for which $\boldsymbol{B}$ has a winning strategy exists and is equal to 4 . If $k=1$, player $\boldsymbol{A}$ marks the upper left corner of the square and then fills it as follows. ![](https://cdn.mathpix.com/cropped/2024_06_05_f56efd4e6fb711c0f78eg-4.jpg?height=356&width=497&top_left_y=105&top_left_x=223) ## $19^{\text {th }}$ Junior Balkan Mathematical Olympiad June 24-29, 2015, Belgrade, Serbia![](https://cdn.mathpix.com/cropped/2024_06_05_f56efd4e6fb711c0f78eg-4.jpg?height=389&width=397&top_left_y=568&top_left_x=835) If $k=2$, player $\boldsymbol{A}$ marks the upper left corner of the square. Whatever square player $\boldsymbol{B}$ marks, then player $\boldsymbol{A}$ can fill in the square in exactly the same pattern as above except that he doesn't put the $L$-figure which covers the marked square of $\boldsymbol{B}$. Player $\boldsymbol{A}$ wins because he has left only two unmarked squares uncovered. For $k=3$, player $\boldsymbol{A}$ wins by following the same strategy. When he has to mark a square for the second time, he marks any yet unmarked square of the $L$-figure that covers the marked square of $\boldsymbol{B}$. Let us now show that for $k=4$ player $\boldsymbol{B}$ has a winning strategy. Since there will be 21 unmarked squares, player $\boldsymbol{A}$ will need to cover all of them with seven $L$-figures. We can assume that in his first move, player $\boldsymbol{A}$ does not mark any square in the bottom two rows of the chessboard (otherwise just rotate the chessboard). In his first move player $\boldsymbol{B}$ marks the square labeled 1 in the following figure. ![](https://cdn.mathpix.com/cropped/2024_06_05_f56efd4e6fb711c0f78eg-4.jpg?height=352&width=349&top_left_y=1623&top_left_x=859) If player $\boldsymbol{A}$ in his next move does not mark any of the squares labeled 2,3 and 4 then player $\boldsymbol{B}$ marks the square labeled 3 . Player $\boldsymbol{B}$ wins as the square labeled 2 is left unmarked but cannot be covered with an $L$-figure. If player $\boldsymbol{A}$ in his next move marks the square labeled 2, then player $\boldsymbol{B}$ marks the square labeled 5. Player $\boldsymbol{B}$ wins as the square labeled 3 is left unmarked but cannot be covered with an $L$-figure. Finally, if player $\boldsymbol{A}$ in his next move marks one of the squares labeled 3 or 4, player $\boldsymbol{B}$ marks the other of these two squares. Player $\boldsymbol{B}$ wins as the square labeled 2 is left unmarked but cannot be covered with an $L$-figure. Since we have covered all possible cases, player $\boldsymbol{B}$ wins when $k=4$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">4</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Incomplete</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="42"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> A1. Let $a, b, c$ be positive real numbers such that $a+b+c+a b+b c+c a+a b c=7$. Prove that $$ \sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} \geq 6 $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. First we see that $x^{2}+y^{2}+1 \geq x y+x+y$. Indeed, this is equivalent to $$ (x-y)^{2}+(x-1)^{2}+(y-1)^{2} \geq 0 $$ Therefore $$ \begin{aligned} & \sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} \\ \geq & \sqrt{a b+a+b+1}+\sqrt{b c+b+c+1}+\sqrt{c a+c+a+1} \\ = & \sqrt{(a+1)(b+1)}+\sqrt{(b+1)(a+1)}+\sqrt{(c+1)(a+1)} \end{aligned} $$ It follows from the AM-GM inequality that $$ \begin{aligned} & \sqrt{(a+1)(b+1)}+\sqrt{(b+1)(a+1)}+\sqrt{(c+1)(a+1)} \\ \geq & 3 \sqrt[3]{\sqrt{(a+1)(b+1)} \cdot \sqrt{(b+1)(a+1)} \cdot \sqrt{(c+1)(a+1)}} \\ = & 3 \sqrt[3]{(a+1)(b+1)(c+1)} \end{aligned} $$ On the other hand, the given condition is equivalent to $(a+1)(b+1)(c+1)=8$ and we get the desired inequality. Obviously, equality is attained if and only if $a=b=c=1$. Remark. The condition of positivity of $a, b, c$ is superfluous and the equality $\cdots=7$ can be replaced by the inequality $\cdots \geq 7$. Indeed, the above proof and the triangle inequality imply that $$ \begin{aligned} \sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} & \geq 3 \sqrt[3]{(|a|+1)(|b|+1)(|c|+1)} \\ & \geq 3 \sqrt[3]{|a+1| \cdot|b+1| \cdot|c+1|} \geq 6 \end{aligned} $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="43"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> A2. Let $a$ and $b$ be positive real numbers such that $3 a^{2}+2 b^{2}=3 a+2 b$. Find the minimum value of $$ A=\sqrt{\frac{a}{b(3 a+2)}}+\sqrt{\frac{b}{a(2 b+3)}} $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. By the Cauchy-Schwarz inequality we have that $$ 5\left(3 a^{2}+2 b^{2}\right)=5\left(a^{2}+a^{2}+a^{2}+b^{2}+b^{2}\right) \geq(3 a+2 b)^{2} $$ (or use that the last inequality is equivalent to $(a-b)^{2} \geq 0$ ). So, with the help of the given condition we get that $3 a+2 b \leq 5$. Now, by the AM-GM inequality we have that $$ A \geq 2 \sqrt{\sqrt{\frac{a}{b(3 a+2)}} \cdot \sqrt{\frac{b}{a(2 b+3)}}}=\frac{2}{\sqrt[4]{(3 a+2)(2 b+3)}} $$ Finally, using again the AM-GM inequality, we get that $$ (3 a+2)(2 b+3) \leq\left(\frac{3 a+2 b+5}{2}\right)^{2} \leq 25 $$ so $A \geq 2 / \sqrt{5}$ and the equality holds if and only if $a=b=1$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">\frac{2}{\sqrt{5}}</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Algebra</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="44"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> A3. Let $a, b, c, d$ be real numbers such that $0 \leq a \leq b \leq c \leq d$. Prove the inequality $$ a b^{3}+b c^{3}+c d^{3}+d a^{3} \geq a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2} $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. The inequality is equivalent to $$ \left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)^{2} \geq\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\right)^{2} $$ By the Cauchy-Schwarz inequality, $$ \left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\right) \geq\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\right)^{2} $$ Hence it is sufficient to prove that $$ \left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)^{2} \geq\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\right) $$ i.e. to prove $a b^{3}+b c^{3}+c d^{3}+d a^{3} \geq a^{3} b+b^{3} c+c^{3} d+d^{3} a$. This inequality can be written successively $$ a\left(b^{3}-d^{3}\right)+b\left(c^{3}-a^{3}\right)+c\left(d^{3}-b^{3}\right)+d\left(a^{3}-c^{3}\right) \geq 0 $$ or $$ (a-c)\left(b^{3}-d^{3}\right)-(b-d)\left(a^{3}-c^{3}\right) \geq 0 $$ which comes down to $$ (a-c)(b-d)\left(b^{2}+b d+d^{2}-a^{2}-a c-c^{2}\right) \geq 0 $$ The last inequality is true because $a-c \leq 0, b-d \leq 0$, and $\left(b^{2}-a^{2}\right)+(b d-a c)+\left(d^{2}-c^{2}\right) \geq 0$ as a sum of three non-negative numbers. The last inequality is satisfied with equality whence $a=b$ and $c=d$. Combining this with the equality cases in the Cauchy-Schwarz inequality we obtain the equality cases for the initial inequality: $a=b=c=d$. Remark. Instead of using the Cauchy-Schwarz inequality, once the inequality $a b^{3}+b c^{3}+c d^{3}+$ $d a^{3} \geq a^{3} b+b^{3} c+c^{3} d+d^{3} a$ is established, we have $2\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right) \geq\left(a b^{3}+b c^{3}+c d^{3}+\right.$ $\left.d a^{3}\right)+\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\right)=\left(a b^{3}+a^{3} b\right)+\left(b c^{3}+b^{3} c\right)+\left(c d^{3}+c^{3} d\right)+\left(d a^{3}+d^{3} a\right) \stackrel{A M-G M}{\geq}$ $2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} d^{2}+2 d^{2} a^{2}$ which gives the conclusion. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="45"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> A4. Let $x, y, z$ be three distinct positive integers. Prove that $$ (x+y+z)(x y+y z+z x-2) \geq 9 x y z $$ When does the equality hold? </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Since $x, y, z$ are distinct positive integers, the required inequality is symmetric and WLOG we can suppose that $x \geq y+1 \geq z+2$. We consider 2 possible cases: Case 1. $y \geq z+2$. Since $x \geq y+1 \geq z+3$ it follows that $$ (x-y)^{2} \geq 1, \quad(y-z)^{2} \geq 4, \quad(x-z)^{2} \geq 9 $$ which are equivalent to $$ x^{2}+y^{2} \geq 2 x y+1, \quad y^{2}+z^{2} \geq 2 y z+4, \quad x^{2}+z^{2} \geq 2 x z+9 $$ or otherwise $$ z x^{2}+z y^{2} \geq 2 x y z+z, \quad x y^{2}+x z^{2} \geq 2 x y z+4 x, \quad y x^{2}+y z^{2} \geq 2 x y z+9 y $$ Adding up the last three inequalities we have $$ x y(x+y)+y z(y+z)+z x(z+x) \geq 6 x y z+4 x+9 y+z $$ which implies that $(x+y+z)(x y+y z+z x-2) \geq 9 x y z+2 x+7 y-z$. Since $x \geq z+3$ it follows that $2 x+7 y-z \geq 0$ and our inequality follows. Case 2. $y=z+1$. Since $x \geq y+1=z+2$ it follows that $x \geq z+2$, and replacing $y=z+1$ in the required inequality we have to prove $$ (x+z+1+z)(x(z+1)+(z+1) z+z x-2) \geq 9 x(z+1) z $$ which is equivalent to $$ (x+2 z+1)\left(z^{2}+2 z x+z+x-2\right)-9 x(z+1) z \geq 0 $$ Doing easy algebraic manipulations, this is equivalent to prove $$ (x-z-2)(x-z+1)(2 z+1) \geq 0 $$ which is satisfied since $x \geq z+2$. The equality is achieved only in the Case 2 for $x=z+2$, so we have equality when $(x, y, z)=$ $(k+2, k+1, k)$ and all the permutations for any positive integer $k$. ## Combinatorics </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="46"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> C1. Consider a regular $2 n+1$-gon $P$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We want to color the sides of $P$ in 3 colors, such that every side is colored in exactly one color, and each color must be used at least once. Moreover, from every point in the plane external to $P$, at most 2 different colors on $P$ can be seen (ignore the vertices of $P$, we consider them colorless). Find the largest positive integer for which such a coloring is possible. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Answer: $n=1$ is clearly a solution, we can just color each side of the equilateral triangle in a different color, and the conditions are satisfied. We prove there is no larger $n$ that fulfills the requirements. Lemma 1. Given a regular $2 n+1$-gon in the plane, and a sequence of $n+1$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n+1}$ there is an external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n+1$. Proof. It is obvious that for a semi-circle $S$, there is a point $R$ in the plane far enough on the perpendicular bisector of the diameter of $S$ such that almost the entire semi-circle can be seen from $R$. Now, it is clear that looking at the circumscribed circle around the $2 n+1$-gon, there is a semi-circle $S$ such that each $s_{i}$ either has both endpoints on it, or has an endpoint that is on the semi-circle, and is not on the semicircle's end. So, take $Q$ to be a point in the plane from which almost all of $S$ can be seen, clearly, the color of each $s_{i}$ can be seen from $Q$. $\diamond$ Take $n \geq 2$, denote the sides $a_{1}, a_{2}, \ldots, a_{2 n+1}$ in that order, and suppose we have a coloring that satisfies the condition of the problem. Let's call the 3 colors red, green and blue. We must have 2 adjacent sides of different colors, say $a_{1}$ is red and $a_{2}$ is green. Then, by Lemma 1 : (i) We cannot have a blue side among $a_{1}, a_{2}, \ldots, a_{n+1}$. (ii) We cannot have a blue side among $a_{2}, a_{1}, a_{2 n+1}, \ldots, a_{n+3}$. We are required to have at least one blue side, and according to 1 ) and 2), that can only be $a_{n+2}$, so $a_{n+2}$ is blue. Now, applying Lemma 1 on the sequence of sides $a_{2}, a_{3}, \ldots, a_{n+2}$ we get that $a_{2}, a_{3}, \ldots, a_{n+1}$ are all green. Applying Lemma 1 on the sequence of sides $a_{1}, a_{2 n+1}, a_{2 n}, \ldots, a_{n+2}$ we get that $a_{2 n+1}, a_{2 n}, \ldots, a_{n+3}$ are all red. Therefore $a_{n+1}, a_{n+2}$ and $a_{n+3}$ are all of different colors, and for $n \geq 2$ they can all be seen from the same point according to Lemma 1 , so we have a contradiction. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">1</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="47"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> C2. Consider a regular $2 n$-gon $P$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We want to color the sides of $P$ in 3 colors, such that every side is colored in exactly one color, and each color must be used at least once. Moreover, from every point in the plane external to $P$, at most 2 different colors on $P$ can be seen (ignore the vertices of $P$, we consider them colorless). Find the number of distinct such colorings of $P$ (two colorings are considered distinct if at least one side is colored differently). </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Answer: For $n=2$, the answer is 36 ; for $n=3$, the answer is 30 and for $n \geq 4$, the answer is $6 n$. Lemma 1. Given a regular $2 n$-gon in the plane and a sequence of $n$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n}$ there is an external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n$. Proof. It is obvious that for a semi-circle $S$, there is a point $R$ in the plane far enough on the bisector of its diameter such that almost the entire semi-circle can be seen from $R$. Now, it is clear that looking at the circumscribed circle around the $2 n$-gon, there is a semi-circle $S$ such that each $s_{i}$ either has both endpoints on it, or has an endpoint that's on the semi-circle, and is not on the semi-circle's end. So, take $Q$ to be a point in the plane from which almost all of $S$ can be seen, clearly, the color of each $s_{i}$ can be seen from $Q$. Lemma 2. Given a regular $2 n$-gon in the plane, and a sequence of $n+1$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n+1}$ there is no external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n+1$. Proof. Since $s_{1}$ and $s_{n+1}$ are parallel opposite sides of the $2 n$-gon, they cannot be seen at the same time from an external point. For $n=2$, we have a square, so all we have to do is make sure each color is used. Two sides will be of the same color, and we have to choose which are these 2 sides, and then assign colors according to this choice, so the answer is $\binom{4}{2} \cdot 3 \cdot 2=36$. For $n=3$, we have a hexagon. Denote the sides as $a_{1}, a_{2}, \ldots q_{6}$, in that order. There must be 2 consecutive sides of different colors, say $a_{1}$ is red, $a_{2}$ is blue. We must have a green side, and only $a_{4}$ and $a_{5}$ can be green. We have 3 possibilities: 1) $a_{4}$ is green, $a_{5}$ is not. So, $a_{3}$ must be blue and $a_{5}$ must be blue (by elimination) and $a_{6}$ must be blue, so we get a valid coloring. 2) Both $a_{4}$ and $a_{5}$ are green, thus $a_{6}$ must be red and $a_{5}$ must be blue, and we get the coloring rbbggr. 3) $a_{5}$ is green, $a_{4}$ is not. Then $a_{6}$ must be red. Subsequently, $a_{4}$ must be red (we assume it is not green). It remains that $a_{3}$ must be red, and the coloring is rbrrgr. Thus, we have 2 kinds of configurations: i) 2 opposite sides have 2 opposite colors and all other sides are of the third color. This can happen in 3.(3.2.1) $=18$ ways (first choosing the pair of opposite sides, then assigning colors), ii) 3 pairs of consecutive sides, each pair in one of the 3 colors. This can happen in $2.6=12$ ways (2 partitioning into pairs of consecutive sides, for each partitioning, 6 ways to assign the colors). Thus, for $n=3$, the answer is $18+12=30$. Finally, let's address the case $n \geq 4$. The important thing now is that any 4 consecutive sides can be seen from an external point, by Lemma 1. Denote the sides as $a_{1}, a_{2}, \ldots, a_{2 n}$. Again, there must be 2 adjacent sides that are of different colors, say $a_{1}$ is blue and $a_{2}$ is red. We must have a green side, and by Lemma 1, that can only be $a_{n+1}$ or $a_{n+2}$. So, we have 2 cases: Case 1: $a_{n+1}$ is green, so $a_{n}$ must be red (cannot be green due to Lemma 1 applied to $a_{1}, a_{2}, \ldots, a_{n}$, cannot be blue for the sake of $a_{2}, \ldots, a_{n+1}$. If $a_{n+2}$ is red, so are $a_{n+3}, \ldots, a_{2 n}$, and we get a valid coloring: $a_{1}$ is blue, $a_{n+1}$ is green, and all the others are red. If $a_{n+2}$ is green: a) $a_{n+3}$ cannot be green, because of $a_{2}, a_{1}, a_{2 n} \ldots, a_{n+3}$. b) $a_{n+3}$ cannot be blue, because the 4 adjacent sides $a_{n}, \ldots, a_{n+3}$ can be seen (this is the case that makes the separate treatment of $n \geq 4$ necessary) c) $a_{n+3}$ cannot be red, because of $a_{1}, a_{2 n}, \ldots, a_{n+2}$. So, in the case that $a_{n+2}$ is also green, we cannot get a valid coloring. Case 2: $a_{n+2}$ is green is treated the same way as Case 1. This means that the only valid configuration for $n \geq 4$ is having 2 opposite sides colored in 2 different colors, and all other sides colored in the third color. This can be done in $n \cdot 3 \cdot 2=6 n$ ways. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">6n</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="48"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> C3. We have two piles with 2000 and 2017 coins respectively. Ann and Bob take alternate turns making the following moves: The player whose turn is to move picks a pile with at least two coins, removes from that pile $t$ coins for some $2 \leqslant t \leqslant 4$, and adds to the other pile 1 coin. The players can choose a different $t$ at each turn, and the player who cannot make a move loses. If Ann plays first determine which player has a winning strategy. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Denote the number of coins in the two piles by $X$ and $Y$. We say that the pair $(X, Y)$ is losing if the player who begins the game loses and that the pair $(X, Y)$ is winning otherwise. We shall prove that $(X, Y)$ is loosing if $X-Y \equiv 0,1,7 \bmod 8$, and winning if $X-Y \equiv 2,3,4,5,6 \bmod 8$. Lemma 1. If we have a winning pair $(X, Y)$ then we can always play in such a way that the other player is then faced with a losing pair. Proof of Lemma 1. Assume $X \geq Y$ and write $X=Y+8 k+\ell$ for some non-negative integer $k$ and some $\ell \in\{2,3,4,5,6\}$. If $\ell=2,3,4$ then we remove two coins from the first pile and add one coin to the second pile. If $\ell=5,6$ then we remove four coins from the first pile and add one coin to the second pile. In each case we then obtain loosing pair Lemma 2. If we are faced with a losing distribution then either we cannot play, or, however we play, the other player is faced with a winning distribution. Proof of Lemma 2. Without loss of generality we may assume that we remove $k$ coins from the first pile. The following table show the new difference for all possible values of $k$ and all possible differences $X-Y$. So however we move, the other player will be faced with a winning distribution. | $k \backslash X-Y$ | 0 | 1 | 7 | | :---: | :---: | :---: | :---: | | 2 | 5 | 6 | 4 | | 3 | 4 | 5 | 3 | | 4 | 3 | 4 | 2 | Since initially the coin difference is 1 mod 8 , by Lemmas 1 and 2 Bob has a winning strategy: He can play so that he is always faced with a winning distribution while Ann is always faced with a losing distribution. So Bob cannot lose. On the other hand the game finishes after at most 4017 moves, so Ann has to lose. ## Geometry </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="49"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> G1. Given a parallelogram $A B C D$. The line perpendicular to $A C$ passing through $C$ and the line perpendicular to $B D$ passing through $A$ intersect at point $P$. The circle centered at point $P$ and radius $P C$ intersects the line $B C$ at point $X,(X \neq C)$ and the line $D C$ at point $Y$, $(Y \neq C)$. Prove that the line $A X$ passes through the point $Y$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Denote the feet of the perpendiculars from $P$ to the lines $B C$ and $D C$ by $M$ and $N$ respectively and let $O=A C \cap B D$. Since the points $O, M$ and $N$ are midpoints of $C A, C X$ and $C Y$ respectively it suffices to prove that $M, N$ and $O$ are collinear. According to Menelaus's theorem for $\triangle B C D$ and points $M, N$ and $O$ we have to prove that ![](https://cdn.mathpix.com/cropped/2024_06_05_7db2aacb858e7f253ee0g-11.jpg?height=575&width=616&top_left_y=905&top_left_x=1226) $$ \frac{B M}{M C} \cdot \frac{C N}{N D} \cdot \frac{D O}{O B}=1 $$ Since $D O=O B$ the above simplifies to $\frac{B M}{C M}=\frac{D N}{C N}$. It follows from $B M=B C+C M$ and $D N=D C-C N=A B-C N$ that the last equality is equivalent to: $$ \frac{B C}{C M}+2=\frac{A B}{C N} $$ Denote by $S$ the foot of the perpendicular from $B$ to $A C$. Since $\Varangle B C S=\Varangle C P M=\varphi$ and $\Varangle B A C=\Varangle A C D=\Varangle C P N=\psi$ we conclude that $\triangle C B S \sim \triangle P C M$ and $\triangle A B S \sim \triangle P C N$. Therefore $$ \frac{C M}{B S}=\frac{C P}{B C} \text { and } \frac{C N}{B S}=\frac{C P}{A B} $$ and thus, $$ C M=\frac{C P . B S}{B C} \text { and } C N=\frac{C P . B S}{A B} $$ Now equality (1) becomes $A B^{2}-B C^{2}=2 C P . B S$. It follows from $$ A B^{2}-B C^{2}=A S^{2}-C S^{2}=(A S-C S)(A S+C S)=2 O S . A C $$ that $$ D C^{2}-B C^{2}=2 C P \cdot B S \Longleftrightarrow 2 O S \cdot A C=2 C P . B S \Longleftrightarrow O S \cdot A C=C P \cdot B S . $$ Since $\Varangle A C P=\Varangle B S O=90^{\circ}$ and $\Varangle C A P=\Varangle S B O$ we conclude that $\triangle A C P \sim \triangle B S O$. This implies $O S . A C=C P . B S$, which completes the proof. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="50"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> G2. Let $A B C$ be an acute triangle such that $A B$ is the shortest side of the triangle. Let $D$ be the midpoint of the side $A B$ and $P$ be an interior point of the triangle such that $$ \Varangle C A P=\Varangle C B P=\Varangle A C B $$ Denote by $M$ and $N$ the feet of the perpendiculars from $P$ to $B C$ and $A C$, respectively. Let $p$ be the line through $M$ parallel to $A C$ and $q$ be the line through $N$ parallel to $B C$. If $p$ and $q$ intersect at $K$ prove that $D$ is the circumcenter of triangle $M N K$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. If $\gamma=\Varangle A C B$ then $\Varangle C A P=\Varangle C B P=\Varangle A C B=\gamma$. Let $E=K N \cap A P$ and $F=K M \cap B P$. We show that points $E$ and $F$ are midpoints of $A P$ and $B P$, respectively. ![](https://cdn.mathpix.com/cropped/2024_06_05_7db2aacb858e7f253ee0g-13.jpg?height=545&width=1009&top_left_y=1137&top_left_x=539) Indeed, consider the triangle $A E N$. Since $K N \| B C$, we have $\Varangle E N A=\Varangle B C A=\gamma$. Moreover $\Varangle E A N=\gamma$ giving that triangle $A E N$ is isosceles, i.e. $A E=E N$. Next, consider the triangle $E N P$. Since $\Varangle E N A=\gamma$ we find that $$ \Varangle P N E=90^{\circ}-\Varangle E N A=90^{\circ}-\gamma $$ Now $\Varangle E P N=90^{\circ}-\gamma$ implies that the triangle $E N P$ is isosceles triangle, i.e. $E N=E P$. Since $A E=E N=E P$ point $E$ is the midpoint of $A P$ and analogously, $F$ is the midpoint of $B P$. Moreover, $D$ is also midpoint of $A B$ and we conclude that $D F P E$ is parallelogram. It follows from $D E \| A P$ and $K E \| B C$ that $\Varangle D E K=\Varangle C B P=\gamma$ and analogously $\Varangle D F K=\gamma$. We conclude that $\triangle E D N \cong \triangle F M D(E D=F P=F M, E N=E P=F D$ and $\Varangle D E N=$ $\left.\Varangle M F D=180^{\circ}-\gamma\right)$ and thus $N D=M D$. Therefore $D$ is a point on the perpendicular bisector of $M N$. Further, $$ \begin{aligned} \Varangle F D E & =\Varangle F P E=360^{\circ}-\Varangle B P M-\Varangle M P N-\Varangle N P A= \\ & =360^{\circ}-\left(90^{\circ}-\gamma\right)-\left(180^{\circ}-\gamma\right)-\left(90^{\circ}-\gamma\right)=3 \gamma \end{aligned} $$ It follows that $$ \begin{aligned} \Varangle M D N & =\Varangle F D E-\Varangle F D M-\Varangle E D N=\Varangle F D E-\Varangle E N D-\Varangle E D N= \\ & =\Varangle F D E-(\Varangle E N D+\Varangle E D N)=3 \gamma-\gamma=2 \gamma . \end{aligned} $$ Fianlly, $K M C N$ is parallelogram, i.e. $\Varangle M K N=\Varangle M C N=\gamma$. Therefore $D$ is a point on the perpendicular bisector of $M N$ and $\Varangle M D N=2 \Varangle M K N$, so $D$ is the circumcenter of $\triangle M N K$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="51"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem G3. Consider triangle $A B C$ such that $A B \leq A C$. Point $D$ on the arc $B C$ of the circumcirle of $A B C$ not containing point $A$ and point $E$ on side $B C$ are such that $$ \Varangle B A D=\Varangle C A E<\frac{1}{2} \Varangle B A C . $$ Let $S$ be the midpoint of segment $A D$. If $\Varangle A D E=\Varangle A B C-\Varangle A C B$ prove that $$ \Varangle B S C=2 \Varangle B A C $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Let the tangent to the circumcircle of $\triangle A B C$ at point $A$ intersect line $B C$ at $T$. Since $A B \leq A C$ we get that $B$ lies between $T$ and $C$. Since $\Varangle B A T=\Varangle A C B$ and $\Varangle A B T=\Varangle 180^{\circ}-\Varangle A B C$ we get $\Varangle E T A=\Varangle B T A=\Varangle A B C-\Varangle A C B=\Varangle A D E$ which gives that $A, E, D, T$ are concyclic. Since $$ \Varangle T D B+\Varangle B C A=\Varangle T D B+\Varangle B D A=\Varangle T D A=\Varangle A E T=\Varangle A C B+\Varangle E A C $$ this means $\Varangle T D B=\Varangle E A C=\Varangle D A B$ which means that $T D$ is tangent to the circumcircle of $\triangle A B C$ at point $D$. ![](https://cdn.mathpix.com/cropped/2024_06_05_7db2aacb858e7f253ee0g-15.jpg?height=524&width=740&top_left_y=1619&top_left_x=649) Using similar triangles $T A B$ and $T C A$ we get $$ \frac{A B}{A C}=\frac{T A}{T C} $$ Using similar triangles $T B D$ and $T D C$ we get $$ \frac{B D}{C D}=\frac{T D}{T C} $$ Using the fact that $T A=T D$ with (1) and (2) we get $$ \frac{A B}{A C}=\frac{B D}{C D} $$ Now since $\Varangle D A B=\Varangle C A E$ and $\Varangle B D A=\Varangle E C A$ we get that the triangles $D A B$ and $C A E$ are similar. Analogously, we get that triangles $C A D$ and $E A B$ are similar. These similarities give us $$ \frac{D B}{C E}=\frac{A B}{A E} \quad \text { and } \quad \frac{C D}{E B}=\frac{C A}{E A} $$ which, when combined with (3) give us $B E=C E$ giving $E$ is the midpoint of side $B C$. Using the fact that triangles $D A B$ and $C A E$ are similar with the fact that $E$ is the midpoint of $B C$ we get: $$ \frac{2 D S}{C A}=\frac{D A}{C A}=\frac{D B}{C E}=\frac{D B}{\frac{C B}{2}}=\frac{2 D B}{C B} $$ implying that $$ \frac{D S}{D B}=\frac{C A}{C B} $$ Since $\Varangle S D B=\Varangle A D B=\Varangle A C B$ we get from (4) that the triangles $S D B$ and $A C B$ are similar, giving us $\Varangle B S D=\Varangle B A C$. Analogously we get $\triangle S D C$ and $\triangle A B C$ are similar we get $\Varangle C S D=\Varangle C A B$. Combining the last two equalities we get $$ 2 \Varangle B A C=\Varangle B A C+\Varangle C A B=\Varangle C S D+\Varangle B S D=\Varangle C S B $$ This completes the proof. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">2\VarangleBAC=\VarangleBSC</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="52"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem G4. Let $A B C$ be a scalene triangle with circumcircle $\Gamma$ and circumcenter $O$. Let $M$ be the midpoint of $B C$ and $D$ be a point on $\Gamma$ such that $A D \perp B C$. Let $T$ be a point such that $B D C T$ is a parallelogram and $Q$ a point on the same side of $B C$ as $A$ such that $$ \Varangle B Q M=\Varangle B C A \quad \text { and } \quad \Varangle C Q M=\Varangle C B A $$ Let $A O$ intersect $\Gamma$ again at $E$ and let the circumcircle of $E T Q$ intersect $\Gamma$ at point $X \neq E$. Prove that the points $A, M$, and $X$ are collinear. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Let $X^{\prime}$ be symmetric point to $Q$ in line $B C$. Now since $\Varangle C B A=\Varangle C Q M=$ $\Varangle C X^{\prime} M, \Varangle B C A=\Varangle B Q M=\Varangle B X^{\prime} M$, we have $$ \Varangle B X^{\prime} C=\Varangle B X^{\prime} M+\Varangle C X^{\prime} M=\Varangle C B A+\Varangle B C A=180^{\circ}-\Varangle B A C $$ we have that $X^{\prime} \in \Gamma$. Now since $\Varangle A X^{\prime} B=\Varangle A C B=\Varangle M X^{\prime} B$ we have that $A, M, X^{\prime}$ are collinear. Note that since $$ \Varangle D C B=\Varangle D A B=90^{\circ}-\Varangle A B C=\Varangle O A C=\Varangle E A C $$ we get that $D B C E$ is an isosceles trapezoid. ![](https://cdn.mathpix.com/cropped/2024_06_05_7db2aacb858e7f253ee0g-18.jpg?height=772&width=727&top_left_y=1625&top_left_x=669) Since $B D C T$ is a parallelogram we have $M T=M D$, with $M, D, T$ being collinear, $B D=C T$, and since $B D E C$ is an isosceles trapezoid we have $B D=C E$ and $M E=M D$. Since $$ \Varangle B T C=\Varangle B D C=\Varangle B E D, \quad C E=B D=C T \quad \text { and } \quad M E=M T $$ we have that $E$ and $T$ are symmetric with respect to the line $B C$. Now since $Q$ and $X^{\prime}$ are symmetric with respect to the line $B C$ as well, this means that $Q X^{\prime} E T$ is an isosceles trapezoid which means that $Q, X^{\prime}, E, T$ are concyclic. Since $X^{\prime} \in \Gamma$ this means that $X \equiv X^{\prime}$ and therefore $A, M, X$ are collinear. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="53"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Problem G5. A point $P$ lies in the interior of the triangle $A B C$. The lines $A P, B P$, and $C P$ intersect $B C, C A$, and $A B$ at points $D, E$, and $F$, respectively. Prove that if two of the quadrilaterals $A B D E, B C E F, C A F D, A E P F, B F P D$, and $C D P E$ are concyclic, then all six are concyclic. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. We first prove the following lemma: Lemma 1. Let $A B C D$ be a convex quadrilateral and let $A B \cap C D=E$ and $B C \cap D A=F$. Then the circumcircles of triangles $A B F, C D F, B C E$ and $D A E$ all pass through a common point $P$. This point lies on line $E F$ if and only if $A B C D$ in concyclic. Proof. Let the circumcircles of $A B F$ and $B C F$ intersect at $P \neq B$. We have $$ \begin{aligned} \Varangle F P C & =\Varangle F P B+\Varangle B P C=\Varangle B A D+\Varangle B E C=\Varangle E A D+\Varangle A E D= \\ & =180^{\circ}-\Varangle A D E=180^{\circ}-\Varangle F D C \end{aligned} $$ which gives us $F, P, C$ and $D$ are concyclic. Similarly we have $$ \begin{aligned} \Varangle A P E & =\Varangle A P B+\Varangle B P E=\Varangle A F B+\Varangle B C D=\Varangle D F C+\Varangle F C D= \\ & =180^{\circ}-\Varangle F D C=180^{\circ}-\Varangle A D E \end{aligned} $$ which gives us $E, P, A$ and $D$ are concyclic. Since $\Varangle F P E=\Varangle F P B+\Varangle E P B=\Varangle B A D+$ $\Varangle B C D$ we get that $\Varangle F P E=180^{\circ}$ if and only if $\Varangle B A D+\Varangle B C D=180^{\circ}$ which completes the lemma. We now divide the problem into cases: Case 1: $A E P F$ and $B F E C$ are concyclic. Here we get that $$ 180^{\circ}=\Varangle A E P+\Varangle A F P=360^{\circ}-\Varangle C E B-\Varangle B F C=360^{\circ}-2 \Varangle C E B $$ and here we get that $\Varangle C E B=\Varangle C F B=90^{\circ}$, from here it follows that $P$ is the ortocenter of $\triangle A B C$ and that gives us $\Varangle A D B=\Varangle A D C=90^{\circ}$. Now the quadrilaterals $C E P D$ and $B D P F$ are concyclic because $$ \Varangle C E P=\Varangle C D P=\Varangle P D B=\Varangle P F B=90^{\circ} . $$ Quadrilaterals $A C D F$ and $A B D E$ are concyclic because $$ \Varangle A E B=\Varangle A D B=\Varangle A D C=\Varangle A F C=90^{\circ} $$ Case 2: $A E P F$ and $C E P D$ are concyclic. Now by lemma 1 applied to the quadrilateral $A E P F$ we get that the circumcircles of $C E P, C A F, B P F$ and $B E A$ intersect at a point on $B C$. Since $D \in B C$ and $C E P D$ is concyclic we get that $D$ is the desired point and it follows that $B D P F, B A E D, C A F D$ are all concylic and now we can finish same as Case 1 since $A E D B$ and $C E P D$ are concyclic. Case 3: $A E P F$ and $A E D B$ are concyclic. We apply lemma 1 as in Case 2 on the quadrilateral $A E P F$. From the lemma we get that $B D P F, C E P D$ and $C A F D$ are concylic and we finish off the same as in Case 1. Case 4: $A C D F$ and $A B D E$ are concyclic. We apply lemma 1 on the quadrilateral $A E P F$ and get that the circumcircles of $A C F, E C P, P F B$ and $B A E$ intersect at one point. Since this point is $D$ (because $A C D F$ and $A B D E$ are concyclic) we get that $A E P F, C E P D$ and $B F P D$ are concylic. We now finish off as in Case 1. These four cases prove the problem statement. Remark. A more natural approach is to solve each of the four cases by simple angle chasing. ## Number Theory </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="54"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> NT1. Determine all sets of six consecutive positive integers such that the product of two of them, added to the the product of other two of them is equal to the product of the remaining two numbers. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Exactly two of the six numbers are multiples of 3 and these two need to be multiplied together, otherwise two of the three terms of the equality are multiples of 3 but the third one is not. Let $n$ and $n+3$ denote these multiples of 3 . Two of the four remaining numbers give remainder 1 when divided by 3 , while the other two give remainder 2 , so the two other products are either $\equiv 1 \cdot 1=1(\bmod 3)$ and $\equiv 2 \cdot 2 \equiv 1(\bmod 3)$, or they are both $\equiv 1 \cdot 2 \equiv 2(\bmod 3)$. In conclusion, the term $n(n+3)$ needs to be on the right hand side of the equality. Looking at parity, three of the numbers are odd, and three are even. One of $n$ and $n+3$ is odd, the other even, so exactly two of the other numbers are odd. As $n(n+3)$ is even, the two remaining odd numbers need to appear in different terms. We distinguish the following cases: I. The numbers are $n-2, n-1, n, n+1, n+2, n+3$. The product of the two numbers on the RHS needs to be larger than $n(n+3)$. The only possibility is $(n-2)(n-1)+n(n+3)=(n+1)(n+2)$ which leads to $n=3$. Indeed, $1 \cdot 2+3 \cdot 6=4 \cdot 5$ II. The numbers are $n-1, n, n+1, n+2, n+3, n+4$. As $(n+4)(n-1)+n(n+3)=(n+1)(n+2)$ has no solutions, $n+4$ needs to be on the RHS, multiplied with a number having a different parity, so $n-1$ or $n+1$. $(n+2)(n-1)+n(n+3)=(n+1)(n+4)$ leads to $n=3$. Indeed, $2 \cdot 5+3 \cdot 6=4 \cdot 7$. $(n+2)(n+1)+n(n+3)=(n-1)(n+4)$ has no solution. III. The numbers are $n, n+1, n+2, n+3, n+4, n+5$. We need to consider the following situations: $(n+1)(n+2)+n(n+3)=(n+4)(n+5)$ which leads to $n=6$; indeed $7 \cdot 8+6 \cdot 9=10 \cdot 11$; $(n+2)(n+5)+n(n+3)=(n+1)(n+4)$ obviously without solutions, and $(n+1)(n+4)+n(n+3)=(n+2)(n+5)$ which leads to $n=2$ (not a multiple of 3 ). In conclusion, the problem has three solutions: $$ 1 \cdot 2+3 \cdot 6=4 \cdot 5, \quad 2 \cdot 5+3 \cdot 6=4 \cdot 7, \quad \text { and } \quad 7 \cdot 8+6 \cdot 9=10 \cdot 11 $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">1\cdot2+3\cdot6=4\cdot5,\quad2\cdot5+3\cdot6=4\cdot7,\quad7\cdot8+6\cdot9=10\cdot11</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Incomplete</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="55"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> NT3. Find all pairs of positive integers $(x, y)$ such that $2^{x}+3^{y}$ is a perfect square. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. In order for the expression $2^{x}+3^{y}$ to be a perfect square, a positive integer $t$ such that $2^{x}+3^{y}=t^{2}$ should exist. Case 1. If $x$ is even, then there exists a positive integer $z$ such that $x=2 z$. Then $$ \left(t-2^{z}\right)\left(t+2^{z}\right)=3^{y} $$ Since $t+2^{z}-\left(t-2^{z}\right)=2^{z+1}$, which implies $g c d\left(t-2^{z}, t+2^{z}\right) \mid 2^{z+1}$, it follows that $\operatorname{gcd}\left(t-2^{z}, t+\right.$ $\left.2^{z}\right)=1$, hence $t-2^{z}=1$ and $t+2^{z}=3^{y}$, so we have $2^{z+1}+1=3^{y}$. For $z=1$ we have $5=3^{y}$ which clearly have no solution. For $z \geq 2$ we have (modulo 4) that $y$ is even. Let $y=2 k$. Then $2^{z+1}=\left(3^{k}-1\right)\left(3^{k}+1\right)$ which is possible only when $3^{k}-1=2$, i.e. $k=1, y=2$, which implies that $t=5$. So the pair $(4,2)$ is a solution to our problem. Case 2. If $y$ is even, then there exists a positive integer $w$ such that $y=2 w$, and $$ \left(t-3^{w}\right)\left(t+3^{w}\right)=2^{x} $$ Since $t+3^{w}-\left(t-3^{w}\right)=2 \cdot 3^{w}$, we have $\operatorname{gcd}\left(t-2^{z}, t+2^{z}\right) \mid 2 \cdot 3^{w}$, which means that $g c d(t-$ $\left.3^{w}, t+3^{w}\right)=2$. Hence $t-3^{w}=2$ and $t+3^{w}=2^{x-1}$. So we have $$ 2 \cdot 3^{w}+2=2^{x-1} \Rightarrow 3^{w}+1=2^{x-2} $$ Here we see modulo 3 that $x-2$ is even. Let $x-2=2 m$, then $3^{w}=\left(2^{m}-1\right)\left(2^{m}+1\right)$, whence $m=1$ since $\operatorname{gcd}\left(2^{m}-1,2^{m}+1\right)=1$. So we arrive again to the solution $(4,2)$. Case 3. Let $x$ and $y$ be odd. For $x \geq 3$ we have $2^{x}+3^{y} \equiv 3(\bmod 4)$ while $t^{2} \equiv 0,1(\bmod 4)$, a contradiction. For $x=1$ we have $2+3^{y}=t^{2}$. For $y \geq 2$ we have $2+3^{y} \equiv 2(\bmod 9)$ while $t^{2} \equiv 0,1,4,7(\bmod 9)$. For $y=1$ we have $5=2+3=t^{2}$ clearly this doesn't have solution. Note. The proposer's solution used Zsigmondy's theorem in the final steps of cases 1 and 2 . </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">(4,2)</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="56"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> NT4. Solve in nonnegative integers the equation $5^{t}+3^{x} 4^{y}=z^{2}$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. If $x=0$ we have $$ z^{2}-2^{2 y}=5^{t} \Longleftrightarrow\left(z+2^{y}\right)\left(z-2^{y}\right)=5^{t} $$ Putting $z+2^{y}=5^{a}$ and $z-2^{y}=5^{b}$ with $a+b=t$ we get $5^{a}-5^{b}=2^{y+1}$. This gives us $b=0$ and now we have $5^{t}-1=2^{y+1}$. If $y \geq 2$ then consideration by modulo 8 gives $2 \mid t$. Putting $t=2 s$ we get $\left(5^{s}-1\right)\left(5^{s}+1\right)=2^{y+1}$. This means $5^{s}-1=2^{c}$ and $5^{s}+1=2^{d}$ with $c+d=y+1$. Subtracting we get $2=2^{d}-2^{c}$. Then we have $c=1, d=2$, but the equation $5^{s}-1=2$ has no solutions over nonnegative integers. Therefore so $y \geq 2$ in this case gives us no solutions. If $y=0$ we get again $5^{t}-1=2$ which again has no solutions in nonnegative integers. If $y=1$ we get $t=1$ and $z=3$ which gives us the solution $(t, x, y, z)=(1,0,1,3)$. Now if $x \geq 1$ then by modulo 3 we have $2 \mid t$. Putting $t=2 s$ we get $$ 3^{x} 4^{y}=z^{2}-5^{2 s} \Longleftrightarrow 3^{x} 4^{y}=\left(z+5^{s}\right)\left(z-5^{s}\right) $$ Now we have $z+5^{s}=3^{m} 2^{k}$ and $z-5^{s}=3^{n} 2^{l}$, with $k+l=2 y$ and $m+n=x \geq 1$. Subtracting we get $$ 2.5^{s}=3^{m} 2^{k}-3^{n} 2^{l} $$ Here we get that $\min \{m, n\}=0$. We now have a couple of cases. Case 1. $k=l=0$. Now we have $n=0$ and we get the equation $2.5^{s}=3^{m}-1$. From modulo 4 we get that $m$ is odd. If $s \geq 1$ we get modulo 5 that $4 \mid m$, a contradiction. So $s=0$ and we get $m=1$. This gives us $t=0, x=1, y=0, z=2$. Case 2. $\min \{k, l\}=1$. Now we deal with two subcases: Case 2a. $l>k=1$. We get $5^{s}=3^{m}-3^{n} 2^{l-1}$. Since $\min \{m, n\}=0$, we get that $n=0$. Now the equation becomes $5^{s}=3^{m}-2^{l-1}$. Note that $l-1=2 y-2$ is even. By modulo 3 we get that $s$ is odd and this means $s \geq 1$. Now by modulo 5 we get $3^{m} \equiv 2^{2 y-2} \equiv 1,-1(\bmod 5)$. Here we get that $m$ is even as well, so we write $m=2 q$. Now we get $5^{s}=\left(3^{q}-2^{y-1}\right)\left(3^{q}+2^{y-1}\right)$. Therefore $3^{q}-2^{y-1}=5^{v}$ and $3^{q}+2^{y-1}=5^{u}$ with $u+v=s$. Then $2^{y}=5^{u}-5^{v}$, whence $v=0$ and we have $3^{q}-2^{y-1}=1$. Plugging in $y=1,2$ we get the solution $y=2, q=1$. This gives us $m=2, s=1, n=0, x=2, t=2$ and therefore $z=13$. Thus we have the solution $(t, x, y, z)=(2,2,2,13)$. If $y \geq 3$ we get modulo 4 that $q, q=2 r$. Then $\left(3^{r}-1\right)\left(3^{r}+1\right)=2^{y-1}$. Putting $3^{r}-1=2^{e}$ and $3^{r}+1=2^{f}$ with $e+f=y-1$ and subtracting these two and dividing by 2 we get $2^{f-1}-2^{e-1}=1$, whence $e=1, f=2$. Therefore $r=1, q=2, y=4$. Now since $2^{4}=5^{u}-1$ does not have a solution, it follows that there are no more solutions in this case. Case $2 b . \quad k>l=1$. We now get $5^{s}=3^{m} 2^{k-1}-3^{n}$. By modulo 4 (which we can use since $0<k-1=2 y-2)$ we get $3^{n} \equiv-1(\bmod 4)$ and therefore $n$ is odd. Now since $\min \{m, n\}=0$ we get that $m=0,0+n=m+n=x \geq 1$. The equation becomes $5^{s}=2^{2 y-2}-3^{x}$. By modulo 3 we see that $s$ is even. We now put $s=2 g$ and obtain $\left(2^{y-1}-5^{g}\right)\left(5^{g}+2^{y-1}\right)=3^{x}$. Putting $2^{y-1}-5^{g}=3^{h}, 2^{y-1}+5^{g}=3^{i}$, where $i+h=x$, and subtracting the equations we get $3^{i}-3^{h}=2^{y}$. This gives us $h=0$ and now we are solving the equation $3^{x}+1=2^{y}$. The solution $x=0, y=1$ gives $1-5^{g}=1$ without solution. If $x \geq 1$ then by modulo 3 we get that $y$ is even. Putting $y=2 y_{1}$ we obtain $3^{x}=\left(2^{y_{1}}-1\right)\left(2^{y_{1}}+1\right)$. Putting $2^{y_{1}}-1=3^{x_{1}}$ and $2^{y_{1}}+1=3^{x_{2}}$ and subtracting we get $3^{x_{2}}-3^{x_{1}}=2$. This equation gives us $x_{1}=0, x_{2}=1$. Then $y_{1}=1, x=1, y=2$ is the only solution to $3^{x}+1=2^{y}$ with $x \geq 1$. Now from $2-5^{g}=1$ we get $g=0$. This gives us $t=0$. Now this gives us the solution $1+3.16=49$ and $(t, x, y, z)=(0,1,2,7)$. This completes all the cases and thus the solutions are $(t, x, y, z)=(1,0,1,3),(0,1,0,2)$, $(2,2,2,13)$, and $(0,1,2,7)$. Note. The problem can be simplified by asking for solutions in positive integers (without significant loss in ideas). </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">(,x,y,z)=(1,0,1,3),(0,1,0,2),(2,2,2,13),(0,1,2,7)</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="57"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> NT5. Find all positive integers $n$ such that there exists a prime number $p$, such that $$ p^{n}-(p-1)^{n} $$ is a power of 3 . Note. A power of 3 is a number of the form $3^{a}$ where $a$ is a positive integer. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Suppose that the positive integer $n$ is such that $$ p^{n}-(p-1)^{n}=3^{a} $$ for some prime $p$ and positive integer $a$. If $p=2$, then $2^{n}-1=3^{a}$ by $(1)$, whence $(-1)^{n}-1 \equiv 0(\bmod 3)$, so $n$ should be even. Setting $n=2 s$ we obtain $\left(2^{s}-1\right)\left(2^{s}+1\right)=3^{a}$. It follows that $2^{s}-1$ and $2^{s}+1$ are both powers of 3 , but since they are both odd, they are co-prime, and we have $2^{s}-1=1$, i.e. $s=1$ and $n=2$. If $p=3$, then (1) gives $3 \mid 2^{n}$, which is impossible. Let $p \geq 5$. Then it follows from (1) that we can not have $3 \mid p-1$. This means that $2^{n}-1 \equiv 0$ $(\bmod 3)$, so $n$ should be even, and let $n=2 k$. Then $$ p^{2 k}-(p-1)^{2 k}=3^{a} \Longleftrightarrow\left(p^{k}-(p-1)^{k}\right)\left(p^{k}+(p-1)^{k}\right)=3^{a} $$ If $d=\left(p^{k}-(p-1)^{k}, p^{k}+(p-1)^{k}\right)$, then $d \mid 2 p^{k}$. However, both numbers are powers of 3 , so $d=1$ and $p^{k}-(p-1)^{k}=1, p^{k}+(p-1)^{k}=3^{a}$. If $k=1$, then $n=2$ and we can take $p=5$. For $k \geq 2$ we have $1=p^{k}-(p-1)^{k} \geq p^{2}-(p-1)^{2}$ (this inequality is equivalent to $p^{2}\left(p^{k-2}-1\right) \geq(p-1)^{2}\left((p-1)^{k-2}-1\right)$, which is obviously true). Then $1 \geq p^{2}-(p-1)^{2}=2 p-1 \geq 9$, which is absurd. It follows that the only solution is $n=2$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">2</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="58"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> A2. Let $a, b, c$ be positive real numbers such that abc $=1$. Show that $$ \frac{1}{a^{3}+b c}+\frac{1}{b^{3}+c a}+\frac{1}{c^{3}+a b} \leq \frac{(a b+b c+c a)^{2}}{6} $$ so </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. By the AM-GM inequality we have $a^{3}+b c \geq 2 \sqrt{a^{3} b c}=2 \sqrt{a^{2}(a b c)}=2 a$ and $$ \frac{1}{a^{3}+b c} \leq \frac{1}{2 a} $$ Similarly; $\frac{1}{b^{3}+c a} \leq \frac{1}{2 b} \cdot \frac{1}{c^{3}+a b} \leq \frac{1}{2 c}$ and then $$ \frac{1}{a^{3}+b c}+\frac{1}{b^{3}+c a}+\frac{1}{c^{3}+a b} \leq \frac{1}{2 a}+\frac{1}{2 b}+\frac{1}{2 c}=\frac{1}{2} \frac{a b+b c+c a}{a b c} \leq \frac{(a b+b c+c a)^{2}}{6} $$ Therefore it is enongil to prove $\frac{(a h+b c+c a)^{2}}{6} \leq \frac{(a b+b c+c a)^{2}}{6}$. This mequalits is trivially shomn to be equivalent to $3 \leq a b+b c+c a$ which is true because of the AM-GM inequalit: $3=\sqrt[3]{(a b c)^{2}} \leq a b+b c+c a$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="59"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> A3. Let $a . b$ c ce positue real numbers such that $a+b+c=a^{2}+b^{2}+c^{2}$. Shou that $$ \frac{a^{2}}{a^{2}+a b}+\frac{b^{2}}{b^{2}+b c}+\frac{c^{2}}{c^{2}+c a} \geq \frac{a+b+c}{2} $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. By the Cauchy-Schwarz inequality it is $$ \begin{aligned} & \left(\frac{a^{2}}{a^{2}+a b}+\frac{b^{2}}{b^{2}+b c}+\frac{c^{2}}{c^{2}+c a}\right)\left(\left(a^{2}+a b\right)+\left(b^{2}+b c\right)+\left(c^{2}+c a\right)\right) \geq(a+b+c)^{2} \\ \Rightarrow & \frac{a^{2}}{a^{2}+a b}+\frac{b^{2}}{b^{2}+b c}+\frac{c^{2}}{c^{2}+c a} \geq \frac{(a+b+c)^{2}}{a^{2}+b^{2}+c^{2}+a b+b c+c a} \end{aligned} $$ So in is enough to prove $\frac{(a+b+c)^{2}}{a^{2}+b^{2}+c^{2}+a b+b c+c a} \geq \frac{a+b+c}{2}$, that is to prove $$ 2(a+b+c) \geq a^{2}+b^{2}+c^{2}+a b+b c+c a $$ Substituting $a^{2}+b^{2}+c^{2}$ for $a+b+c$ into the left hand side we wish equivalently to prove $$ a^{2}+b^{2}+c^{2} \geq a b+b c+c a $$ But the $a^{2}+b^{2} \geq 2 a b, b^{2}+c^{2} \geq 2 b c, c^{2}+a^{2} \geq 2 c a$ which by addition imply the desired inequality. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="60"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> A4. Solve the following equation for $x, y, z \in \mathbb{N}$ $$ \left(1+\frac{x}{y+z}\right)^{2}+\left(1+\frac{y}{z+x}\right)^{2}+\left(1+\frac{z}{x+y}\right)^{2}=\frac{27}{4} $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution 1. Call $a=1+\frac{x}{y+z}, b=1+\frac{y}{z+x}, c=1+\frac{z}{x+y}$ to get $$ a^{2}+b^{2}+c^{2}=\frac{27}{4} $$ Since it is also true that $$ \frac{1}{a}+\frac{1}{b}+\frac{1}{c}=2 $$ the quadratic-harmonic means inequality implies $$ \frac{3}{2}=\sqrt{\frac{a^{2}+b^{2}+c^{2}}{3}} \geq \frac{3}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}=\frac{3}{2} $$ So the inequality in the middle holds as an equality, and this happens whenever $a=b=c$, from which $1+\frac{x}{y+z}=1+\frac{y}{z+x}=1+\frac{z}{x+y}$. But $1+\frac{x}{y+z}=1+\frac{y}{z+x} \Leftrightarrow x^{2}+x z=y^{2}+y z \Leftrightarrow(x-y)(x+y)=z(y-\dot{x})$ and the two sides of this equality will be of different sign, unless $x=y$ in which case both sides become 0 . So $x=y$, and similarly $y=z$, thus $x=y=z$. Indeed, any triad of equal natural numbers $x=y=z$ is a solution for the given equation, and so these are all its solutions. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">z</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Algebra</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="61"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> A5. Find the largest positive integer $n$ for which the inequality $$ \frac{a+b+c}{a b c+1}+\sqrt[n]{a b c} \leq \frac{5}{2} $$ holds for all $a, b, c \in[0,1]$. Here $\sqrt[1]{a b c}=a b c$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Let $n_{\max }$ be the sought largest value of $n$, and let $E_{a, b, c}(n)=\frac{a+b+c}{a b c+1}+\sqrt[n]{a b c}$. Then $E_{a, b, c}(m)-E_{a, b, c}(n)=\sqrt[m]{a b c}-\sqrt[n]{a b c}$ and since $a . b c \leq 1$ we clearly have $E_{a, b, c}(m) \geq$ $E_{a, b, c}(n)$ for $m \geq n$. So if $E_{a, b, c}(n) \geq \frac{5}{2}$ for some choice of $a, b, c \in[0,1]$, it must be $n_{\max } \leq n$. We use this remark to determine the upper bound $n_{\max } \leq 3$ by plugging some particular values of $a, b, c$ into the given inequality as follow's: $$ \text { For }(a, b, c)=(1,1, c), c \in[0,1] \text {, inequality (1) implies } \frac{c+2}{c+1}+\sqrt[n]{c} \leq \frac{5}{2} \Leftrightarrow \frac{1}{c+1}+\sqrt[n]{c} \leq $$ $\frac{3}{2}$. Obviously, every $x \in[0 ; 1]$ is written as $\sqrt[n]{c}$ for some $c \in[0 ; 1]$. So the last inequality is equivalent to: $$ \begin{aligned} & \frac{1}{x^{n}+1}+x \leq \frac{3}{2} \Leftrightarrow 2+2 x^{n+1}+2 x \leq 3 x^{n}+3 \Leftrightarrow 3 x^{n}+1 \geq 2 x^{n+1}+2 x \\ \Leftrightarrow & 2 x^{n}(1-x)+(1-x)+(x-1)\left(x^{n-1}+\cdots+x\right) \geq 0 \\ \Leftrightarrow & (1-x)\left[2 x^{n}+1-\left(x^{n-1}+x^{n-2}+\ldots+x\right)\right] \geq 0, \forall x \in[0,1] \end{aligned} $$ For $n=4$, the left hand side of the above becomes $(1-x)\left(2 x^{4}+1-x^{3}-x^{2}-x\right)=$ $(1-x)(x-1)\left(2 x^{3}+x^{2}-1\right)=-(1-x)^{2}\left(2 x^{3}+x^{2}-1\right)$ which for $x=0.9$ is negative. Thus. $n_{\max } \leq 3$ as claimed. Now, we shall prove that for $n=3$ inequality (1) holds for all $a, b, c \in[0,1]$, and this would mean $n_{\max }=3$. We shall use the following Lemma: Lemma. For all $a, b, c \in[0 ; 1]: a+b+c \leq a b c+2$. Proof of the Lemma: The required result comes by adding the following two inequalities side by side $$ \begin{aligned} & 0 \leq(a-1)(b-1) \Leftrightarrow a+b \leq a b+1 \Leftrightarrow a+b-a b \leq 1 \\ & 0 \leq(a b-1)(c-1) \Leftrightarrow a b+c \leq a b c+1 \end{aligned} $$ Because of the Lemma, our inequality (1) for $n=3$ wrill be proved if the following weaker inequality is proved for all $a, b, c \in[0,1]$ : $$ \frac{a b c+2}{a b c+1}+\sqrt[3]{a b c} \leq \frac{5}{2} \Leftrightarrow \frac{1}{a b c+1}+\sqrt[3]{a b c} \leq \frac{3}{2} $$ Denoting $\sqrt[3]{a b c}=y \in[0 ; 1]$, this inequality becomes: $$ \begin{aligned} & \frac{1}{y^{3}+1}+y \leq \frac{3}{2} \Leftrightarrow 2+2 y^{4}+2 y \leq 3 y^{3}+3 \Leftrightarrow-2 y^{4}+3 y^{3}-2 y+1 \geq 0 \\ \Leftrightarrow & 2 y^{3}(1-y)+(y-1) y(y+1)+(1-y) \geq 0 \Leftrightarrow(1-y)\left(2 y^{3}+1-y^{2}-y\right) \geq 0 \end{aligned} $$ The last inequality is obvious because $1-y \geq 0$ and $2 y^{3}+1-y^{2}-y=y^{3}+(y-1)^{2}(y+1) \geq 0$. ## Geometry 2 </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">3</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="62"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> G1. Let $A B C$ be an equilateral triangle, and $P$ a point on the circumcircle of the triangle $A B C$ and distinct from $A, B$ and $C$. If the lines through $P$ and parallel to $B C, C A, A B$ intersect the lines $C A, A B, B C$ at $M, N$ and $Q$ respectively, prove that $M, N$ and $Q$ are collinear. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Without any loss of generality, let $P$ be in the minor arc of the chord $A C$ as in Figure 1. Since $\angle P N A=\angle N P M=60^{\circ}$ and $\angle N A M=\angle P M A=120^{\circ}$, it follows that the points $A, M, P$ and $N$ are concyclic. This yields $$ \angle N M P=\angle N A P $$ ![](https://cdn.mathpix.com/cropped/2024_06_05_61d3145f18c90bf9f370g-05.jpg?height=663&width=551&top_left_y=933&top_left_x=795) Figure 1: Exercise G1. Similarly, since $\angle P M C=\angle M C Q=60^{\circ}$ and $\angle C Q P=60^{\circ}$, it follows that the points $P, M, Q$ and $C$ are concyclic. Thus $$ \angle P M Q=180^{\circ}-\angle P C Q=180^{\circ}-\angle N A P \stackrel{(2)}{=} 180^{\circ}-\angle N M P . $$ This implies $\angle P M Q+\angle N M P=180^{\circ}$, which shows that $M, N$ and $Q$ belong to the same line. 1 G2. Let $A B C$ be an isosceles triangle with $A B=A C$. Let also $c(K, K C)$ be a circle tangent to the line $A C$ at point $C$ which it intersects the segment $B C$ again at an interior point $H$. Prove that $H K \perp A B$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="63"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> G4. Let $A B C$ be an acute-angled triangle with circumcircle $\Gamma$, and let $O, H$ be the triangle's circumcenter and orthocenter respectively. Let also $A^{\prime}$ be the point where the angle bisector of angle $B A C$ meets $\Gamma$. If $A^{\prime} H=A H$, find the measure of angle $B A C$. ![](https://cdn.mathpix.com/cropped/2024_06_05_61d3145f18c90bf9f370g-07.jpg?height=519&width=1042&top_left_y=1756&top_left_x=541) Figure 4: Exercise G4. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. The segment $A A^{\prime}$ bisects $\angle O A H$ : if $\angle B C A=y$ (Figure 4), then $\angle B O A=$ $2 y$, and since $O A=O B$, it is $\angle O A B=\angle O B A=90^{\circ}-y$. Also since $A H \perp B C$, it is $\angle H A C=90^{\circ}-y=\angle O A B$ and the claim follows. Since $A . A^{\prime}$ bisects $\angle O A H$ and $A^{\prime} H=A H . O A^{\prime}=O A$, we have that the isosceles triangles $O A A^{\prime}, H A A^{\prime}$ are equal. Thus $$ A H=O A=R $$ where $R$ is the circumradius of triangle $A B C$. Call $\angle A C H=a$ and recall by the law of sines that $A H=2 R^{\prime} \sin a$, where $R^{\prime}$ is the circumradius of triangle $A H C$. Then (4) implies $$ R=2 R^{\prime} \sin a $$ But notice that $R=R^{\prime}$ because $\frac{A C}{\sin (A H C)}=2 R^{\prime}, \frac{A C}{\sin (A B C)}=2 R$ and $\sin (A H C)=$ $\sin \left(180^{\circ}-A B C\right)=\sin (A B C)$. So (5) gives $1=2 \sin a$, and $a$ as an acuite angle can only be $30^{\circ}$. Finally, $\angle B A C=90^{\circ}-a=60^{\circ}$. Remark. The steps in the above proof can be traced backwards making the converse also true, that is: If $\angle B A C=60^{\circ}$ then $A^{\prime} H=A H$. - G5. Let the circles $k_{1}$ and $k_{2}$ intersect at two distinct points $A$ and $B$, and let $t$ be a common tangent of $k_{1}$ and $k_{2}$ that touches them at $M$ and, $N$ respectively. If $t \perp A M$ and $M N=2 A M$, evaluate $\angle N M B$. ![](https://cdn.mathpix.com/cropped/2024_06_05_61d3145f18c90bf9f370g-08.jpg?height=540&width=1008&top_left_y=1454&top_left_x=589) Figure 5: Exercise G5. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">60</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="64"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> C1. Along a round table are arranged 11 cards with the names (all distinct) of the 11 members of the $16^{\text {th }}$ JBMO Problem Selection Committee. The distances between each two consecutive cards are equal. Assume that in the first meeting of the Committee none of its 11 members sits in front of the card with his name. Is it possible to rotate the table by some angle so that at the end at least two members of sit in front of the card with their names? </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Yes it is: Rotating the table by the angles $\frac{360^{\circ}}{11}, 2 \cdot \frac{360^{\circ}}{11}, 3 \cdot \frac{360^{\circ}}{11}, \ldots, 10 \cdot \frac{360^{\circ}}{11}$, we obtain 10 new positions of the table. By the assumption, it is obvious that every one of the 11 members of the Committee will be seated in front of the card with his name in exactly one of these 10 positions. Then by the Pigeonhole Principle there should exist one among these 10 positions in which at least two of the $11(>10)$ members of the Committee will be placed in their positions, as claimed. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="65"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> C2. $n$ nails nailed on a board are connected by two via a string. Each string is colored in one of $n$ given colors. For any three colors there exist three nails conne.cted by two with strings in these three colors. Can $n$ be: (a) 6, (b) 7? </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. (a) The answer is no: Suppose it is possible. Consider some color, say blue. Each blue string is the side of 4 triangles formed with vertices on the given points. As there exist $\binom{5}{2}=\frac{5 \cdot 4}{2}=10$ pairs of colors other than blue, and for any such pair of colors together with the blue color there exists a triangle with strings in these colors, we conclude that there exist at least 3 blue strings (otherwise the number of triangles with a blue string as a side would be at most $2 \cdot 4=8$, a contradiction). The same is true for any color, so altogether there exist at least $6 \cdot 3=18$ strings, while we have just $\binom{6}{2}=\frac{6 \cdot 5}{2}=15$ of them. ![](https://cdn.mathpix.com/cropped/2024_06_05_61d3145f18c90bf9f370g-12.jpg?height=519&width=488&top_left_y=1850&top_left_x=835) Figure 8: Exercise C2. (b) The answer is yes (Figure 8): Put the nails at the vertices of a regular 7-gon (Figure 8) and color each one of its sides in a different color. Now color each diagonal in the color of the unique side parallel to it. It can be checked directly that each triple of colors appears in some triangle (because of symmetry, it is enough to check only the triples containing the first color). Remark. The argument in (a) can be applied to any even $n$. The argument. in (b) can be applied to any odd $n=2 k+1$ as follows: first number the nails as $0,1,2 \ldots, 2 k$ and similarly number the colors as $0,1,2 \ldots, 2 k$. Then connect nail $x$ with nail $y$ by a string of color $x+y(\bmod n)$. For each triple of colors $(p, q, r)$ there are vertices $x, y, z$ connected by these three colors. Indeed, we need to solve (modn.) the system $$ (*)(x+y \equiv p, x+z \equiv q, y+z \equiv r) $$ Adding all three, we get $2(x+y+z) \equiv p+q+r$ and multiplying by $k+1$ we get $x+y+z \equiv$ $(k+1)(p+q+r)$. We can now find $x, y, z$ from the identities $(*)$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="66"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> C3. In a circle of diameter 1 consider 65 points no three of which are collinear. Prove that there exist 3 among these points which form a triangle with area less then or equal to $\frac{1}{72}$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Lemma: If a triangle $A B C$ lies in a rectangle $K L M N$. with sides $K L=a$ and $L M=b$, then the area of the triangle is less then or equal to $\frac{a b}{2}$. Proof of the lemma: Writhout any loss of generality assume that among the distance of $A, B, C$ from $K L$, that of $A$ is between the other two. Let $\ell$ be the line through $A$ and parallel to $K L$. Let $D$ be the intersection of $\ell, B C$ and $x, y$ the distances of $B, C$ from $\ell$ respectively. Then the area of $A B C$ equals $\frac{A D(x+y)}{2} \leq \frac{a b}{2}$, since $A D \leq a$ and $x+y \leq b$ and we are done. Now back to our problem, let us cover the circle with 24 squares of side $\frac{1}{6}$ and 8 other irregular and equal figures as shown in Figure 9, with boundary consisting of an arc on the circle and three line segments. Call $S=A D N M$ one of these figures. One of the line segments in the boundary of $S$ is of length $A D=A B-D B=\sqrt{A C^{2}-B C^{2}}-\frac{2}{6}=$ $\sqrt{\left(\frac{1}{2}\right)^{2}-\left(\frac{1}{6}\right)^{2}}-\frac{1}{3}=\frac{\sqrt{2}-1}{3}$. The boundary segment $M N$ goes through the center $C$ of the circle, forming with the horizontal lines an angle of $45^{\circ}$. The point in $S$ with maximum distance from the boundary segment $A B$ is the endpoint $M$ of the arc on the boundary of $S$. This distance equals $M E=M F-E F \stackrel{C M F=\text { isosceles }}{=} \frac{\sqrt{2}}{2} C M-\frac{1}{6}=\frac{\sqrt{2}}{4}-\frac{1}{6}=\frac{3 \sqrt{2}-2}{12}$. So $S$ can be put inside a rectangle $R$ with sides parallel to $A D, N D$ of lengths $\frac{\sqrt{2}-1}{3}$ and $\frac{3 \sqrt{2}-2}{12}$. So the triangle formed by any three points inside this figure, has an area less or equal to $\frac{1}{2} \cdot \frac{\sqrt{2}-1}{3} \cdot \frac{3 \sqrt{2}-2}{12}=\frac{8-5 \sqrt{2}}{72}<\frac{1}{72}$. Also, the triangle formed by any three points inside any square of side $\frac{1}{6}$, has an area less or equal to $\frac{1}{2} \cdot \frac{1}{6} \cdot \frac{1}{6}=\frac{1}{72}$. By the Pigeonhole Principle, we know that among the 65 given points there exist 3 inside the same one of the 32 squares and irregular figures of the picture covering the given circle. Then according to the above, the triangle formed by these 3 points has an area not exceeding $\frac{1}{72}$ as wanted. ![](https://cdn.mathpix.com/cropped/2024_06_05_61d3145f18c90bf9f370g-14.jpg?height=708&width=693&top_left_y=868&top_left_x=744) Figure 9: :Exercise C3. ## Number Theory 3 NT1. If $a, b$ are integers and $s=a^{3}+b^{3}-60 a b(a+b) \geq 2012$, find the least possible value of $s$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="67"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> NT5. Find all the positive integers $x, y, z, t$ such that $2^{x} \cdot 3^{y}+5^{z}=7^{t}$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Reducing modulo 3 we get $5^{z} \equiv 1$, therefore $z$ is even, $z=2 c, c \in \mathbb{N}$. . Next we prove that $t$ is even. Obviously, $t \geq 2$. Let us suppose that $t$ is odd, $t=2 d+1$, $d \in \mathbb{N}$. The equation becomes $2^{x} \cdot 3^{y}+25^{c}=7 \cdot 49^{d}$. If $x \geq 2$, reducing modulo 4 , we get $1 \equiv 3$, contradiction. For $x=1$, we have $2 \cdot 3^{y}+25^{c}=7 \cdot 49^{d}$; and, reducing modulo 24 , we obtain $2 \cdot 3^{y}+1 \equiv$ $7 \Rightarrow 24 \mid 2\left(3^{y}-3\right)$, i.e. $4 \mid 3^{y-1}-1$, which means that $y-1$ is even. Then, $y=2 b+1$, $b \in \mathbb{N}$. We obtain $6 \cdot 9^{b}+25^{c}=7 \cdot 49^{d}$, and, reducing modulo 5 , we get $(-1)^{b} \equiv 2 \cdot(-1)^{d}$, which is false, for all $b, d \in \mathbb{N}$. Hence $t$ is even, $t=2 d, d \in \mathbb{N}$. . The equation can be written as $2^{x} \cdot 3^{y}+25^{c}=49^{d} \Leftrightarrow 2^{x} \cdot 3^{y}=\left(7^{d}-5^{c}\right)\left(7^{d}+5^{c}\right) . \quad$. As $\operatorname{gcd}\left(7^{d}-5^{c}, 7^{d}+5^{c}\right)=2$ and $7^{c}+5^{c}>2$, there exist exactly three possibilities:(1) $\left\{\begin{array}{l}7^{d}-5^{c}=2^{x-1} \\ 7^{d}+5^{c}=2 \cdot 3^{y}\end{array}\right.$ (2) $\left\{\begin{array}{l}7^{d}-5^{c}=2 \cdot 3^{y} \\ 7^{d}+5^{c}=2^{x-1}\end{array}\right.$ (3) $\left\{\begin{array}{l}7^{d}-5^{c}=2 \\ 7^{d}+5^{c}=2^{x-1} \cdot 3^{y}\end{array}\right.$ Case (1). We have $7^{d}=2^{x-2}+3^{y}$ and, reducing modulo 3 , we get $2^{x-2} \equiv 1(\bmod 3)$, hence $x-2$ is even, i.e. $x=2 a+2$, where $a \in \mathbb{N}$, since $a=0$ would mean $3^{y}+1=7^{d}$, which is impossible (even $=$ odd). We obtain $7^{d}-5^{c}=2 \cdot 4^{a} \stackrel{\text { mod } 4}{\Longrightarrow} 7^{d} \equiv 1(\bmod 4) \Rightarrow d=2 e, e \in \mathbb{N}$. Then $49^{e}-5^{c}=$ $2 \cdot 4^{k} \stackrel{\bmod 8}{\Longrightarrow} 5^{c} \equiv 1(\bmod 8) \Rightarrow c=2 f, f \in \mathbb{N}$. We obtain $49^{e}-25^{f}=2: 4^{a} \xlongequal{\bmod 3} 0 \equiv 2(\bmod 3)$, false. In conclusion, in this case there are no solutions to the equation. Case (2). From $2^{x-1}=7^{d}+5^{c} \geq 12$, we obtain $x \geq 5$. Then $7^{d}+5^{c} \equiv 0(\bmod .4)$, i.e. $3^{d}+1 \equiv 0(\bmod 4)$, hence $d$ is odd. As $7^{d}=5^{c}+2 \cdot 3^{y} \geq 11$, we get $d \geq 2$, hence $d=2 e+1$, $e \in \mathbb{N}$. As in the previous case, from $7^{d}=2^{x-2}+3^{y}$, reducing modulo 3, we obtain $x=2 a+2$, with $a \geq 2$ (because $x \geq 5$ ). We get $7^{d}=4^{a}+3^{y}$, i.e. $7 \cdot 49^{e}=4^{a}+3^{y}$, hence, reducing modulo 8 , we obtain $7 \equiv 3^{y}$, which is false, because $3^{y}$ is congruent mod8 either to 1 (if $y$ is even) or to. 3 (if $y$ is odd). In conclusion, in this case there are no solutions to the equation. $k \in \mathbb{N}$. Case (3). From $7^{d}=5^{c}+2$, it follows that the last digit of $7^{d}$ is 7 , hence $d=4 k+1$, false. If $c \geq 2$, from $7^{4 k+1}=5^{c}+2$, reducing modulo 25 , we obtain $7 \equiv 2(\bmod 25)$, which is For $c=1$ we get $d=1$, and the solution $x=3, y=1, z=t=2$. 3 NT6. If $a, b, c, d$ are integers and $A=2(a-2 b+c)^{4}+2(b-2 c+a)^{4}+2(c-2 a+b)^{4}$, $B=d(d+1)(d+2)(d+3)+1$, prove that $(\sqrt{A}+1)^{2}+B$ cannot be a perfect square. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">3,1,=2</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="68"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> A1. Find all ordered triples $(x, y, z)$ of real numbers satisfying the following system of equations: $$ \begin{aligned} x^{3} & =\frac{z}{y}-2 \frac{y}{z} \\ y^{3} & =\frac{x}{z}-2 \frac{z}{x} \\ z^{3} & =\frac{y}{x}-2 \frac{x}{y} \end{aligned} $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. We have $$ \begin{aligned} & x^{3} y z=z^{2}-2 y^{2} \\ & y^{3} z x=x^{2}-2 z^{2} \\ & z^{3} x y=y^{2}-2 x^{2} \end{aligned} $$ with $x y z \neq 0$. Adding these up we obtain $\left(x^{2}+y^{2}+z^{2}\right)(x y z+1)=0$. Hence $x y z=-1$. Now the system of equations becomes: $$ \begin{aligned} & x^{2}=2 y^{2}-z^{2} \\ & y^{2}=2 z^{2}-x^{2} \\ & z^{2}=2 x^{2}-y^{2} \end{aligned} $$ Then the first two equations give $x^{2}=y^{2}=z^{2}$. As $x y z=-1$, we conclude that $(x, y, z)=$ $(1,1,-1),(1,-1,1),(-1,1,1)$ and $(-1,-1,-1)$ are the only solutions. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">(1,1,-1),(1,-1,1),(-1,1,1),(-1,-1,-1)</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Algebra</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="69"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> A2. Find the largest possible value of the expression $\left|\sqrt{x^{2}+4 x+8}-\sqrt{x^{2}+8 x+17}\right|$ where $x$ is a real number. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. We observe that $$ \left|\sqrt{x^{2}+4 x+8}-\sqrt{x^{2}+8 x+17}\right|=\left|\sqrt{(x-(-2))^{2}+(0-2)^{2}}-\sqrt{\left.(x-(-4))^{2}+(0-1)^{2}\right)}\right| $$ is the absolute difference of the distances from the point $P(x, 0)$ in the $x y$-plane to the points $A(-2,2)$ and $B(-4,1)$. By the Triangle Inequality, $|P A-P B| \leq|A B|$ and the equality occurs exactly when $P$ lies on the line passing through $A$ and $B$, but not between them. If $P, A, B$ are collinear, then $(x-(-2)) /(0-2)=((-4)-(-2)) /(1-2)$. This gives $x=-6$, and as $-6<-4<-2$, $$ \left|\sqrt{(-6)^{2}+4(-6)+8}-\sqrt{(-6)^{2}+8(-6)+17}\right|=|\sqrt{20}-\sqrt{5}|=\sqrt{5} $$ is the largest possible value of the expression. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">\sqrt{5}</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Algebra</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="70"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> A3. Show that $$ \left(a+2 b+\frac{2}{a+1}\right)\left(b+2 a+\frac{2}{b+1}\right) \geq 16 $$ for all positive real numbers $a, b$ satisfying $a b \geq 1$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution 1. By the AM-GM Inequality we have: $$ \frac{a+1}{2}+\frac{2}{a+1} \geq 2 $$ Therefore $$ a+2 b+\frac{2}{a+1} \geq \frac{a+3}{2}+2 b $$ and, similarly, $$ b+2 a+\frac{2}{b+1} \geq 2 a+\frac{b+3}{2} $$ On the other hand, $$ (a+4 b+3)(b+4 a+3) \geq(\sqrt{a b}+4 \sqrt{a b}+3)^{2} \geq 64 $$ by the Cauchy-Schwarz Inequality as $a b \geq 1$, and we are done. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="71"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> C3. All possible pairs of $n$ apples are weighed and the results are given to us in an arbitrary order. Can we determine the weights of the apples if a. $n=4$, b. $n=5$, c. $n=6$ ? </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. a. No. Four apples with weights $1,5,7,9$ and with weights $2,4,6,10$ both give the results $6,8,10,12,14,16$ when weighed in pairs. b. Yes. Let $a \leq b \leq c \leq d \leq e$ be the weights of the apples. As each apple is weighed 4 times, by adding all 10 pairwise weights and dividing the sum by 4 , we obtain $a+b+c+d+e$. Subtracting the smallest and the largest pairwise weights $a+b$ and $d+e$ from this we obtain c. Subtracting $c$ from the second largest pairwise weight $c+e$ we obtain $e$. Subtracting $e$ from the largest pairwise weight $d+e$ we obtain $d$. $a$ and $b$ are similarly determined. c. Yes. Let $a \leq b \leq c \leq d \leq e \leq f$ be the weights of the apples. As each apple is weighed 5 times, by adding all 15 pairwise weights and dividing the sum by 5 , we obtain $a+b+c+d+e+f$. Subtracting the smallest and the largest pairwise weights $a+b$ and $e+f$ from this we obtain $c+d$. Subtracting the smallest and the second largest pairwise weights $a+b$ and $d+f$ from $a+b+c+d+e+f$ we obtain $c+e$. Similarly we obtain $b+d$. We use these to obtain $a+f$ and $b+e$. Now $a+d, a+e, b+c$ are the three smallest among the remaining six pairwise weights. If we add these up, subtract the known weights $c+d$ and $b+e$ form the sum and divide the difference by 2 , we obtain $a$. Then the rest follows. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Combinatorics</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="72"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> G1. Let $A B$ be a diameter of a circle $\omega$ with center $O$ and $O C$ be a radius of $\omega$ which is perpendicular to $A B$. Let $M$ be a point on the line segment $O C$. Let $N$ be the second point of intersection of the line $A M$ with $\omega$, and let $P$ be the point of intersection of the lines tangent to $\omega$ at $N$ and at $B$. Show that the points $M, O, P, N$ are concyclic. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Since the lines $P N$ and $B P$ are tangent to $\omega, N P=P B$ and $O P$ is the bisector of $\angle N O B$. Therefore the lines $O P$ and $N B$ are perpendicular. Since $\angle A N B=90^{\circ}$, it follows that the lines $A N$ and $O P$ are parallel. As $M O$ and $P B$ are also parallel and $A O=O B$, the triangles $A M O$ and $O P B$ are congruent and $M O=P B$. Hence $M O=N P$. Therefore $M O P N$ is an isosceles trapezoid and therefore cyclic. Hence the points $M, O, P, N$ are concyclic. ![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-16.jpg?height=1267&width=1249&top_left_y=779&top_left_x=382) 8.2. $\omega_{1}$ and $\omega_{2}$ are two circles that are externally tangent to each other at the point $M$ and internally tangent to a circle $\omega_{3}$ at the points $K$ and $L$, respectively. Let $A$ and $B$ be the two points where the common tangent line at $M$ to $\omega_{1}$ and $\omega_{2}$ intersects $\omega_{3}$. Show that if $\angle K A B=\angle L A B$ then the line segment $A B$ is a diameter of $\omega_{3}$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="73"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> G3. Let $D$ be a point on the side $B C$ of an acute triangle $A B C$ such that $\angle B A D=\angle C A O$ where $O$ is the center of the circumcircle $\omega$ of the triangle $A B C$. Let $E$ be the second point of intersection of $\omega$ and the line $A D$. Let $M, N, P$ be the midpoints of the line segments $B E, O D, A C$, respectively. Show that $M, N, P$ are collinear. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. We will show that $M O P D$ is a parallelogram. From this it follows that $M, N$, $P$ are collinear. Since $\angle B A D=\angle C A O=90^{\circ}-\angle A B C, D$ is the foot of the perpendicular from $A$ to side $B C$. Since $M$ is the midpoint of the line segment $B E$, we have $B M=M E=M D$ and hence $\angle M D E=\angle M E D=\angle A C B$. Let the line $M D$ intersect the line $A C$ at $D_{1}$. Since $\angle A D D_{1}=\angle M D E=\angle A C D, M D$ is perpendicular to $A C$. On the other hand, since $O$ is the center of the circumcircle of triangle $A B C$ and $P$ is the midpoint of the side $A C, O P$ is perpendicular to $A C$. Therefore $M D$ and $O P$ are parallel. Similarly, since $P$ is the midpoint of the side $A C$, we have $A P=P C=D P$ and hence $\angle P D C=\angle A C B$. Let the line $P D$ intersect the line $B E$ at $D_{2}$. Since $\angle B D D_{2}=\angle P D C=$ $\angle A C B=\angle B E D$, we conclude that $P D$ is perpendicular to $B E$. Since $M$ is the midpoint of the line segment $B E, O M$ is perpendicular to $B E$ and hence $O M$ and $P D$ are parallel. ![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-18.jpg?height=1238&width=1335&top_left_y=1217&top_left_x=359) </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="74"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> G4. Let $I$ be the incenter and $A B$ the shortest side of a triangle $A B C$. The circle with center $I$ and passing through $C$ intersects the ray $A B$ at the point $P$ and the ray $B A$ at the point $Q$. Let $D$ be the point where the excircle of the triangle $A B C$ belonging to angle $A$ touches the side $B C$, and let $E$ be the symmetric of the point $C$ with respect to $D$. Show that the lines $P E$ and $C Q$ are perpendicular. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. First we will show that points $P$ and $Q$ are not on the line segment $A B$. Assume that $Q$ is on the line segment $A B$. Since $C I=Q I$ and $\angle I B Q=\angle I B C$, either the triangles $C B I$ and $Q B I$ are congruent or $\angle I C B+\angle I Q B=180^{\circ}$. In the first case, we have $B C=B Q$ which contradicts $A B$ being the shortest side. In the second case, we have $\angle I Q A=\angle I C B=\angle I C A$ and the triangles $I A C$ and $I A Q$ are congruent. Hence this time we have $A C=A Q$, contradicting $A B$ being the shortest side. ![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-19.jpg?height=677&width=1058&top_left_y=874&top_left_x=520) Case 1 ![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-19.jpg?height=686&width=1058&top_left_y=1733&top_left_x=498) Now we will show that the lines $P E$ and $C Q$ are perpendicular. Since $\angle I Q B \leq \angle I A B=(\angle C A B) / 2<90^{\circ}$ and $\angle I C B=(\angle A C B) / 2<90^{\circ}$, the triangles $C B I$ and $Q B I$ are congruent. Hence $B C=B Q$ and $\angle C Q P=\angle C Q B=90^{\circ}-(\angle A B C) / 2$. Similarly, we have $A C=A P$ and hence $B P=A C-A B$. On the other hand, as $D E=C D$ and $C D+A C=u$, where $u$ denotes the semiperimeter of the triangle $A B C$, we have $B E=B C-2(u-A C)=A C-A B$. Therefore $B P=B E$ and $\angle Q P E=(\angle A B C) / 2$. Hence, $\angle C Q P+\angle Q P E=90^{\circ}$. ![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-20.jpg?height=1393&width=1427&top_left_y=773&top_left_x=333) </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="75"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> G5. A circle passing through the midpoint $M$ of the side $B C$ and the vertex $A$ of a triangle $A B C$ intersects the sides $A B$ and $A C$ for the second time at the points $P$ and $Q$, respectively. Show that if $\angle B A C=60^{\circ}$ then $$ A P+A Q+P Q<A B+A C+\frac{1}{2} B C $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. Since the quadrilateral $A P M Q$ is cyclic, we have $\angle P M Q=180^{\circ}-\angle P A Q=$ $180^{\circ}-\angle B A C=120^{\circ}$. Therefore $\angle P M B+\angle Q M C=180^{\circ}-\angle P M Q=60^{\circ}$. Let the point $B^{\prime}$ be the symmetric of the point $B$ with respect to the line $P M$ and the point $C^{\prime}$ be the symmetric of the point $C$ with respect to the line $Q M$. The triangles $B^{\prime} M P$ and $B M P$ are congruent and the triangles $C^{\prime} M Q$ and $C M Q$ are congruent. Hence $\angle B^{\prime} M C^{\prime}=\angle P M Q-\angle B^{\prime} M P-\angle C^{\prime} M Q=120^{\circ}-\angle B M P-\angle C M Q=120^{\circ}-60^{\circ}=60^{\circ}$. As we also have $B^{\prime} M=B M=C M=C^{\prime} M$, we conclude that the triangle $B^{\prime} M C^{\prime}$ is equilateral and $B^{\prime} C^{\prime}=B C / 2$. ![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-21.jpg?height=898&width=1153&top_left_y=978&top_left_x=493) On the other hand, we have $P B^{\prime}+B^{\prime} C^{\prime}+C^{\prime} Q \geq P Q$ by the Triangle Inequality, and hence $P B+B C / 2+Q C \geq P Q$. This gives the inequality $A B+B C / 2+A C \geq A P+P Q+A Q$. We get an equality only when the points $B^{\prime}$ and $C^{\prime}$ lie on the line segment $P Q$. If this is the case, then $\angle P Q C+\angle Q P B=2(\angle P Q M+\angle Q P M)=120^{\circ}$ and therefore $\angle A P Q+\angle A Q P=$ $240^{\circ} \neq 120^{\circ}$, a contradiction. $A B C D$. Let $K$ and $M$ be the points of intersection of the line $P D$ with $Q B$ and $Q A$, respectively, and let $N$ be the point of intersection of the lines $P A$ and $Q B$. Let $X, Y, Z$ be the midpoints of the line segments $A N, K N, A M$, respectively. Let $\ell_{1}$ be the line passing through $X$ and perpendicular to $M K, \ell_{2}$ be the line passing through $Y$ and perpendicular to $A M, \ell_{3}$ be the line passing through $Z$ and perpendicular to $K N$. Show that $\ell_{1}, \ell_{2}, \ell_{3}$ are concurrent. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="76"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> N1. Find all positive integere on for othich $1^{2}+2^{2}+\cdots+16^{2}+17$ is a perfort square </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. We bave $1^{3}+2^{5}+\cdots+16^{2}=(1+2+\cdots+16)^{2}=5^{2} \quad 17^{0}$ Herese. $11^{3}+2^{3}+$ ![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-24.jpg?height=83&width=1607&top_left_y=309&top_left_x=263) meeger t then $1 T^{\prime}-(1+B)(t-3)$ A. $(1,5) \quad(t-3)=16$ this can coly happen ![](https://cdn.mathpix.com/cropped/2024_06_05_66b0df6ec561017d2840g-24.jpg?height=74&width=1467&top_left_y=415&top_left_x=206) Eirornd all ordered triples $(x, y, z)$ of integers satisfying $20^{x}+13^{y}=2013^{z}$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"></div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Incomplete</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Incomplete</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="77"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> N3. Find all ordered pairs $(a, b)$ of positive integers for which the numbers $\frac{a^{3} b-1}{a+1}$ and $\frac{b^{3} a+1}{b-1}$ are positive integers. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. As $a^{3} b-1=b\left(a^{3}+1\right)-(b+1)$ and $a+1 \mid a^{3}+1$, we have $a+1 \mid b+1$. As $b^{3} a+1=a\left(b^{3}-1\right)+(a+1)$ and $b-1 \mid b^{3}-1$, we have $b-1 \mid a+1$. So $b-1 \mid b+1$ and hence $b-1 \mid 2$. - If $b=2$, then $a+1 \mid b+1=3$ gives $a=2$. Hence $(a, b)=(2,2)$ is the only solution in this case. - If $b=3$, then $a+1 \mid b+1=4$ gives $a=1$ or $a=3$. Hence $(a, b)=(1,3)$ and $(3,3)$ are the only solutions in this case. To summarize, $(a, b)=(1,3),(2,2)$ and $(3,3)$ are the only solutions. $\mathbf{N 4}$. A rectangle in the $x y$-plane is called latticed if all its vertices have integer coordinates. a. Find a latticed rectangle with area 2013 whose sides are not parallel to the axes. b. Show that if a latticed rectangle has area 2011, then its sides are parallel to the axes. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">(1,3),(2,2),(3,3)</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="78"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> N5. Find all ordered triples $(x, y, z)$ of positive integers satisfying the equation $$ \frac{1}{x^{2}}+\frac{y}{x z}+\frac{1}{z^{2}}=\frac{1}{2013} $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. We have $x^{2} z^{2}=2013\left(x^{2}+x y z+z^{2}\right)$. Let $d=\operatorname{gcd}(x, z)$ and $x=d a, z=d b$. Then $a^{2} b^{2} d^{2}=2013\left(a^{2}+a b y+b^{2}\right)$. As $\operatorname{gcd}(a, b)=1$, we also have $\operatorname{gcd}\left(a^{2}, a^{2}+a b y+b^{2}\right)=1$ and $\operatorname{gcd}\left(b^{2}, a^{2}+a b y+b^{2}\right)=1$. Therefore $a^{2} \mid 2013$ and $b^{2} \mid 2013$. But $2013=3 \cdot 11 \cdot 61$ is squarefree and therefore $a=1=b$. Now we have $x=z=d$ and $d^{2}=2013(y+2)$. Once again as 2013 is squarefree, we must have $y+2=2013 n^{2}$ where $n$ is a positive integer. Hence $(x, y, z)=\left(2013 n, 2013 n^{2}-2,2013 n\right)$ where $n$ is a positive integer. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">(x,y,z)=(2013n,2013n^{2}-2,2013n)</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="79"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> N6. Find all ordered triples $(x, y, z)$ of integers satisfying the following system of equations: $$ \begin{aligned} x^{2}-y^{2} & =z \\ 3 x y+(x-y) z & =z^{2} \end{aligned} $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution. If $z=0$, then $x=0$ and $y=0$, and $(x, y, z)=(0,0,0)$. Let us assume that $z \neq 0$, and $x+y=a$ and $x-y=b$ where $a$ and $b$ are nonzero integers such that $z=a b$. Then $x=(a+b) / 2$ and $y=(a-b) / 2$, and the second equations gives $3 a^{2}-3 b^{2}+4 a b^{2}=4 a^{2} b^{2}$. Hence $$ b^{2}=\frac{3 a^{2}}{4 a^{2}-4 a+3} $$ and $$ 3 a^{2} \geq 4 a^{2}-4 a+3 $$ which is satisfied only if $a=1,2$ or 3 . - If $a=1$, then $b^{2}=1 .(x, y, z)=(1,0,1)$ and $(0,1,-1)$ are the only solutions in this case. - If $a=2$, then $b^{2}=12 / 11$. There are no solutions in this case - If $a=3$, then $b^{2}=1 .(x, y, z)=(1,2,-3)$ and $(2,1,3)$ are the only solutions in this case. To summarize, $(x, y, z)=(0,0,0),(1,0,1),(0,1,-1),(1,2,-3)$ and $(2,1,3)$ are the only solutions. Comments. 1. The original problem proposal asks for the solutions when $z=p$ is a prime number. 2. The problem can be asked with a single equation in the form: $$ 3 x y+(x-y)^{2}(x+y)=\left(x^{2}-y^{2}\right)^{2} $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">(0,0,0),(1,0,1),(0,1,-1),(1,2,-3),(2,1,3)</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Algebra</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="80"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## A1 MLD Let $x, y, z$ be real numbers, satisfying the relations $$ \left\{\begin{array}{l} x \geq 20 \\ y \geq 40 \\ z \geq 1675 \\ x+y+z=2015 \end{array}\right. $$ Find the greatest value of the product $P=x \cdot y \cdot z$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution 1: By virtue of $z \geq 1675$ we have $$ y+z<2015 \Leftrightarrow y<2015-z \leq 2015-1675<1675 $$ It follows that $(1675-y) \cdot(1675-z) \leq 0 \Leftrightarrow y \cdot z \leq 1675 \cdot(y+z-1675)$. By using the inequality $u \cdot v \leq\left(\frac{u+v}{2}\right)^{2}$ for all real numbers $u, v$ we obtain $$ \begin{gathered} P=x \cdot y \cdot z \leq 1675 \cdot x \cdot(y+z-1675) \leq 1675 \cdot\left(\frac{x+y+z-1675}{2}\right)^{2}= \\ 1675 \cdot\left(\frac{2015-1675}{2}\right)^{2}=1675 \cdot 170^{2}=48407500 \end{gathered} $$ $$ \text { We have } P=x \cdot y \cdot z=48407500 \Leftrightarrow\left\{\begin{array} { l } { x + y + z = 2 0 1 5 , } \\ { z = 1 6 7 5 , } \\ { x = y + z - 1 6 7 5 } \end{array} \Leftrightarrow \left\{\begin{array}{l} x=170 \\ y=170 \\ z=1675 \end{array}\right.\right. $$ So, the greatest value of the product is $P=x \cdot y \cdot z=48407500$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">48407500</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Algebra</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="81"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## A2 ALB 3) If $x^{3}-3 \sqrt{3} x^{2}+9 x-3 \sqrt{3}-64=0$, find the value of $x^{6}-8 x^{5}+13 x^{4}-5 x^{3}+49 x^{2}-137 x+2015$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> Solution $x^{3}-3 \sqrt{3} x^{2}+9 x-3 \sqrt{3}-64=0 \Leftrightarrow(x-\sqrt{3})^{3}=64 \Leftrightarrow(x-\sqrt{3})=4 \Leftrightarrow x-4=\sqrt{3} \Leftrightarrow x^{2}-8 x+16=3 \Leftrightarrow$ $x^{2}-8 x+13=0$ $x^{6}-8 x^{5}+13 x^{4}-5 x^{3}+49 x^{2}-137 x+2015=\left(x^{2}-8 x+13\right)\left(x^{4}-5 x+9\right)+1898=0+1898=1898$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">1898</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Algebra</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="82"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## A3 MNE Let $a, b, c$ be positive real numbers. Prove that $$ \frac{a}{b}+\sqrt{\frac{b}{c}}+\sqrt[3]{\frac{c}{a}}>2 $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution: Starting from the double expression on the left-hand side of given inequality, and applying twice the Arithmetic-Geometric mean inequality, we find that $$ \begin{aligned} 2 \frac{a}{b}+2 \sqrt{\frac{b}{c}}+2 \sqrt[3]{\frac{c}{a}} & =\frac{a}{b}+\left(\frac{a}{b}+\sqrt{\frac{b}{c}}+\sqrt{\frac{b}{c}}\right)+2 \sqrt[3]{\frac{c}{a}} \\ & \geq \frac{a}{b}+3 \sqrt[3]{\frac{a}{b}} \sqrt{\frac{b}{c}} \sqrt{\frac{b}{c}}+2 \sqrt[3]{\frac{c}{a}} \\ & =\frac{a}{b}+3 \sqrt[3]{\frac{a}{c}}+2 \sqrt[3]{\frac{c}{a}} \\ & \left.=\frac{a}{b}+\sqrt[3]{\frac{a}{c}}+2 \sqrt[3]{\frac{a}{c}}+\sqrt[3]{\frac{c}{a}}\right) \\ & \geq \frac{a}{b}+\sqrt[3]{\frac{a}{c}}+2 \cdot 2 \sqrt{\sqrt[3]{\frac{a}{c}} \sqrt[3]{\frac{c}{a}}} \\ & =\frac{a}{b}+\sqrt[3]{\frac{a}{c}}+4 \\ & >4 \end{aligned} $$ which yields the given inequality. (A4) GRE Let $a, b, c$ be positive real numbers such that $a+b+c=3$. Find the minimum value of $$ A=\frac{2-a^{3}}{a}+\frac{2-b^{3}}{b}+\frac{2-c^{3}}{c} $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">4</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="83"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## A5 MKCD Let $x, y, z$ be positive real numbers that satisfy the equality $x^{2}+y^{2}+z^{2}=3$. Prove that $$ \frac{x^{2}+y z}{x^{2}+y z+1}+\frac{y^{2}+z x}{y^{2}+z x+1}+\frac{z^{2}+x y}{z^{2}+x y+1} \leq 2 $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution: We have $$ \begin{aligned} & \frac{x^{2}+y z}{x^{2}+y z+1}+\frac{y^{2}+z x}{y^{2}+z x+1}+\frac{z^{2}+x y}{z^{2}+x y+1} \leq 2 \Leftrightarrow \\ & \frac{x^{2}+y z+1}{x^{2}+y z+1}+\frac{y^{2}+z x+1}{y^{2}+z x+1}+\frac{z^{2}+x y+1}{z^{2}+x y+1} \leq 2+\frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \Leftrightarrow \\ & 3 \leq 2+\frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \Leftrightarrow \\ & 1 \leq \frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \\ & \frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \geq \frac{9}{x^{2}+y z+1+y^{2}+z x+1+z^{2}+x y+1}= \\ & \frac{9}{x^{2}+y^{2}+z^{2}+x y+y z+z x+3} \geq \frac{9}{2 x^{2}+y^{2}+z^{2}+3}=1 \end{aligned} $$ The first inequality: AM-GM inequality (also can be achieved with Cauchy-BunjakowskiSchwarz inequality). The second inequality: $x y+y z+z x £ x^{2}+y^{2}+z^{2}$ (there are more ways to prove it, AM-GM, full squares etc.) ## GEOMETRY </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Inequalities</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="84"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## G1 MNE Around the triangle $A B C$ the circle is circumscribed, and at the vertex $C$ tangent $t$ to this circle is drawn. The line $p$ which is parallel to this tangent intersects the lines $B C$ and $A C$ at the points $D$ and $E$, respectively. Prove that the points $A, B, D, E$ belong to the same circle. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution: Let $O$ be the center of a circumscribed circle $k$ of the triangle $A B C$, and let $F$ and $G$ be the points of intersection of the line $C O$ with the line $p$ and the circle $k$, respectively (see Figure). From $p \| t$ it follows that $p \perp C O$. Furthermore, $\angle A B C=\angle A G C$, because these angles are peripheral over the same chord. The quadrilateral $A G F E$ has two right angles at the vertices $A$ and $F$, and hence, $\angle A E D+\angle A B D=\angle A E F+\angle A G F=180^{\circ}$. Hence, the quadrilateral $A B D E$ is cyclic, as asserted. ![](https://cdn.mathpix.com/cropped/2024_06_05_07a1b610f48bd7c35addg-06.jpg?height=406&width=483&top_left_y=2006&top_left_x=843) Figure </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="85"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## G2 MLD The point $P$ is outside of the circle $\Omega$. Two tangent lines, passing from the point $P$, touch the circle $\Omega$ at the points $A$ and $B$. The median $A M, M \in(B P)$, intersects the circle $\Omega$ at the point $C$ and the line $P C$ intersects again the circle $\Omega$ at the point $D$. Prove that the lines $A D$ and $B P$ are parallel. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution: Since $\angle B A C=\angle B A M=\angle M B C$, we have $\triangle M A B \cong \triangle M B C$. ![](https://cdn.mathpix.com/cropped/2024_06_05_07a1b610f48bd7c35addg-07.jpg?height=498&width=745&top_left_y=735&top_left_x=625) We obtain $\frac{M A}{M B}=\frac{M B}{M C}=\frac{A B}{B C}$. The equality $\quad M B=M P$ implies $\frac{M A}{M P}=\frac{M P}{M C}$ and $\angle P M C \equiv \angle P M A$ gives the relation $\triangle P M A \cong \triangle C M P$. It follows that $\angle B P D \equiv \angle M P C \equiv \angle M A P \equiv \angle C A P \equiv \angle C D A \equiv \angle P D A$. So, the lines $A D$ and $B P$ are parallel. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="86"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## G3 GRE Let $c \equiv c(O, K)$ be a circle with center $O$ and radius $R$ and $A, B$ be two points on it, not belonging to the same diameter. The bisector of the angle $A \hat{B} O$ intersects the circle $c$ at point $C$, the circumcircle of the triangle $A O B$, say ${ }^{c_{1}}$ at point $K$ and the circumcircle of the triangle $A O C$, say ${ }^{c_{2}}$, at point $L$. Prove that the point $K$ is the circumcenter of the triangle $A O C$ and the point $L$ is the incenter of the triangle $A O B$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution: The segments $O B, O C$ are equal, as radii of the circle ${ }^{c}$. Hence $O B C$ is an isosceles triangle and $$ \hat{B}_{1}=\hat{C}_{1}=\hat{x} $$ ![](https://cdn.mathpix.com/cropped/2024_06_05_07a1b610f48bd7c35addg-07.jpg?height=414&width=545&top_left_y=2097&top_left_x=714) The chord $B C$ is the bisector of the angle $O \hat{B} A$, and hence $$ \hat{B}_{1}=\hat{B}_{2}=\hat{x} $$ The angles $\hat{B}_{2}$ and $\hat{O}_{1}$ are inscribed to the same arc $O K$ of the circle ${ }^{c_{1}}$ and hence $$ \hat{B}_{2}=\hat{\mathrm{O}}_{1}=\hat{x} $$ The segments $K O, K C$ are equal, as radii of the circle ${ }^{c_{2}}$. Hence the triangle $K O C$ is isosceles and so $$ \hat{O}_{2}=\hat{C}_{1}=\hat{x} $$ From equalities $(1),(2),(3)$ we conclude that $$ \hat{O}_{1}=\hat{O}_{2}=\hat{x} $$ and so $O K$ is the bisector, and hence perpendicular bisector of the isosceles triangle $O A C$. The point $K$ is the middle of the arc $O K$ (since $B K$ bisects the angle $O \hat{B} A$ ). Hence the perpendicular bisector of the chord $A O$ of the circle ${ }^{c_{1}}$ is passing through point $K$. It means that $K$ is the circumcenter of the triangle $O A C$. From equalities (1),(2),(3) we conclude that $\hat{B}_{2}=\hat{C}_{1}=\hat{x}$ and so $A B / / O C \Rightarrow O \hat{A} B=A \hat{O} C$, that is $\hat{A}_{1}+\hat{A}_{2}=\hat{O}_{1}+\hat{O}_{2}$ and since $\hat{O}_{1}=\hat{O}_{2}=\hat{x}$, we conclude that $$ \hat{A}_{1}+\hat{A}_{2}=2 \hat{O}_{1}=2 \hat{x} $$ The angles $\hat{A}_{I}$ and $\hat{C}_{I}$ are inscribed into the circle ${ }^{c_{2}}$ and correspond to the same arc $O L$. Hence $$ \hat{A}_{I}=\hat{C}_{1}=\hat{x} $$ From (5) and (6) we have $\hat{A}_{1}=\hat{A}_{2}$, i.e. $A L$ is the bisector of the angle $B \hat{A} O$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="87"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> G4 CYP Let $\triangle A B C$ be an acute triangle. The lines $\left(\varepsilon_{1}\right),\left(\varepsilon_{2}\right)$ are perpendicular to $A B$ at the points $A$, $B$, respectively. The perpendicular lines from the midpoint $M$ of $A B$ to the sides of the triangle $A C_{;} B C$ intersect the lines $\left(\varepsilon_{1}\right),\left(\xi_{2}\right)$ at the points $E, F$, respectively. If $I$ is the intersection point of $E F, M C$, prove that $$ \angle A I B=\angle E M F=\angle C A B+\angle C B A $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution: Let $H, G$ be the points of intersection of $M E, M F$, with $A C, B C$ respectively. From the similarity of triangles $\triangle M H A$ and $\triangle M A E$ we get $$ \frac{M H}{M A}=\frac{M A}{M E} $$ thus, $M A^{2}=M H \cdot M E$ Similarly, from the similarity of triangles $\triangle M B G$ and $\triangle M F B$ we get $$ \frac{M B}{M F}=\frac{M G}{M B} $$ thus, $M B^{2}=M F \cdot M G$ Since $M A=M B$, from (1), (2), we have that the points $E, H, G, F$ are concyclic. ![](https://cdn.mathpix.com/cropped/2024_06_05_07a1b610f48bd7c35addg-09.jpg?height=710&width=1025&top_left_y=298&top_left_x=298) Therefore, we get that $\angle F E H=\angle F E M=\angle H G M$. Also, the quadrilateral $C H M G$ is cyclic, so $\angle C M H=\angle H G C$. We have $$ \angle F E H+\angle C M H=\angle H G M+\angle H G C=90^{\circ} $$ Thus $C M \perp E F$. Now, from the cyclic quadrilaterals $F I M B$ and EIMA, we get that $\angle I F M=\angle I B M$ and $\angle I E M=\angle I A M$. Therefore, the triangles $\triangle E M F$ and $\triangle A I B$ are similar, so $\angle A J B=\angle E M F$. Finally $$ \angle A I B=\angle A I M+\angle M I B=\angle A E M+\angle M F B=\angle C A B+\angle C B A $$ </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="88"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> G5 ROU Let $A B C$ be an acute triangle with $A B \neq A C$. The incircle $\omega$ of the triangle touches the sides $B C, C A$ and $A B$ at $D, E$ and $F$, respectively. The perpendicular line erected at $C$ onto $B C$ meets $E F$ at $M$, and similarly, the perpendicular line erected at $B$ onto $B C$ meets $E F$ at $N$. The line $D M$ meets $\omega$ again in $P$, and the line $D N$ meets $\omega$ again at $Q$. Prove that $D P=D Q$. ![](https://cdn.mathpix.com/cropped/2024_06_05_07a1b610f48bd7c35addg-09.jpg?height=583&width=737&top_left_y=1595&top_left_x=607) </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution: ## Proof 1.1. Let $\{T\}=E F \cap B C$. Applying Menelaus' theorem to the triangle $A B C$ and the transversal line $E-F-T$ we obtain $\frac{T B}{T C} \cdot \frac{E C}{E A} \cdot \frac{F A}{F B}=1$, i.e. $\frac{T B}{T C} \cdot \frac{s-c}{s-a} \cdot \frac{s-a}{s-b}=1$, or $\frac{T B}{T C}=\frac{s-b}{s-c}$, where the notations are the usual ones. This means that triangles $T B N$ and $T C M$ are similar, therefore $\frac{T B}{T C}=\frac{B N}{C M}$. From the above it follows $\frac{B N}{C M}=\frac{s-b}{s-c}, \frac{B D}{C D}=\frac{s-b}{s-c}$, and $\angle D B N=\angle D C M=90^{\circ}$, which means that triangles $B D N$ and $C D M$ are similar, hence angles $B D N$ and $C D M$ are equal. This leads to the arcs $D Q$ and $D P$ being equal, and finally to $D P=D Q$. ## Proof 1.2. Let $S$ be the meeting point of the altitude from $A$ with the line $E F$. Lines $B N, A S, C M$ are parallel, therefore triangles $B N F$ and $A S F$ are similar, as are triangles $A S E$ and $C M E$. We obtain $\frac{B N}{A S}=\frac{B F}{F A}$ and $\frac{A S}{C M}=\frac{A E}{E C}$. Multiplying the two relations, we obtain $\frac{B N}{C M}=\frac{B F}{F A} \cdot \frac{A E}{E C}=\frac{B F}{E C}=\frac{B D}{D C}$ (we have used that $A E=A F, B F=B D$ and $C E=C D)$. It follows that the right triangles $B D N$ and $C D M$ are similar (SAS), which leads to the same ending as in the first proof. ## NUMBER THEORY </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Geometry</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="89"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> NT1 SAU What is the greatest number of integers that can be selected from a set of 2015 consecutive numbers so that no sum of any two selected numbers is divisible by their difference? </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution: We take any two chosen numbers. If their difference is 1 , it is clear that their sum is divisible by their difference. If their difference is 2 , they will be of the same parity, and their sum is divisible by their difference. Therefore, the difference between any chosen numbers will be at least 3 . In other words, we can choose at most one number of any three consecutive numbers. This implies that we can choose at most 672 numbers. Now, we will show that we can choose 672 such numbers from any 2015 consecutive numbers. Suppose that these numbers are $a, a+1, \ldots, a+2014$. If $a$ is divisible by 3 , we can choose $a+1, a+4, \ldots, a+2014$. If $a$ is not divisible by 3 , we can choose $a, a+3, \ldots, a+$ 2013. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">672</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">math-word-problem</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr><tr class="group cursor-pointer space-x-4 divide-x border-b outline-offset-[-2px] odd:bg-gray-50 hover:bg-gray-100 dark:odd:bg-gray-925 dark:hover:bg-gray-850 last:border-none" tabindex="0" data-row-idx="90"><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto"> NT2 BUL A positive integer is called a repunit, if it is written only by ones. The repunit with $n$ digits will be denoted by $\underbrace{11 \ldots 1}_{n}$. Prove that: a) the repunit $\underbrace{11 \ldots 1}_{n}$ is divisible by 37 if and only if $n$ is divisible by 3 ; b) there exists a positive integer $k$ such that the repunit $\underbrace{11 \ldots 1}_{n}$ is divisible by 41 if and only if $n$ is divisible by $k$. </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">## Solution: a) Let $n=3 m+r$, where $m$ and $r$ are non-negative integers and $r<3$. Denote by $\underbrace{00 \ldots 0}_{p}$ a recording with $p$ zeroes and $\underbrace{a b c a b c \ldots a b c}_{p x a b c c}$ recording with $p$ times $a b c$. We have: $\quad \underbrace{11 \ldots 1}_{n}=\underbrace{11 \ldots 1}_{3 m+r}=\underbrace{11 \ldots 1}_{3 m} \cdot \underbrace{00 \ldots 0}_{r}+\underbrace{11 \ldots 1}_{\tau}=111 \cdot \underbrace{100100 \ldots 100100 \ldots 0}_{(m-1) \times 100}+\underbrace{11 \ldots 1}_{r}$. Since $111=37.3$, the numbers $\underbrace{11 \ldots 1}_{n}$ and $\underbrace{11 \ldots 1}_{r}$ are equal modulo 37 . On the other hand the numbers 1 and 11 are not divisible by 37 . We conclude that $\underbrace{11 \ldots 1}_{n}$ is divisible by 37 if only if $r=0$, i.e. if and only if $n$ is divisible by 3 . b) Using the idea from a), we look for a repunit, which is divisible by 41 . Obviously, 1 and 11 are not divisible by 41 , while the residues of 111 and 1111 are 29 and 4 , respectively. We have $11111=41 \cdot 271$. Since 11111 is a repunit with 5 digits, it follows in the same way as in a) that $\underbrace{1}_{11 \ldots 1}$ is divisible by 41 if and only if $n$ is divisible by 5 . </div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Number Theory</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">proof</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">Yes</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="" dir="auto">olympiads</div></div> </td><td class="min-w-fit max-w-sm break-words p-2 "><div class="line-clamp-2 "><div class="text-right" dir="auto">false</div></div> </td> </tr></tbody></table> <div class="sticky left-0 border-t border-dashed border-gray-300 bg-gradient-to-b from-gray-100 to-white py-3 text-center font-mono text-xs dark:border-gray-700 dark:from-gray-950 dark:to-gray-900">End of preview. <a href="/datasets/AI-MO/NuminaMath-1.5/viewer/default/train" class="group"><span class="underline decoration-gray-300 group-hover:decoration-gray-400 dark:decoration-gray-500 dark:group-hover:decoration-gray-300">Expand</span> in <svg class="text-xs mr-0.5 inline -translate-y-px text-red-500" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 24 24"><path class="uim-primary" d="M21 22H3a1 1 0 0 1-1-1V3a1 1 0 0 1 1-1h18a1 1 0 0 1 1 1v18a1 1 0 0 1-1 1zM4 20h16V4H4z" fill="currentColor"></path><path class="uim-primary" d="M9 22a1 1 0 0 1-1-1V3a1 1 0 0 1 2 0v18a1 1 0 0 1-1 1zm6 0a1 1 0 0 1-1-1V3a1 1 0 0 1 2 0v18a1 1 0 0 1-1 1z" fill="currentColor"></path><path class="uim-primary" d="M21 10H3a1 1 0 0 1 0-2h18a1 1 0 0 1 0 2zm0 6H3a1 1 0 0 1 0-2h18a1 1 0 0 1 0 2z" fill="currentColor"></path></svg>Dataset Viewer. </a></div></div> <div class="bg-gradient-to-b from-gray-100 to-white dark:from-gray-950 dark:to-gray-900"><hr class="flex-none -translate-y-px border-t border-dashed border-gray-300 bg-white dark:border-gray-700 dark:bg-gray-950"> <nav><ul class="flex select-none items-center justify-between space-x-2 text-gray-700 sm:justify-center py-1 text-center font-mono text-xs rounded-b-lg"><li><a class="flex items-center rounded-lg px-2.5 py-1 hover:bg-gray-50 dark:hover:bg-gray-800 pointer-events-none cursor-default text-gray-400 hover:text-gray-700" href=""><svg class="mr-1.5" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32"><path d="M10 16L20 6l1.4 1.4l-8.6 8.6l8.6 8.6L20 26z" fill="currentColor"></path></svg> Previous</a></li> <li class="hidden sm:block"><a class="rounded-lg px-2.5 py-1 bg-gray-50 font-semibold ring-1 ring-inset ring-gray-200 dark:bg-gray-900 dark:text-yellow-500 dark:ring-gray-900 hover:bg-gray-50 dark:hover:bg-gray-800" href="/datasets/AI-MO/NuminaMath-1.5/viewer/default/train?p=0">1</a> </li><li class="hidden sm:block"><a class="rounded-lg px-2.5 py-1 hover:bg-gray-50 dark:hover:bg-gray-800" href="/datasets/AI-MO/NuminaMath-1.5/viewer/default/train?p=1">2</a> </li><li class="hidden sm:block"><a class="rounded-lg px-2.5 py-1 hover:bg-gray-50 dark:hover:bg-gray-800" href="/datasets/AI-MO/NuminaMath-1.5/viewer/default/train?p=2">3</a> </li><li class="hidden sm:block"><a class="rounded-lg px-2.5 py-1 pointer-events-none cursor-default" href="#">...</a> </li><li class="hidden sm:block"><a class="rounded-lg px-2.5 py-1 hover:bg-gray-50 dark:hover:bg-gray-800" href="/datasets/AI-MO/NuminaMath-1.5/viewer/default/train?p=8962">8,963</a> </li> <li><a class="flex items-center rounded-lg px-2.5 py-1 hover:bg-gray-50 dark:hover:bg-gray-800 " href="/datasets/AI-MO/NuminaMath-1.5/viewer/default/train?p=1">Next <svg class="ml-1.5 transform rotate-180" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32"><path d="M10 16L20 6l1.4 1.4l-8.6 8.6l8.6 8.6L20 26z" fill="currentColor"></path></svg></a></li></ul></nav></div></div> </div></div> <div class="SVELTE_HYDRATER contents" data-target="RepoCodeCopy" data-props="{}"><div></div></div> <div class="SVELTE_HYDRATER contents" data-target="SideNavigation" data-props="{"titleTree":[{"id":"dataset-summary","label":"Dataset Summary","children":[],"isValid":true,"title":"Dataset Summary"},{"id":"whats-new","label":"What&#39;s new?","children":[{"id":"problem-metadata","label":"Problem metadata","children":[],"isValid":true,"title":"Problem metadata"},{"id":"some-new-data-more-to-come","label":"Some new data (more to come)","children":[],"isValid":true,"title":"Some new data (more to come)"}],"isValid":true,"title":"What&#39;s new?"},{"id":"source-breakdown","label":"Source breakdown","children":[],"isValid":true,"title":"Source breakdown"},{"id":"licensing-information","label":"Licensing Information","children":[],"isValid":true,"title":"Licensing Information"},{"id":"citation-information","label":"Citation Information","children":[],"isValid":true,"title":"Citation Information"}],"classNames":"top-6"}"> <div class="absolute -left-12 bottom-0 top-0 z-10 top-6"><div class="sticky top-4 flex"><div class="h-7 pt-[0.175rem]"> <span class="peer" tabindex="0"><button class="select-none hover:cursor-pointer"><svg width="1em" height="1em" viewBox="0 0 10 10" class="text-lg opacity-80 hover:opacity-100" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" preserveAspectRatio="xMidYMid meet" fill="currentColor"><path fill-rule="evenodd" clip-rule="evenodd" d="M1.65039 2.9999C1.65039 2.8066 1.80709 2.6499 2.00039 2.6499H8.00039C8.19369 2.6499 8.35039 2.8066 8.35039 2.9999C8.35039 3.1932 8.19369 3.3499 8.00039 3.3499H2.00039C1.80709 3.3499 1.65039 3.1932 1.65039 2.9999ZM1.65039 4.9999C1.65039 4.8066 1.80709 4.6499 2.00039 4.6499H8.00039C8.19369 4.6499 8.35039 4.8066 8.35039 4.9999C8.35039 5.1932 8.19369 5.3499 8.00039 5.3499H2.00039C1.80709 5.3499 1.65039 5.1932 1.65039 4.9999ZM2.00039 6.6499C1.80709 6.6499 1.65039 6.8066 1.65039 6.9999C1.65039 7.1932 1.80709 7.3499 2.00039 7.3499H8.00039C8.19369 7.3499 8.35039 7.1932 8.35039 6.9999C8.35039 6.8066 8.19369 6.6499 8.00039 6.6499H2.00039Z"></path></svg></button></span> <div class="invisible w-0 -translate-x-24 -translate-y-6 overflow-hidden rounded-xl border bg-white transition-transform hover:visible hover:w-52 hover:translate-x-0 peer-focus-within:visible peer-focus-within:w-52 peer-focus-within:translate-x-0"><nav aria-label="Secondary" class="max-h-[550px] overflow-y-auto p-3"><ul><li class="mb-3 text-sm last:mb-0"><a class="mb-1 block break-words font-semibold text-gray-700 hover:underline active:text-gray-900 dark:active:text-gray-200 [&>*]:break-words" href="#dataset-summary" title="Dataset Summary">Dataset Summary</a> <ul class="pl-1"></ul> </li><li class="mb-3 text-sm last:mb-0"><a class="mb-1 block break-words font-semibold text-gray-700 hover:underline active:text-gray-900 dark:active:text-gray-200 [&>*]:break-words" href="#whats-new" title="What&#39;s new?">What's new?</a> <ul class="pl-1"><li><a class="mb-0.5 block break-words hover:underline active:text-gray-700 dark:active:text-gray-300 text-gray-500" href="#problem-metadata" title="Problem metadata">Problem metadata</a> <ul class="pl-2"></ul> </li><li><a class="mb-0.5 block break-words hover:underline active:text-gray-700 dark:active:text-gray-300 text-gray-500" href="#some-new-data-more-to-come" title="Some new data (more to come)">Some new data (more to come)</a> <ul class="pl-2"></ul> </li></ul> </li><li class="mb-3 text-sm last:mb-0"><a class="mb-1 block break-words font-semibold text-gray-700 hover:underline active:text-gray-900 dark:active:text-gray-200 [&>*]:break-words" href="#source-breakdown" title="Source breakdown">Source breakdown</a> <ul class="pl-1"></ul> </li><li class="mb-3 text-sm last:mb-0"><a class="mb-1 block break-words font-semibold text-gray-700 hover:underline active:text-gray-900 dark:active:text-gray-200 [&>*]:break-words" href="#licensing-information" title="Licensing Information">Licensing Information</a> <ul class="pl-1"></ul> </li><li class="mb-3 text-sm last:mb-0"><a class="mb-1 block break-words font-semibold text-gray-700 hover:underline active:text-gray-900 dark:active:text-gray-200 [&>*]:break-words" href="#citation-information" title="Citation Information">Citation Information</a> <ul class="pl-1"></ul> </li></ul></nav></div></div></div></div></div> <div class="2xl:pr-6"><div class="prose pl-6 -ml-6 hf-sanitized hf-sanitized-NxL0NEJswSUPR7AkzsdDU"> <h1 class="relative group flex items-center"> <a rel="nofollow" href="#dataset-card-for-numinamath-15" class="block pr-1.5 text-lg md:absolute md:p-1.5 md:opacity-0 md:group-hover:opacity-100 md:right-full" id="dataset-card-for-numinamath-15"> <span class="header-link"><svg viewBox="0 0 256 256" preserveAspectRatio="xMidYMid meet" height="1em" width="1em" role="img" aria-hidden="true" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns="http://www.w3.org/2000/svg" class="text-gray-500 hover:text-black dark:hover:text-gray-200 w-4"><path fill="currentColor" d="M167.594 88.393a8.001 8.001 0 0 1 0 11.314l-67.882 67.882a8 8 0 1 1-11.314-11.315l67.882-67.881a8.003 8.003 0 0 1 11.314 0zm-28.287 84.86l-28.284 28.284a40 40 0 0 1-56.567-56.567l28.284-28.284a8 8 0 0 0-11.315-11.315l-28.284 28.284a56 56 0 0 0 79.196 79.197l28.285-28.285a8 8 0 1 0-11.315-11.314zM212.852 43.14a56.002 56.002 0 0 0-79.196 0l-28.284 28.284a8 8 0 1 0 11.314 11.314l28.284-28.284a40 40 0 0 1 56.568 56.567l-28.285 28.285a8 8 0 0 0 11.315 11.314l28.284-28.284a56.065 56.065 0 0 0 0-79.196z"></path></svg></span> </a> <span> Dataset Card for NuminaMath 1.5 </span> </h1> <h3 class="relative group flex items-center"> <a rel="nofollow" href="#dataset-summary" class="block pr-1.5 text-lg md:absolute md:p-1.5 md:opacity-0 md:group-hover:opacity-100 md:right-full" id="dataset-summary"> <span class="header-link"><svg viewBox="0 0 256 256" preserveAspectRatio="xMidYMid meet" height="1em" width="1em" role="img" aria-hidden="true" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns="http://www.w3.org/2000/svg" class="text-gray-500 hover:text-black dark:hover:text-gray-200 w-4"><path fill="currentColor" d="M167.594 88.393a8.001 8.001 0 0 1 0 11.314l-67.882 67.882a8 8 0 1 1-11.314-11.315l67.882-67.881a8.003 8.003 0 0 1 11.314 0zm-28.287 84.86l-28.284 28.284a40 40 0 0 1-56.567-56.567l28.284-28.284a8 8 0 0 0-11.315-11.315l-28.284 28.284a56 56 0 0 0 79.196 79.197l28.285-28.285a8 8 0 1 0-11.315-11.314zM212.852 43.14a56.002 56.002 0 0 0-79.196 0l-28.284 28.284a8 8 0 1 0 11.314 11.314l28.284-28.284a40 40 0 0 1 56.568 56.567l-28.285 28.285a8 8 0 0 0 11.315 11.314l28.284-28.284a56.065 56.065 0 0 0 0-79.196z"></path></svg></span> </a> <span> Dataset Summary </span> </h3> <p>This is the second iteration of the popular <a rel="nofollow" href="https://huggingface.co/datasets/AI-MO/NuminaMath-CoT">NuminaMath</a> dataset, bringing high quality post-training data for approximately 900k competition-level math problems. Each solution is formatted in a Chain of Thought (CoT) manner. The sources of the dataset range from Chinese high school math exercises to US and international mathematics olympiad competition problems. The data were primarily collected from online exam paper PDFs and mathematics discussion forums.</p> <h3 class="relative group flex items-center"> <a rel="nofollow" href="#whats-new" class="block pr-1.5 text-lg md:absolute md:p-1.5 md:opacity-0 md:group-hover:opacity-100 md:right-full" id="whats-new"> <span class="header-link"><svg viewBox="0 0 256 256" preserveAspectRatio="xMidYMid meet" height="1em" width="1em" role="img" aria-hidden="true" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns="http://www.w3.org/2000/svg" class="text-gray-500 hover:text-black dark:hover:text-gray-200 w-4"><path fill="currentColor" d="M167.594 88.393a8.001 8.001 0 0 1 0 11.314l-67.882 67.882a8 8 0 1 1-11.314-11.315l67.882-67.881a8.003 8.003 0 0 1 11.314 0zm-28.287 84.86l-28.284 28.284a40 40 0 0 1-56.567-56.567l28.284-28.284a8 8 0 0 0-11.315-11.315l-28.284 28.284a56 56 0 0 0 79.196 79.197l28.285-28.285a8 8 0 1 0-11.315-11.314zM212.852 43.14a56.002 56.002 0 0 0-79.196 0l-28.284 28.284a8 8 0 1 0 11.314 11.314l28.284-28.284a40 40 0 0 1 56.568 56.567l-28.285 28.285a8 8 0 0 0 11.315 11.314l28.284-28.284a56.065 56.065 0 0 0 0-79.196z"></path></svg></span> </a> <span> What's new? </span> </h3> <h4 class="relative group flex items-center"> <a rel="nofollow" href="#problem-metadata" class="block pr-1.5 text-lg md:absolute md:p-1.5 md:opacity-0 md:group-hover:opacity-100 md:right-full" id="problem-metadata"> <span class="header-link"><svg viewBox="0 0 256 256" preserveAspectRatio="xMidYMid meet" height="1em" width="1em" role="img" aria-hidden="true" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns="http://www.w3.org/2000/svg" class="text-gray-500 hover:text-black dark:hover:text-gray-200 w-4"><path fill="currentColor" d="M167.594 88.393a8.001 8.001 0 0 1 0 11.314l-67.882 67.882a8 8 0 1 1-11.314-11.315l67.882-67.881a8.003 8.003 0 0 1 11.314 0zm-28.287 84.86l-28.284 28.284a40 40 0 0 1-56.567-56.567l28.284-28.284a8 8 0 0 0-11.315-11.315l-28.284 28.284a56 56 0 0 0 79.196 79.197l28.285-28.285a8 8 0 1 0-11.315-11.314zM212.852 43.14a56.002 56.002 0 0 0-79.196 0l-28.284 28.284a8 8 0 1 0 11.314 11.314l28.284-28.284a40 40 0 0 1 56.568 56.567l-28.285 28.285a8 8 0 0 0 11.315 11.314l28.284-28.284a56.065 56.065 0 0 0 0-79.196z"></path></svg></span> </a> <span> Problem metadata </span> </h4> <p>After understanding the importance of verifiable output for each problem, we have added <code>answer</code>, <code>problem_type</code>, <code>question_type</code> metadata for all problems:</p> <ul> <li><code>answer</code>: Final answer of the problem when <code>question_type</code> is a "math word problem", i.e. a number-valued output. For problems which do not belong to this category, <code>answer</code> takes one of the following special values:<ul> <li><code>proof</code>: When the <code>question_type</code> is proof</li> <li><code>notfound</code>: When we cannot find the answer from the <code>ref_solution</code></li> </ul> </li> <li><code>problem_type</code>: The mathematical domain of the problem. See <code>find_problem_type</code> for more information. Here are the supported types:<ul> <li>Algebra</li> <li>Geometry</li> <li>Number Theory</li> <li>Combinatorics</li> <li>Calculus</li> <li>Inequalities</li> <li>Logic and Puzzles</li> <li>Other</li> </ul> </li> <li><code>question_type</code>: The form or style of the mathematical problem.<ul> <li>multiple-choice question (MCQ)</li> <li>proof</li> <li>math-word-problem (problem with output)</li> </ul> </li> </ul> <h4 class="relative group flex items-center"> <a rel="nofollow" href="#some-new-data-more-to-come" class="block pr-1.5 text-lg md:absolute md:p-1.5 md:opacity-0 md:group-hover:opacity-100 md:right-full" id="some-new-data-more-to-come"> <span class="header-link"><svg viewBox="0 0 256 256" preserveAspectRatio="xMidYMid meet" height="1em" width="1em" role="img" aria-hidden="true" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns="http://www.w3.org/2000/svg" class="text-gray-500 hover:text-black dark:hover:text-gray-200 w-4"><path fill="currentColor" d="M167.594 88.393a8.001 8.001 0 0 1 0 11.314l-67.882 67.882a8 8 0 1 1-11.314-11.315l67.882-67.881a8.003 8.003 0 0 1 11.314 0zm-28.287 84.86l-28.284 28.284a40 40 0 0 1-56.567-56.567l28.284-28.284a8 8 0 0 0-11.315-11.315l-28.284 28.284a56 56 0 0 0 79.196 79.197l28.285-28.285a8 8 0 1 0-11.315-11.314zM212.852 43.14a56.002 56.002 0 0 0-79.196 0l-28.284 28.284a8 8 0 1 0 11.314 11.314l28.284-28.284a40 40 0 0 1 56.568 56.567l-28.285 28.285a8 8 0 0 0 11.315 11.314l28.284-28.284a56.065 56.065 0 0 0 0-79.196z"></path></svg></span> </a> <span> Some new data (more to come) </span> </h4> <ul> <li>Olympiads Reference (source: olympiads ref). After the publication of the first <a rel="nofollow" href="https://huggingface.co/datasets/AI-MO/NuminaMath-CoT">NuminaMath</a> dataset, we realized that there are a lot of parsing issues with the <code>olympiads</code> subset, due to the use of generic regular experessions and LLMs. To fix this, we have used the official websites from dozens of national Math Olympiads to perform manual parsing and verification of the problems and solutions.</li> <li>More manual curated data. <code>cn_contest</code>, <code>inequalities</code> and <code>number_theory</code> are manually curated competition problems provided by our data partners.</li> <li>Removal of synthetic dataset <code>synthetic_amc</code>. In our ablation study, this hurt a bit the performance. In the futhur we planned to remove all synthetic data until we find a way to reliably generate high-quality synthetic problems.</li> </ul> <h3 class="relative group flex items-center"> <a rel="nofollow" href="#source-breakdown" class="block pr-1.5 text-lg md:absolute md:p-1.5 md:opacity-0 md:group-hover:opacity-100 md:right-full" id="source-breakdown"> <span class="header-link"><svg viewBox="0 0 256 256" preserveAspectRatio="xMidYMid meet" height="1em" width="1em" role="img" aria-hidden="true" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns="http://www.w3.org/2000/svg" class="text-gray-500 hover:text-black dark:hover:text-gray-200 w-4"><path fill="currentColor" d="M167.594 88.393a8.001 8.001 0 0 1 0 11.314l-67.882 67.882a8 8 0 1 1-11.314-11.315l67.882-67.881a8.003 8.003 0 0 1 11.314 0zm-28.287 84.86l-28.284 28.284a40 40 0 0 1-56.567-56.567l28.284-28.284a8 8 0 0 0-11.315-11.315l-28.284 28.284a56 56 0 0 0 79.196 79.197l28.285-28.285a8 8 0 1 0-11.315-11.314zM212.852 43.14a56.002 56.002 0 0 0-79.196 0l-28.284 28.284a8 8 0 1 0 11.314 11.314l28.284-28.284a40 40 0 0 1 56.568 56.567l-28.285 28.285a8 8 0 0 0 11.315 11.314l28.284-28.284a56.065 56.065 0 0 0 0-79.196z"></path></svg></span> </a> <span> Source breakdown </span> </h3> <div class="max-w-full overflow-auto"> <table> <thead><tr> <th align="left">source</th> <th align="right">problems</th> <th align="right">question_type:proof</th> <th align="right">question_type:mcq</th> <th align="right">question_type:word</th> </tr> </thead><tbody><tr> <td align="left">olympiads</td> <td align="right">197084</td> <td align="right">62970</td> <td align="right">13529</td> <td align="right">117845</td> </tr> <tr> <td align="left">olympiads_ref</td> <td align="right">3638</td> <td align="right">2246</td> <td align="right">nan</td> <td align="right">1392</td> </tr> <tr> <td align="left">amc_aime</td> <td align="right">5872</td> <td align="right">208</td> <td align="right">4374</td> <td align="right">963</td> </tr> <tr> <td align="left">aops_forum</td> <td align="right">67841</td> <td align="right">24532</td> <td align="right">5924</td> <td align="right">33486</td> </tr> <tr> <td align="left">cn_contest</td> <td align="right">29944</td> <td align="right">8663</td> <td align="right">5602</td> <td align="right">15649</td> </tr> <tr> <td align="left">inequalities</td> <td align="right">7314</td> <td align="right">5780</td> <td align="right">49</td> <td align="right">1478</td> </tr> <tr> <td align="left">number_theory</td> <td align="right">4043</td> <td align="right">2591</td> <td align="right">15</td> <td align="right">1239</td> </tr> <tr> <td align="left">cn_k12</td> <td align="right">268819</td> <td align="right">3966</td> <td align="right">115800</td> <td align="right">149010</td> </tr> <tr> <td align="left">orca_math</td> <td align="right">151934</td> <td align="right">1</td> <td align="right">17</td> <td align="right">151916</td> </tr> <tr> <td align="left">synthetic_math</td> <td align="right">148712</td> <td align="right">41</td> <td align="right">1057</td> <td align="right">147612</td> </tr> <tr> <td align="left">metamath</td> <td align="right">11014</td> <td align="right">nan</td> <td align="right">82</td> <td align="right">10932</td> </tr> <tr> <td align="left">Total</td> <td align="right">896215</td> <td align="right">110998</td> <td align="right">146449</td> <td align="right">631522</td> </tr> </tbody> </table> </div> <h3 class="relative group flex items-center"> <a rel="nofollow" href="#licensing-information" class="block pr-1.5 text-lg md:absolute md:p-1.5 md:opacity-0 md:group-hover:opacity-100 md:right-full" id="licensing-information"> <span class="header-link"><svg viewBox="0 0 256 256" preserveAspectRatio="xMidYMid meet" height="1em" width="1em" role="img" aria-hidden="true" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns="http://www.w3.org/2000/svg" class="text-gray-500 hover:text-black dark:hover:text-gray-200 w-4"><path fill="currentColor" d="M167.594 88.393a8.001 8.001 0 0 1 0 11.314l-67.882 67.882a8 8 0 1 1-11.314-11.315l67.882-67.881a8.003 8.003 0 0 1 11.314 0zm-28.287 84.86l-28.284 28.284a40 40 0 0 1-56.567-56.567l28.284-28.284a8 8 0 0 0-11.315-11.315l-28.284 28.284a56 56 0 0 0 79.196 79.197l28.285-28.285a8 8 0 1 0-11.315-11.314zM212.852 43.14a56.002 56.002 0 0 0-79.196 0l-28.284 28.284a8 8 0 1 0 11.314 11.314l28.284-28.284a40 40 0 0 1 56.568 56.567l-28.285 28.285a8 8 0 0 0 11.315 11.314l28.284-28.284a56.065 56.065 0 0 0 0-79.196z"></path></svg></span> </a> <span> Licensing Information </span> </h3> <p>The dataset is available under the <a rel="nofollow" href="https://www.apache.org/licenses/LICENSE-2.0">Apache License, Version 2.0</a>.</p> <h3 class="relative group flex items-center"> <a rel="nofollow" href="#citation-information" class="block pr-1.5 text-lg md:absolute md:p-1.5 md:opacity-0 md:group-hover:opacity-100 md:right-full" id="citation-information"> <span class="header-link"><svg viewBox="0 0 256 256" preserveAspectRatio="xMidYMid meet" height="1em" width="1em" role="img" aria-hidden="true" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns="http://www.w3.org/2000/svg" class="text-gray-500 hover:text-black dark:hover:text-gray-200 w-4"><path fill="currentColor" d="M167.594 88.393a8.001 8.001 0 0 1 0 11.314l-67.882 67.882a8 8 0 1 1-11.314-11.315l67.882-67.881a8.003 8.003 0 0 1 11.314 0zm-28.287 84.86l-28.284 28.284a40 40 0 0 1-56.567-56.567l28.284-28.284a8 8 0 0 0-11.315-11.315l-28.284 28.284a56 56 0 0 0 79.196 79.197l28.285-28.285a8 8 0 1 0-11.315-11.314zM212.852 43.14a56.002 56.002 0 0 0-79.196 0l-28.284 28.284a8 8 0 1 0 11.314 11.314l28.284-28.284a40 40 0 0 1 56.568 56.567l-28.285 28.285a8 8 0 0 0 11.315 11.314l28.284-28.284a56.065 56.065 0 0 0 0-79.196z"></path></svg></span> </a> <span> Citation Information </span> </h3> <pre><code>@misc{numina_math_datasets, author = {Jia LI and Edward Beeching and Lewis Tunstall and Ben Lipkin and Roman Soletskyi and Shengyi Costa Huang and Kashif Rasul and Longhui Yu and Albert Jiang and Ziju Shen and Zihan Qin and Bin Dong and Li Zhou and Yann Fleureau and Guillaume Lample and Stanislas Polu}, title = {NuminaMath}, year = {2024}, publisher = {Numina}, journal = {Hugging Face repository}, howpublished = {\url{[https://huggingface.co/AI-MO/NuminaMath-1.5](https://github.com/project-numina/aimo-progress-prize/blob/main/report/numina_dataset.pdf)}} } </code></pre> </div> </div></section> <section class="pt-6 border-gray-100 md:pb-24 md:pl-6 md:w-64 lg:w-80 xl:w-96 flex-none order-first md:order-none md:border-l !pt-3 md:!pt-6"><dl class="flex items-baseline justify-between"><dt class="text-sm text-gray-500">Downloads last month</dt><div class="mx-4 flex-1 border-b border-dotted"></div><dd class="font-semibold">1,853</dd></dl> <div class="divider-column-vertical"></div> <div class="grid grid-cols-2 gap-x-2 md:flex md:flex-row md:flex-wrap"><div class="SVELTE_HYDRATER contents" data-target="DatasetAndModelActionsDropdown" data-props="{"classNames":"order-last","discussionsDisabled":false,"repo":{"type":"dataset","name":"AI-MO/NuminaMath-1.5"},"canWrite":false,"canDisable":false,"repoIsPrivate":false,"repoIsGated":false,"repoIsDisabled":false,"repoIsAdminFlaggedNFAA":false,"repoHasBlockedOids":false}"><div class="order-last"><div class="relative "> <button class="btn px-1.5 py-1.5 " type="button"> <svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" role="img" class="p-0.5" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32"><circle cx="16" cy="7" r="3" fill="currentColor"></circle><circle cx="16" cy="16" r="3" fill="currentColor"></circle><circle cx="16" cy="25" r="3" fill="currentColor"></circle></svg> </button> </div></div> </div> <div class="SVELTE_HYDRATER contents" data-target="DatasetLibrary" data-props="{"classNames":"md:w-full xl:w-auto xl:flex-none","libraries":[{"language":"python","library":"datasets","function":"load_dataset","loading_codes":[{"config_name":"default","arguments":{},"code":"from datasets import load_dataset\n\n# Login using e.g. `huggingface-cli login` to access this dataset\nds = load_dataset(\"AI-MO/NuminaMath-1.5\")"}]},{"language":"python","library":"dask","function":"dd.read_parquet","loading_codes":[{"config_name":"default","arguments":{"splits":{"train":"data/train-*-of-*.parquet"}},"code":"import dask.dataframe as dd\n\n# Login using e.g. `huggingface-cli login` to access this dataset\ndf = dd.read_parquet(\"hf://datasets/AI-MO/NuminaMath-1.5/data/train-*-of-*.parquet\")"}]},{"language":"python","library":"mlcroissant","function":"Dataset","loading_codes":[{"config_name":"default","arguments":{"record_set":"default","partial":false},"code":"import requests\nfrom huggingface_hub.file_download import build_hf_headers\nfrom mlcroissant import Dataset\n\n# Login using e.g. `huggingface-cli login` to access this dataset\nheaders = build_hf_headers() # handles authentication\njsonld = requests.get(\"https://huggingface.co/api/datasets/AI-MO/NuminaMath-1.5/croissant\", headers=headers).json()\nds = Dataset(jsonld=jsonld)\nrecords = ds.records(\"default\")"}]},{"language":"python","library":"polars","function":"pl.read_parquet","loading_codes":[{"config_name":"default","arguments":{"splits":{"train":"data/train-*-of-*.parquet"}},"code":"import polars as pl\n\n# Login using e.g. `huggingface-cli login` to access this dataset\ndf = pl.read_parquet('hf://datasets/AI-MO/NuminaMath-1.5/data/train-*-of-*.parquet')\n"}]}]}"><div class="relative md:w-full xl:w-auto xl:flex-none"> <button class="!from-gray-800 max-xl:mb-2 !to-black !text-white !gap-1 !border-gray-800 dark:!border-gray-900 btn w-full cursor-pointer text-sm" type="button"> <svg class="mr-1.5 !mr-0.5 " xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32" style="transform: rotate(360deg);"><path d="M31 16l-7 7l-1.41-1.41L28.17 16l-5.58-5.59L24 9l7 7z" fill="currentColor"></path><path d="M1 16l7-7l1.41 1.41L3.83 16l5.58 5.59L8 23l-7-7z" fill="currentColor"></path><path d="M12.419 25.484L17.639 6l1.932.518L14.35 26z" fill="currentColor"></path></svg> Use this dataset <svg class="-mr-1 text-gray-500" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 24 24"><path d="M16.293 9.293L12 13.586L7.707 9.293l-1.414 1.414L12 16.414l5.707-5.707z" fill="currentColor"></path></svg></button> </div> </div> </div> <div class="divider-column-vertical"></div> <div class="flex flex-col flex-wrap xl:flex-row"><a class="group mb-1.5 flex max-w-full flex-col overflow-hidden rounded-lg border border-gray-100 bg-gradient-to-r from-white via-white to-white px-2 py-1 hover:from-gray-50 dark:from-gray-900 dark:to-gray-925 dark:hover:to-gray-900 md:mr-1.5 " href="https://projectnumina.ai" rel="nofollow" target="_blank"><div class="truncate text-xs text-gray-400">Homepage:</div> <div class="truncate text-sm group-hover:underline"> projectnumina.ai</div></a><a class="group mb-1.5 flex max-w-full flex-col overflow-hidden rounded-lg border border-gray-100 bg-gradient-to-r from-white via-white to-white px-2 py-1 hover:from-gray-50 dark:from-gray-900 dark:to-gray-925 dark:hover:to-gray-900 md:mr-1.5 " href="https://github.com/project-numina/aimo-progress-prize/blob/main/report/numina_dataset.pdf" rel="nofollow" target="_blank"><div class="truncate text-xs text-gray-400">Paper:</div> <div class="truncate text-sm group-hover:underline"> github.com</div></a><a class="group mb-1.5 flex max-w-full flex-col overflow-hidden rounded-lg border border-gray-100 bg-gradient-to-r from-white via-white to-white px-2 py-1 hover:from-gray-50 dark:from-gray-900 dark:to-gray-925 dark:hover:to-gray-900 md:mr-1.5 " href="mailto:jia@projectnumina.ai" rel="nofollow" target="_blank"><div class="truncate text-xs text-gray-400">Point of Contact:</div> <div class="truncate text-sm group-hover:underline"> Jia Li</div></a><a class="group mb-1.5 flex max-w-full flex-col overflow-hidden rounded-lg border border-gray-100 bg-gradient-to-r from-white via-white to-white px-2 py-1 hover:from-gray-50 dark:from-gray-900 dark:to-gray-925 dark:hover:to-gray-900 md:mr-1.5 pointer-events-none" rel="nofollow" target="_blank"><div class="truncate text-xs text-gray-400">Size of downloaded dataset files:</div> <div class="truncate text-sm "> 531 MB</div></a><a class="group mb-1.5 flex max-w-full flex-col overflow-hidden rounded-lg border border-gray-100 bg-gradient-to-r from-white via-white to-white px-2 py-1 hover:from-gray-50 dark:from-gray-900 dark:to-gray-925 dark:hover:to-gray-900 md:mr-1.5 " href="/datasets/AI-MO/NuminaMath-1.5/tree/refs%2Fconvert%2Fparquet/" rel="nofollow" target="_blank"><div class="truncate text-xs text-gray-400">Size of the auto-converted Parquet files:</div> <div class="truncate text-sm group-hover:underline"> 531 MB</div></a><a class="group mb-1.5 flex max-w-full flex-col overflow-hidden rounded-lg border border-gray-100 bg-gradient-to-r from-white via-white to-white px-2 py-1 hover:from-gray-50 dark:from-gray-900 dark:to-gray-925 dark:hover:to-gray-900 md:mr-1.5 pointer-events-none" rel="nofollow" target="_blank"><div class="truncate text-xs text-gray-400">Number of rows:</div> <div class="truncate text-sm "> 896,215</div></a></div> <div class="divider-column-vertical"></div> <h2 class="mb-5 flex items-baseline overflow-hidden whitespace-nowrap text-smd font-semibold text-gray-800"><svg class="mr-1.5 text-sm inline self-center flex-none text-gray-400" style="" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 24 24"><path class="uim-quaternary" d="M20.23 7.24L12 12L3.77 7.24a1.98 1.98 0 0 1 .7-.71L11 2.76c.62-.35 1.38-.35 2 0l6.53 3.77c.29.173.531.418.7.71z" opacity=".25" fill="currentColor"></path><path class="uim-tertiary" d="M12 12v9.5a2.09 2.09 0 0 1-.91-.21L4.5 17.48a2.003 2.003 0 0 1-1-1.73v-7.5a2.06 2.06 0 0 1 .27-1.01L12 12z" opacity=".5" fill="currentColor"></path><path class="uim-primary" d="M20.5 8.25v7.5a2.003 2.003 0 0 1-1 1.73l-6.62 3.82c-.275.13-.576.198-.88.2V12l8.23-4.76c.175.308.268.656.27 1.01z" fill="currentColor"></path></svg> Models trained or fine-tuned on <span class="ml-1 truncate font-mono text-[0.87rem] font-medium">AI-MO/NuminaMath-1.5</span></h2> <div class="space-y-3"><div class=""><article class="overview-card-wrapper group/repo "><a class="flex items-center justify-between gap-4 p-2" href="/mradermacher/Reasoning-Llama-3.1-CoT-RE1-NMT-V3-ORPO-GGUF"><div class="w-full truncate"><header class="flex items-center mb-1" title="mradermacher/Reasoning-Llama-3.1-CoT-RE1-NMT-V3-ORPO-GGUF"><img alt="" class="w-3 h-3 rounded-full mr-1.5 flex-none flex-none" src="/avatars/6b97d30ff0bdb5d5c633ba850af739cd.svg" crossorigin="anonymous"> <h4 class="text-md truncate font-mono text-black dark:group-hover/repo:text-yellow-500 group-hover/repo:text-indigo-600 text-sm">mradermacher/Reasoning-Llama-3.1-CoT-RE1-NMT-V3-ORPO-GGUF</h4> </header> <div class="mr-1 flex items-center overflow-hidden whitespace-nowrap text-sm leading-tight text-gray-400"> <span class="truncate">Updated <time datetime="2025-02-14T11:02:08" title="Fri, 14 Feb 2025 11:02:08 GMT">7 days ago</time></span> <span class="px-1.5 text-gray-300 dark:text-gray-500">• </span> <svg class="flex-none w-3 text-gray-400 mr-0.5" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" viewBox="0 0 32 32"><path fill="currentColor" d="M26 24v4H6v-4H4v4a2 2 0 0 0 2 2h20a2 2 0 0 0 2-2v-4zm0-10l-1.41-1.41L17 20.17V2h-2v18.17l-7.59-7.58L6 14l10 10l10-10z"></path></svg> 681 <span class="px-1.5 text-gray-300 dark:text-gray-500">• </span> <svg class="flex-none w-3 text-gray-400 mr-1" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32" fill="currentColor"><path d="M22.45,6a5.47,5.47,0,0,1,3.91,1.64,5.7,5.7,0,0,1,0,8L16,26.13,5.64,15.64a5.7,5.7,0,0,1,0-8,5.48,5.48,0,0,1,7.82,0L16,10.24l2.53-2.58A5.44,5.44,0,0,1,22.45,6m0-2a7.47,7.47,0,0,0-5.34,2.24L16,7.36,14.89,6.24a7.49,7.49,0,0,0-10.68,0,7.72,7.72,0,0,0,0,10.82L16,29,27.79,17.06a7.72,7.72,0,0,0,0-10.82A7.49,7.49,0,0,0,22.45,4Z"></path></svg> 1 </div></div> </a></article> </div><div class=""><article class="overview-card-wrapper group/repo "><a class="flex items-center justify-between gap-4 p-2" href="/mradermacher/Reasoning-Llama-3.1-CoT-RE1-NMT-V3-ORPO-i1-GGUF"><div class="w-full truncate"><header class="flex items-center mb-1" title="mradermacher/Reasoning-Llama-3.1-CoT-RE1-NMT-V3-ORPO-i1-GGUF"><img alt="" class="w-3 h-3 rounded-full mr-1.5 flex-none flex-none" src="/avatars/6b97d30ff0bdb5d5c633ba850af739cd.svg" crossorigin="anonymous"> <h4 class="text-md truncate font-mono text-black dark:group-hover/repo:text-yellow-500 group-hover/repo:text-indigo-600 text-sm">mradermacher/Reasoning-Llama-3.1-CoT-RE1-NMT-V3-ORPO-i1-GGUF</h4> </header> <div class="mr-1 flex items-center overflow-hidden whitespace-nowrap text-sm leading-tight text-gray-400"> <span class="truncate">Updated <time datetime="2025-02-14T11:07:22" title="Fri, 14 Feb 2025 11:07:22 GMT">7 days ago</time></span> <span class="px-1.5 text-gray-300 dark:text-gray-500">• </span> <svg class="flex-none w-3 text-gray-400 mr-0.5" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" viewBox="0 0 32 32"><path fill="currentColor" d="M26 24v4H6v-4H4v4a2 2 0 0 0 2 2h20a2 2 0 0 0 2-2v-4zm0-10l-1.41-1.41L17 20.17V2h-2v18.17l-7.59-7.58L6 14l10 10l10-10z"></path></svg> 614 </div></div> </a></article> </div><div class=""><article class="overview-card-wrapper group/repo "><a class="flex items-center justify-between gap-4 p-2" href="/mradermacher/ReasoningCore-3B-RE1-V2-i1-GGUF"><div class="w-full truncate"><header class="flex items-center mb-1" title="mradermacher/ReasoningCore-3B-RE1-V2-i1-GGUF"><img alt="" class="w-3 h-3 rounded-full mr-1.5 flex-none flex-none" src="/avatars/6b97d30ff0bdb5d5c633ba850af739cd.svg" crossorigin="anonymous"> <h4 class="text-md truncate font-mono text-black dark:group-hover/repo:text-yellow-500 group-hover/repo:text-indigo-600 text-sm">mradermacher/ReasoningCore-3B-RE1-V2-i1-GGUF</h4> </header> <div class="mr-1 flex items-center overflow-hidden whitespace-nowrap text-sm leading-tight text-gray-400"> <span class="truncate">Updated <time datetime="2025-02-20T05:29:39" title="Thu, 20 Feb 2025 05:29:39 GMT">1 day ago</time></span> <span class="px-1.5 text-gray-300 dark:text-gray-500">• </span> <svg class="flex-none w-3 text-gray-400 mr-0.5" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" viewBox="0 0 32 32"><path fill="currentColor" d="M26 24v4H6v-4H4v4a2 2 0 0 0 2 2h20a2 2 0 0 0 2-2v-4zm0-10l-1.41-1.41L17 20.17V2h-2v18.17l-7.59-7.58L6 14l10 10l10-10z"></path></svg> 574 </div></div> </a></article> </div><div class=""><article class="overview-card-wrapper group/repo "><a class="flex items-center justify-between gap-4 p-2" href="/mradermacher/ReasoningCore-3B-RE1-V2-GGUF"><div class="w-full truncate"><header class="flex items-center mb-1" title="mradermacher/ReasoningCore-3B-RE1-V2-GGUF"><img alt="" class="w-3 h-3 rounded-full mr-1.5 flex-none flex-none" src="/avatars/6b97d30ff0bdb5d5c633ba850af739cd.svg" crossorigin="anonymous"> <h4 class="text-md truncate font-mono text-black dark:group-hover/repo:text-yellow-500 group-hover/repo:text-indigo-600 text-sm">mradermacher/ReasoningCore-3B-RE1-V2-GGUF</h4> </header> <div class="mr-1 flex items-center overflow-hidden whitespace-nowrap text-sm leading-tight text-gray-400"> <span class="truncate">Updated <time datetime="2025-02-20T05:29:39" title="Thu, 20 Feb 2025 05:29:39 GMT">1 day ago</time></span> <span class="px-1.5 text-gray-300 dark:text-gray-500">• </span> <svg class="flex-none w-3 text-gray-400 mr-0.5" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" viewBox="0 0 32 32"><path fill="currentColor" d="M26 24v4H6v-4H4v4a2 2 0 0 0 2 2h20a2 2 0 0 0 2-2v-4zm0-10l-1.41-1.41L17 20.17V2h-2v18.17l-7.59-7.58L6 14l10 10l10-10z"></path></svg> 320 </div></div> </a></article> </div><div class="hidden md:block"><article class="overview-card-wrapper group/repo "><a class="flex items-center justify-between gap-4 p-2" href="/EpistemeAI/ReasoningCore-3B-RE1-V2"><div class="w-full truncate"><header class="flex items-center mb-1" title="EpistemeAI/ReasoningCore-3B-RE1-V2"><img alt="" class="w-3 h-3 rounded-sm mr-1.5 flex-none flex-none" src="https://cdn-avatars.huggingface.co/v1/production/uploads/651def66d0656f67a5f431b4/4i0EImglFNnczoBhZ7jQM.jpeg" crossorigin="anonymous"> <h4 class="text-md truncate font-mono text-black dark:group-hover/repo:text-yellow-500 group-hover/repo:text-indigo-600 text-sm">EpistemeAI/ReasoningCore-3B-RE1-V2</h4> </header> <div class="mr-1 flex items-center overflow-hidden whitespace-nowrap text-sm leading-tight text-gray-400"><svg class="mr-1.5 text-[.8rem] flex-none" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" fill="currentColor" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 18 18"><path d="M16.2607 8.08202L14.468 6.28928C14.3063 6.12804 14.0873 6.03749 13.859 6.03749C13.6307 6.03749 13.4117 6.12804 13.25 6.28928L5.6375 13.904V16.9125H8.64607L16.2607 9.30002C16.422 9.13836 16.5125 8.91935 16.5125 8.69102C16.5125 8.4627 16.422 8.24369 16.2607 8.08202V8.08202ZM8.1953 15.825H6.725V14.3547L11.858 9.22118L13.3288 10.6915L8.1953 15.825ZM14.0982 9.92262L12.6279 8.45232L13.8606 7.21964L15.3309 8.68994L14.0982 9.92262Z"></path><path d="M6.18125 9.84373H7.26875V6.03748H8.9V4.94998H4.55V6.03748H6.18125V9.84373Z"></path><path d="M4.55 11.475H2.375V2.775H11.075V4.95H12.1625V2.775C12.1625 2.48658 12.0479 2.20997 11.844 2.00602C11.64 1.80208 11.3634 1.6875 11.075 1.6875H2.375C2.08658 1.6875 1.80997 1.80208 1.60602 2.00602C1.40207 2.20997 1.2875 2.48658 1.2875 2.775V11.475C1.2875 11.7634 1.40207 12.04 1.60602 12.244C1.80997 12.4479 2.08658 12.5625 2.375 12.5625H4.55V11.475Z"></path></svg> Text Generation <span class="px-1.5 text-gray-300 dark:text-gray-500">• </span> <span class="truncate">Updated <time datetime="2025-02-19T01:30:06" title="Wed, 19 Feb 2025 01:30:06 GMT">3 days ago</time></span> <span class="px-1.5 text-gray-300 dark:text-gray-500">• </span> <svg class="flex-none w-3 text-gray-400 mr-0.5" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" viewBox="0 0 32 32"><path fill="currentColor" d="M26 24v4H6v-4H4v4a2 2 0 0 0 2 2h20a2 2 0 0 0 2-2v-4zm0-10l-1.41-1.41L17 20.17V2h-2v18.17l-7.59-7.58L6 14l10 10l10-10z"></path></svg> 116 </div></div> </a></article> </div><div class="hidden md:block"><article class="overview-card-wrapper group/repo "><a class="flex items-center justify-between gap-4 p-2" href="/EpistemeAI/Reasoning-Llama-3.1-CoT-RE1-NMT-V3-ORPO"><div class="w-full truncate"><header class="flex items-center mb-1" title="EpistemeAI/Reasoning-Llama-3.1-CoT-RE1-NMT-V3-ORPO"><img alt="" class="w-3 h-3 rounded-sm mr-1.5 flex-none flex-none" src="https://cdn-avatars.huggingface.co/v1/production/uploads/651def66d0656f67a5f431b4/4i0EImglFNnczoBhZ7jQM.jpeg" crossorigin="anonymous"> <h4 class="text-md truncate font-mono text-black dark:group-hover/repo:text-yellow-500 group-hover/repo:text-indigo-600 text-sm">EpistemeAI/Reasoning-Llama-3.1-CoT-RE1-NMT-V3-ORPO</h4> </header> <div class="mr-1 flex items-center overflow-hidden whitespace-nowrap text-sm leading-tight text-gray-400"><svg class="mr-1.5 text-[.8rem] flex-none" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" fill="currentColor" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 18 18"><path d="M16.2607 8.08202L14.468 6.28928C14.3063 6.12804 14.0873 6.03749 13.859 6.03749C13.6307 6.03749 13.4117 6.12804 13.25 6.28928L5.6375 13.904V16.9125H8.64607L16.2607 9.30002C16.422 9.13836 16.5125 8.91935 16.5125 8.69102C16.5125 8.4627 16.422 8.24369 16.2607 8.08202V8.08202ZM8.1953 15.825H6.725V14.3547L11.858 9.22118L13.3288 10.6915L8.1953 15.825ZM14.0982 9.92262L12.6279 8.45232L13.8606 7.21964L15.3309 8.68994L14.0982 9.92262Z"></path><path d="M6.18125 9.84373H7.26875V6.03748H8.9V4.94998H4.55V6.03748H6.18125V9.84373Z"></path><path d="M4.55 11.475H2.375V2.775H11.075V4.95H12.1625V2.775C12.1625 2.48658 12.0479 2.20997 11.844 2.00602C11.64 1.80208 11.3634 1.6875 11.075 1.6875H2.375C2.08658 1.6875 1.80997 1.80208 1.60602 2.00602C1.40207 2.20997 1.2875 2.48658 1.2875 2.775V11.475C1.2875 11.7634 1.40207 12.04 1.60602 12.244C1.80997 12.4479 2.08658 12.5625 2.375 12.5625H4.55V11.475Z"></path></svg> Text Generation <span class="px-1.5 text-gray-300 dark:text-gray-500">• </span> <span class="truncate">Updated <time datetime="2025-02-14T06:37:35" title="Fri, 14 Feb 2025 06:37:35 GMT">7 days ago</time></span> <span class="px-1.5 text-gray-300 dark:text-gray-500">• </span> <svg class="flex-none w-3 text-gray-400 mr-0.5" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" viewBox="0 0 32 32"><path fill="currentColor" d="M26 24v4H6v-4H4v4a2 2 0 0 0 2 2h20a2 2 0 0 0 2-2v-4zm0-10l-1.41-1.41L17 20.17V2h-2v18.17l-7.59-7.58L6 14l10 10l10-10z"></path></svg> 30 <span class="px-1.5 text-gray-300 dark:text-gray-500">• </span> <svg class="flex-none w-3 text-gray-400 mr-1" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32" fill="currentColor"><path d="M22.45,6a5.47,5.47,0,0,1,3.91,1.64,5.7,5.7,0,0,1,0,8L16,26.13,5.64,15.64a5.7,5.7,0,0,1,0-8,5.48,5.48,0,0,1,7.82,0L16,10.24l2.53-2.58A5.44,5.44,0,0,1,22.45,6m0-2a7.47,7.47,0,0,0-5.34,2.24L16,7.36,14.89,6.24a7.49,7.49,0,0,0-10.68,0,7.72,7.72,0,0,0,0,10.82L16,29,27.79,17.06a7.72,7.72,0,0,0,0-10.82A7.49,7.49,0,0,0,22.45,4Z"></path></svg> 1 </div></div> </a></article> </div> </div> <div class="divider-column-vertical"></div> <h2 class="mb-5 flex items-baseline overflow-hidden whitespace-nowrap text-smd font-semibold text-gray-800"><svg class="mr-1 inline self-center flex-none" width="1em" height="1em" aria-hidden="true" focusable="false" role="img" viewBox="0 0 12 13" fill="none" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink"><rect x="2" y="2.49902" width="8" height="3.76425" rx="1.16774" fill="currentColor" fill-opacity="0.4"></rect><rect x="6.21875" y="6.7334" width="3.78055" height="3.76425" rx="1.16774" fill="currentColor" fill-opacity="0.7"></rect><rect x="2" y="6.73438" width="3.78055" height="3.76425" rx="1.16774" fill="currentColor" fill-opacity="0.5"></rect></svg> Collection including <span class="ml-1 truncate font-mono text-[0.86rem] font-medium">AI-MO/NuminaMath-1.5</span></h2> <div class="flex flex-col gap-3"> <div class="flex flex-col"><article class="overview-card-wrapper group/collection relative !rounded-md !from-white !to-white dark:!from-gray-900 dark:!to-gray-900 peer"><a href="/collections/AI-MO/numinamath-6697df380293bcfdbc1d978c" class="block p-2"><header class="mb-0.5 flex items-center" title="NuminaMath"><h4 class="text-md truncate text-smd font-semibold group-hover/collection:underline">NuminaMath</h4> <div class="ml-2 flex items-center rounded sm:ml-2.5 bg-green-500/10 py-0.5 pl-1 pr-1.5 text-xs leading-none text-gray-700"><svg class="mr-0.5 flex-none text-green-700" width="1em" height="1em" aria-hidden="true" focusable="false" role="img" viewBox="0 0 12 13" fill="none" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink"><rect x="2" y="2.49902" width="8" height="3.76425" rx="1.16774" fill="currentColor" fill-opacity="0.4"></rect><rect x="6.21875" y="6.7334" width="3.78055" height="3.76425" rx="1.16774" fill="currentColor" fill-opacity="0.7"></rect><rect x="2" y="6.73438" width="3.78055" height="3.76425" rx="1.16774" fill="currentColor" fill-opacity="0.5"></rect></svg> Collection </div></header> <div class="mr-1 flex items-center overflow-hidden whitespace-nowrap text-sm leading-tight text-gray-400"><span class="max-w-64 truncate">Datasets and models for training SOTA math LLMs. See our GitHub for training & inference code: https://github.com/project-numina/aimo-progress-prize</span> <span class="px-1.5 text-gray-300">• </span> <span>7 items</span> <span class="px-1.5 text-gray-300">• </span> <span class="truncate">Updated <time datetime="2025-02-10T13:39:40" title="2025-02-10T13:39:40.402Z">11 days ago</time></span> <span class="px-1.5 text-gray-300">•</span> <svg class="flex-none w-3 mr-1 text-gray-400" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" aria-hidden="true" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 12 12" fill="transparent"><path d="M9.30013 9.29152H9.3H2.7H2.69987C2.62308 9.29154 2.54762 9.27146 2.481 9.23328C2.41437 9.1951 2.3589 9.14015 2.32009 9.07389C2.28128 9.00763 2.26048 8.93237 2.25977 8.85558C2.25907 8.7798 2.27796 8.70513 2.31458 8.63882L5.62238 2.9426L5.67518 2.85168C5.7059 2.81806 5.74178 2.78928 5.78164 2.76649C5.84813 2.72848 5.9234 2.70848 6 2.70848C6.0766 2.70848 6.15187 2.72848 6.21836 2.76649C6.28441 2.80425 6.33953 2.85848 6.37836 2.92389L9.68527 8.63855C9.72199 8.70493 9.74093 8.7797 9.74023 8.85558C9.73952 8.93237 9.71872 9.00763 9.67991 9.07389C9.6411 9.14015 9.58563 9.1951 9.519 9.23328C9.45238 9.27146 9.37692 9.29154 9.30013 9.29152Z" stroke="currentColor"></path></svg> 75</div></a></article> <div class="overview-card-wrapper -z-1 !rounded-md !bg-gradient-to-t -mt-[1.60rem] h-8 scale-x-[98%] !from-gray-50 !to-gray-50 !shadow-none transition-transform peer-hover:-translate-y-[2px] peer-hover:from-gray-100/80 dark:!from-gray-925 dark:!to-gray-925 dark:peer-hover:from-black"></div></div></div> <div class="divider-column-vertical md:hidden"></div></section></div></main> <footer class="b-12 mb-2 flex border-t border-gray-100 md:h-14"><nav class="container relative flex flex-col justify-between space-y-2 py-6 text-gray-500 *:max-md:self-start md:flex-row md:items-center md:space-y-0 md:py-0 md:text-sm"><div class="SVELTE_HYDRATER contents" data-target="ThemeSwitcher" data-props="{"theme":"system","isLoggedIn":false,"menuClassNames":"md:-top-24","classNames":"max-md:mb-5 *:max-md:self-start"}"> <div class="relative inline-block max-md:mb-5 *:max-md:self-start"> <button class="rounded-full border border-gray-100 pl-2 py-1 pr-2.5 flex items-center text-sm text-gray-500 bg-white hover:bg-purple-50 hover:border-purple-200 dark:hover:bg-gray-800 dark:hover:border-gray-950 dark:border-gray-800 " type="button"> <svg class="mr-1.5 text-gray-500" xmlns="http://www.w3.org/2000/svg" aria-hidden="true" fill="currentColor" focusable="false" role="img" width="1em" height="1em" preserveAspectRatio="xMidYMid meet" viewBox="0 0 32 32"><path d="M29 25H3a1 1 0 1 0 0 2h26a1 1 0 1 0 0-2Z" fill="currentColor"></path><path fill-rule="evenodd" clip-rule="evenodd" d="M6 22.5h20a2 2 0 0 0 2-2V7a2 2 0 0 0-2-2H6a2 2 0 0 0-2 2v13.5a2 2 0 0 0 2 2ZM7 7a1 1 0 0 0-1 1v11a1 1 0 0 0 1 1h18a1 1 0 0 0 1-1V8a1 1 0 0 0-1-1H7Z" fill="currentColor"></path><path d="M6 8a1 1 0 0 1 1-1h18a1 1 0 0 1 1 1v11a1 1 0 0 1-1 1H7a1 1 0 0 1-1-1V8Z" fill="currentColor" fill-opacity=".4"></path><path d="M29 25H3a1 1 0 1 0 0 2h26a1 1 0 1 0 0-2Z" fill="currentColor"></path></svg> System theme </button> </div></div> <div class="font-semibold text-black md:hidden">Company</div> <a class="hover:underline" href="/terms-of-service">TOS</a> <a class="hover:underline" href="/privacy">Privacy</a> <a class="hover:underline" href="/huggingface">About</a> <a class="hover:underline" href="https://apply.workable.com/huggingface/">Jobs</a> <a href="/" class="group flex-none max-md:order-last max-md:!mb-4 max-md:!mt-8"><svg class="h-7 w-7 transition-transform group-hover:-translate-y-px" viewBox="0 0 95 88" fill="none" xmlns="http://www.w3.org/2000/svg"><path d="M47.2119 76.5C66.4037 76.5 81.9619 60.9419 81.9619 41.75C81.9619 22.5581 66.4037 7 47.2119 7C28.02 7 12.4619 22.5581 12.4619 41.75C12.4619 60.9419 28.02 76.5 47.2119 76.5Z" fill="#FFD21E"></path><path d="M81.9619 41.75C81.9619 22.5581 66.4037 7 47.2119 7C28.02 7 12.4619 22.5581 12.4619 41.75C12.4619 60.9419 28.02 76.5 47.2119 76.5C66.4037 76.5 81.9619 60.9419 81.9619 41.75ZM8.46185 41.75C8.46185 20.349 25.8108 3 47.2119 3C68.6129 3 85.9619 20.349 85.9619 41.75C85.9619 63.151 68.6129 80.5 47.2119 80.5C25.8108 80.5 8.46185 63.151 8.46185 41.75Z" fill="#FF9D0B"></path><path d="M58.5024 32.2915C59.7768 32.7415 60.2839 35.3615 61.5713 34.6769C64.0095 33.3805 64.9351 30.353 63.6387 27.9148C62.3423 25.4767 59.3148 24.5511 56.8766 25.8475C54.4384 27.1439 53.5128 30.1714 54.8092 32.6096C55.4211 33.7604 57.3632 31.8892 58.5024 32.2915Z" fill="#3A3B45"></path><path d="M34.9454 32.2915C33.671 32.7415 33.164 35.3615 31.8766 34.6769C29.4384 33.3805 28.5128 30.353 29.8092 27.9148C31.1056 25.4767 34.1331 24.5511 36.5713 25.8475C39.0095 27.1439 39.9351 30.1714 38.6387 32.6096C38.0268 33.7604 36.0846 31.8892 34.9454 32.2915Z" fill="#3A3B45"></path><path d="M46.9619 56.289C56.7903 56.289 59.9619 47.5261 59.9619 43.0262C59.9619 40.6875 58.3898 41.4236 55.8718 42.6702C53.5449 43.8222 50.4102 45.4101 46.9619 45.4101C39.7822 45.4101 33.9619 38.5263 33.9619 43.0262C33.9619 47.5261 37.1334 56.289 46.9619 56.289Z" fill="#3A3B45"></path><mask id="mask0" style="mask-type:alpha" maskUnits="userSpaceOnUse" x="33" y="41" width="27" height="16"><path d="M46.9619 56.289C56.7903 56.289 59.9619 47.5261 59.9619 43.0262C59.9619 40.6875 58.3898 41.4236 55.8718 42.6702C53.5449 43.8222 50.4102 45.4101 46.9619 45.4101C39.7822 45.4101 33.9619 38.5263 33.9619 43.0262C33.9619 47.5261 37.1334 56.289 46.9619 56.289Z" fill="white"></path></mask><g mask="url(#mask0)"><path d="M47.2119 66.5C52.0018 66.5 55.8848 62.617 55.8848 57.8271C55.8848 54.0962 53.5291 50.9156 50.224 49.6915C50.1023 49.6464 49.9794 49.604 49.8553 49.5643C49.0219 49.2979 48.1337 52.1623 47.2119 52.1623C46.3506 52.1623 45.5186 49.2797 44.7332 49.5135C41.151 50.5799 38.5389 53.8984 38.5389 57.8271C38.5389 62.617 42.4219 66.5 47.2119 66.5Z" fill="#F94040"></path></g><path d="M70.7119 37C72.5068 37 73.9619 35.5449 73.9619 33.75C73.9619 31.9551 72.5068 30.5 70.7119 30.5C68.9169 30.5 67.4619 31.9551 67.4619 33.75C67.4619 35.5449 68.9169 37 70.7119 37Z" fill="#FF9D0B"></path><path d="M24.2119 37C26.0068 37 27.4619 35.5449 27.4619 33.75C27.4619 31.9551 26.0068 30.5 24.2119 30.5C22.4169 30.5 20.9619 31.9551 20.9619 33.75C20.9619 35.5449 22.4169 37 24.2119 37Z" fill="#FF9D0B"></path><path class="origin-bottom-right transition-transform group-hover:-rotate-6" d="M17.5238 48C15.9048 48 14.4578 48.665 13.4488 49.871C12.8248 50.618 12.1728 51.822 12.1198 53.625C11.4408 53.43 10.7878 53.321 10.1778 53.321C8.6278 53.321 7.2278 53.915 6.2378 54.994C4.9658 56.379 4.4008 58.081 4.6468 59.784C4.7638 60.595 5.0348 61.322 5.4398 61.995C4.5858 62.686 3.9568 63.648 3.6528 64.805C3.4148 65.712 3.1708 67.601 4.4448 69.547C4.3638 69.674 4.2878 69.806 4.2168 69.941C3.4508 71.395 3.4018 73.038 4.0778 74.568C5.1028 76.887 7.6498 78.714 12.5958 80.675C15.6728 81.895 18.4878 82.675 18.5128 82.682C22.5808 83.737 26.2598 84.273 29.4448 84.273C35.2988 84.273 39.4898 82.48 41.9018 78.944C45.7838 73.25 45.2288 68.042 40.2058 63.022C37.4258 60.244 35.5778 56.148 35.1928 55.249C34.4168 52.587 32.3648 49.628 28.9538 49.628H28.9528C28.6658 49.628 28.3758 49.651 28.0898 49.696C26.5958 49.931 25.2898 50.791 24.3568 52.085C23.3498 50.833 22.3718 49.837 21.4868 49.275C20.1528 48.429 18.8198 48 17.5238 48ZM17.5238 52C18.0338 52 18.6568 52.217 19.3438 52.653C21.4768 54.006 25.5928 61.081 27.0998 63.833C27.6048 64.755 28.4678 65.145 29.2448 65.145C30.7868 65.145 31.9908 63.612 29.3858 61.664C25.4688 58.733 26.8428 53.942 28.7128 53.647C28.7948 53.634 28.8758 53.628 28.9538 53.628C30.6538 53.628 31.4038 56.558 31.4038 56.558C31.4038 56.558 33.6018 62.078 37.3778 65.851C41.1538 69.625 41.3488 72.654 38.5968 76.69C36.7198 79.442 33.1268 80.273 29.4448 80.273C25.6258 80.273 21.7108 79.379 19.5168 78.81C19.4088 78.782 6.0658 75.013 7.7558 71.805C8.0398 71.266 8.5078 71.05 9.0968 71.05C11.4768 71.05 15.8058 74.592 17.6668 74.592C18.0828 74.592 18.3758 74.415 18.4958 73.983C19.2888 71.138 6.4388 69.942 7.5218 65.821C7.7128 65.092 8.2308 64.796 8.9588 64.797C12.1038 64.797 19.1598 70.328 20.6388 70.328C20.7518 70.328 20.8328 70.295 20.8768 70.225C21.6178 69.029 21.2118 68.194 15.9888 65.033C10.7658 61.871 7.0998 59.969 9.1848 57.699C9.4248 57.437 9.7648 57.321 10.1778 57.321C13.3488 57.322 20.8408 64.14 20.8408 64.14C20.8408 64.14 22.8628 66.243 24.0858 66.243C24.3668 66.243 24.6058 66.132 24.7678 65.858C25.6348 64.396 16.7148 57.636 16.2118 54.847C15.8708 52.957 16.4508 52 17.5238 52Z" fill="#FF9D0B"></path><path class="origin-bottom-right transition-transform group-hover:-rotate-6" d="M38.5967 76.6898C41.3487 72.6538 41.1537 69.6248 37.3777 65.8508C33.6017 62.0778 31.4037 56.5578 31.4037 56.5578C31.4037 56.5578 30.5827 53.3518 28.7127 53.6468C26.8427 53.9418 25.4697 58.7328 29.3867 61.6638C33.3037 64.5938 28.6067 66.5848 27.0997 63.8328C25.5927 61.0808 21.4777 54.0058 19.3437 52.6528C17.2107 51.2998 15.7087 52.0578 16.2117 54.8468C16.7147 57.6358 25.6357 64.3958 24.7677 65.8588C23.8997 67.3208 20.8407 64.1398 20.8407 64.1398C20.8407 64.1398 11.2687 55.4288 9.18465 57.6988C7.10065 59.9688 10.7657 61.8708 15.9887 65.0328C21.2127 68.1938 21.6177 69.0288 20.8767 70.2248C20.1347 71.4208 8.60465 61.6998 7.52165 65.8208C6.43965 69.9418 19.2887 71.1378 18.4957 73.9828C17.7027 76.8288 9.44465 68.5978 7.75565 71.8048C6.06565 75.0128 19.4087 78.7818 19.5167 78.8098C23.8267 79.9278 34.7727 82.2968 38.5967 76.6898Z" fill="#FFD21E"></path><path class="origin-bottom-left transition-transform group-hover:rotate-6" d="M77.3999 48C79.0189 48 80.4659 48.665 81.4749 49.871C82.0989 50.618 82.7509 51.822 82.8039 53.625C83.4829 53.43 84.1359 53.321 84.7459 53.321C86.2959 53.321 87.6959 53.915 88.6859 54.994C89.9579 56.379 90.5229 58.081 90.2769 59.784C90.1599 60.595 89.8889 61.322 89.4839 61.995C90.3379 62.686 90.9669 63.648 91.2709 64.805C91.5089 65.712 91.7529 67.601 90.4789 69.547C90.5599 69.674 90.6359 69.806 90.7069 69.941C91.4729 71.395 91.5219 73.038 90.8459 74.568C89.8209 76.887 87.2739 78.714 82.3279 80.675C79.2509 81.895 76.4359 82.675 76.4109 82.682C72.3429 83.737 68.6639 84.273 65.4789 84.273C59.6249 84.273 55.4339 82.48 53.0219 78.944C49.1399 73.25 49.6949 68.042 54.7179 63.022C57.4979 60.244 59.3459 56.148 59.7309 55.249C60.5069 52.587 62.5589 49.628 65.9699 49.628H65.9709C66.2579 49.628 66.5479 49.651 66.8339 49.696C68.3279 49.931 69.6339 50.791 70.5669 52.085C71.5739 50.833 72.5519 49.837 73.4369 49.275C74.7709 48.429 76.1039 48 77.3999 48ZM77.3999 52C76.8899 52 76.2669 52.217 75.5799 52.653C73.4469 54.006 69.3309 61.081 67.8239 63.833C67.3189 64.755 66.4559 65.145 65.6789 65.145C64.1369 65.145 62.9329 63.612 65.5379 61.664C69.4549 58.733 68.0809 53.942 66.2109 53.647C66.1289 53.634 66.0479 53.628 65.9699 53.628C64.2699 53.628 63.5199 56.558 63.5199 56.558C63.5199 56.558 61.3219 62.078 57.5459 65.851C53.7699 69.625 53.5749 72.654 56.3269 76.69C58.2039 79.442 61.7969 80.273 65.4789 80.273C69.2979 80.273 73.2129 79.379 75.4069 78.81C75.5149 78.782 88.8579 75.013 87.1679 71.805C86.8839 71.266 86.4159 71.05 85.8269 71.05C83.4469 71.05 79.1179 74.592 77.2569 74.592C76.8409 74.592 76.5479 74.415 76.4279 73.983C75.6349 71.138 88.4849 69.942 87.4019 65.821C87.2109 65.092 86.6929 64.796 85.9649 64.797C82.8199 64.797 75.7639 70.328 74.2849 70.328C74.1719 70.328 74.0909 70.295 74.0469 70.225C73.3059 69.029 73.7119 68.194 78.9349 65.033C84.1579 61.871 87.8239 59.969 85.7389 57.699C85.4989 57.437 85.1589 57.321 84.7459 57.321C81.5749 57.322 74.0829 64.14 74.0829 64.14C74.0829 64.14 72.0609 66.243 70.8379 66.243C70.5569 66.243 70.3179 66.132 70.1559 65.858C69.2889 64.396 78.2089 57.636 78.7119 54.847C79.0529 52.957 78.4729 52 77.3999 52Z" fill="#FF9D0B"></path><path class="origin-bottom-left transition-transform group-hover:rotate-6" d="M56.3271 76.6898C53.5751 72.6538 53.7701 69.6248 57.5461 65.8508C61.3221 62.0778 63.5201 56.5578 63.5201 56.5578C63.5201 56.5578 64.3411 53.3518 66.2111 53.6468C68.0811 53.9418 69.4541 58.7328 65.5371 61.6638C61.6201 64.5938 66.3171 66.5848 67.8241 63.8328C69.3311 61.0808 73.4461 54.0058 75.5801 52.6528C77.7131 51.2998 79.2151 52.0578 78.7121 54.8468C78.2091 57.6358 69.2881 64.3958 70.1561 65.8588C71.0241 67.3208 74.0831 64.1398 74.0831 64.1398C74.0831 64.1398 83.6551 55.4288 85.7391 57.6988C87.8231 59.9688 84.1581 61.8708 78.9351 65.0328C73.7111 68.1938 73.3061 69.0288 74.0471 70.2248C74.7891 71.4208 86.3191 61.6998 87.4021 65.8208C88.4841 69.9418 75.6351 71.1378 76.4281 73.9828C77.2211 76.8288 85.4791 68.5978 87.1681 71.8048C88.8581 75.0128 75.5151 78.7818 75.4071 78.8098C71.0971 79.9278 60.1511 82.2968 56.3271 76.6898Z" fill="#FFD21E"></path></svg></a> <div class="font-semibold text-black max-md:!mt-8 md:hidden">Website</div> <a class="hover:underline" href="/models">Models</a> <a class="hover:underline" href="/datasets">Datasets</a> <a class="hover:underline" href="/spaces">Spaces</a> <a class="hover:underline" href="/pricing">Pricing</a> <a class="hover:underline" href="/docs">Docs</a></nav></footer></div> <script> import("\/front\/build\/kube-b666922\/index.js"); window.moonSha = "kube-b666922\/"; window.__hf_deferred = {}; </script>  <script> if (["hf.co", "huggingface.co"].includes(window.location.hostname)) { const script = document.createElement("script"); script.src = "https://js.stripe.com/v3/"; script.async = true; document.head.appendChild(script); } </script> </body> </html>